牛客欢乐赛1 D题（动态规划）

Posted 2021-06-15 zjj0624

题意



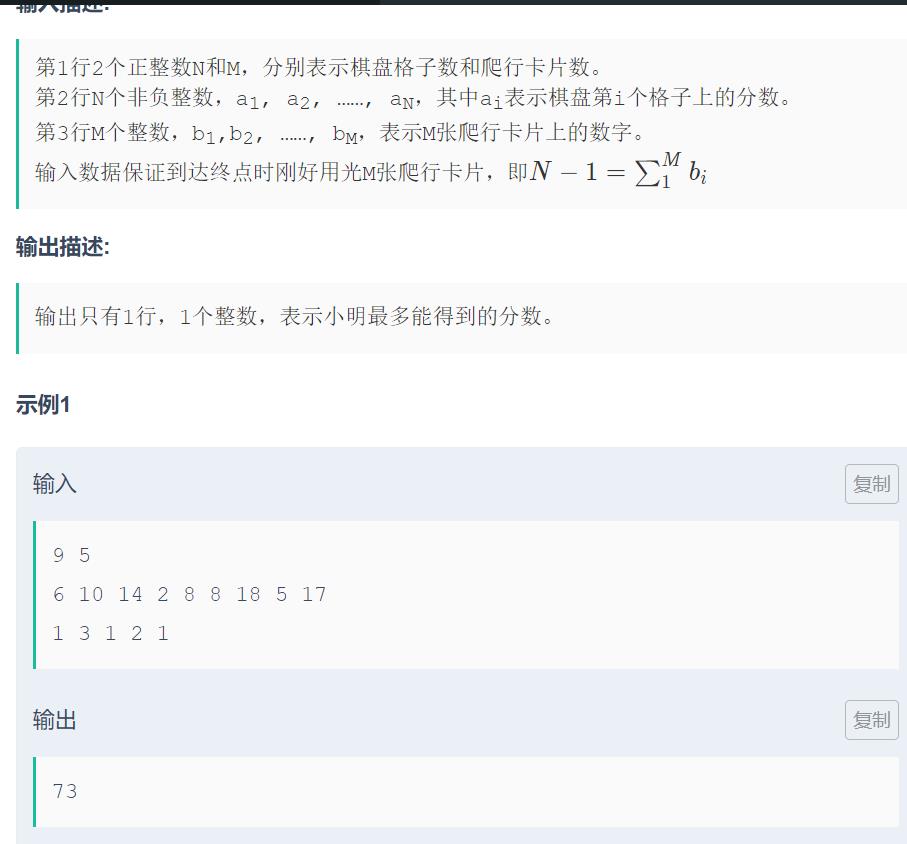
思路
我们看数据范围知道，每一种卡片最多有40张，也就是说这四种卡片的所有情况是$40\ast 40\ast 40\ast 40.$,我们并不好判断每次应该选那个点，我们唯一能知道的就是会经过最后一个点，到达最后一个点一共有四种情况，分别是从n-4到n，n-3到n，n-2到n，n-1到n，这四种情况，这种题一般都是要用到动态规划，用局部最优最后推出全局最优。
$dp[i][j][k][l]$表示已经用了i张1卡片，j张2卡片，k张3卡片，l张4卡片，能得到的最大分数。
转移方程式很好想，就是从四种情况转移过来。

代码

#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
const int N = 1e6;
const int MOD = 1e9+7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
int dp[40][40][40][40];
int a[350];
int size[5];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1 ; i<=n ; i++)
    {
        cin>>a[i];
    }
    for(int i=1 ; i<=m ; i++)
    {
        int x;
        cin>>x;
        size[x]++;
    }
    dp[0][0][0][0]=a[1];
    for(int i=0 ; i<=size[1] ; i++)
    {
        for(int j=0 ; j<=size[2] ; j++)
        {
            for(int k=0 ; k<=size[3] ; k++)
            {
                for(int l=0 ; l<=size[4] ; l++)
                {
                    for(int z=1 ; z<=4 ; z++)
                    {
                        int val=i*1+j*2+k*3+l*4+1;
                        if(z==1) if(i>0) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i-1][j][k][l]+a[val]);
                        if(z==2) if(j>0) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i][j-1][k][l]+a[val]);
                        if(z==3) if(k>0) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i][j][k-1][l]+a[val]);
                        if(z==4) if(l>0) dp[i][j][k][l]=max(dp[i][j][k][l],dp[i][j][k][l-1]+a[val]);
                    }
                    //  cout<<i<<" "<<j<<" "<<k<<" "<<l<<" "<<dp[i][j][k][l]<<endl;
                }
            }
        }
    }
    cout<<dp[size[1]][size[2]][size[3]][size[4]]<<endl;
    return 0;
}