代数47 ----点到平面及直线的距离

Posted 炫云云

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了代数47 ----点到平面及直线的距离相关的知识，希望对你有一定的参考价值。

文章目录

点到平面的距离

设平面 π \\pi π 的方程为 A x + B y + C z + D = 0 A x+B y+C z+D=0 Ax+By+Cz+D=0, 法向量为 n = ( A , B , C ) n=(A, B, C) n=(A,B,C).
取平面 π \\pi π 上的一点 M ( x 1 , y 1 , z 1 ) M\\left(x_{1}, y_{1}, z_{1}\\right) M(x1​,y1​,z1​),
则点 P ( x 0 , y 0 , z 0 ) P\\left(x_{0}, y_{0}, z_{0}\\right) P(x0​,y0​,z0​) 到平面 π \\pi π 的距离为
d = ∣ ( M P → ) n ∣ = ∣ M P → ⋅ n ∣ ∣ n ∣ = ∣ A ( x 0 − x 1 ) + B ( y 0 − y 1 ) + C ( z 0 − z 1 ) ∣ A 2 + B 2 + C 2 d=\\left|(\\overrightarrow{M P})_{n}\\right|=\\frac{|\\overrightarrow{M P} \\cdot \\boldsymbol{n}|}{|\\boldsymbol{n}|}=\\frac{\\left|A\\left(x_{0}-x_{1}\\right)+B\\left(y_{0}-y_{1}\\right)+C\\left(z_{0}-z_{1}\\right)\\right|}{\\sqrt{A^{2}+B^{2}+C^{2}}} d=∣∣∣​(MP )n​∣∣∣​=∣n∣∣MP ⋅n∣​=A2+B2+C2 ​∣A(x0​−x1​)+B(y0​−y1​)+C(z0​−z1​)∣​
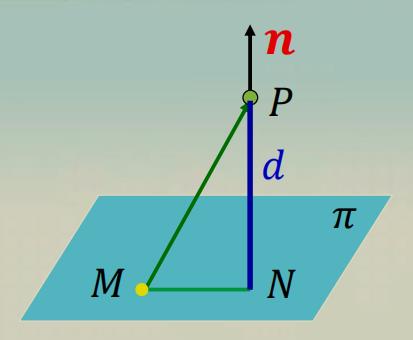
image-20201214122624788

又 A x 1 + B y 1 + C z 1 + D = 0 , A x_{1}+B y_{1}+C z_{1}+D=0, Ax1​+By1​+Cz1​+D=0, 故 d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 \\quad d=\\frac{\\left|A x_{0}+B y_{0}+C z_{0}+D\\right|}{\\sqrt{A^{2}+B^{2}+C^{2}}} d=A2+B2+C2 ​∣Ax0​+By0​+Cz0​+D∣​.

点到平面的距离
d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d=\\frac{\\left|A x_{0}+B y_{0}+C z_{0}+D\\right|}{\\sqrt{A^{2}+B^{2}+C^{2}}} d=A2+B2+C2 ​∣Ax0​+By0​+Cz0​+D∣​
【 注 】 \\Large\\color{violet}{【注】} 【注】可先求出垂足 N N N 的坐标, 再用两点距离公式求 d = ∣ P N ∣ d=|P N| d=∣PN∣.

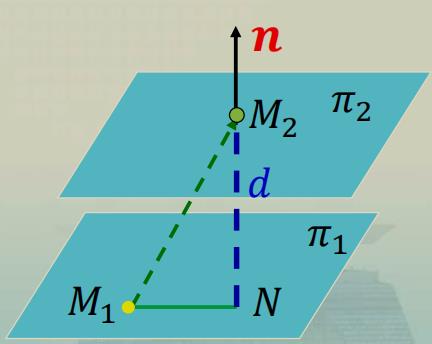
【 注 】 \\Large\\color{violet}{【注】} 【注】两平行平面之间的距离归结为其中
一个平面上任一点到另一平面的距离.

image-20201214122853464

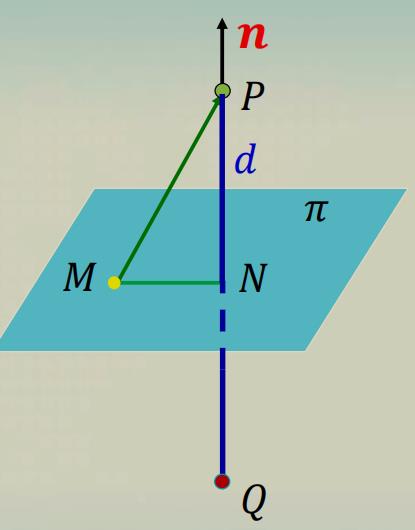
例 1 \\Large\\color{violet}{例1} 例1 求点 P ( 1 , 3 , 2 ) P(1,3,2) P(1,3,2) 到平面 π : 2 x − y − 2 z − 1 = 0 \\pi: 2 x-y-2 z-1=0 π:2x−y−2z−1=0 的距离 d d d
并求点 P P P 关于平面 π \\pi π 的对称点 Q Q Q 的坐标.

image-20201214124833630

【解】 ( 1 ) \\quad(1) (1) 由点到平面的距离公式知
d = ∣ 2 × 1 − 1 × 3 − 2 × 2 − 1 ∣ 2 2 + ( − 1 ) 2 + ( − 2 ) 2 = 2 d=\\frac{|2 \\times 1-1 \\times 3-2 \\times 2-1|}{\\sqrt{2^{2}+(-1)^{2}+(-2)^{2}}}=2 d=22+(−1)2+(−2)2以上是关于代数47 ----点到平面及直线的距离的主要内容，如果未能解决你的问题，请参考以下文章

求notepad++正则表达式

无法找到 file：///F:3dmax/html/welcome.scome/index.html.请确保路径或internet

intel corporatation 82915G/GV/GL/P/PL/GL Grantsdale host bridge/DRAM Control

linux下，安装snort，输入 ./configure --prefix=/usr/local/snort --enable-mysql=/usr/

java.lang.NoClassDefFoundError: org/apache/hive/hcatalog/mapreduce/HCatOutputFor

NoClassDefFoundError: ch/qos/logback/classic/spi/ThrowableProxy