代数49---- 曲线的方程
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了代数49---- 曲线的方程相关的知识,希望对你有一定的参考价值。
形形色色的空间曲线

回顾:直线是最简单的空间曲线
直线可以看作是做匀速直线运动的质点的几何轨迹 .
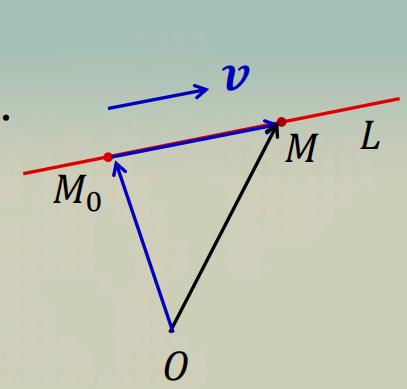
参数方程
L
{
x
=
x
0
+
m
t
y
=
y
0
+
n
t
z
=
z
0
+
p
t
,
−
∞
<
t
<
+
∞
.
L\\left\\{\\begin{array}{l} x=x_{0}+m t \\\\ y=y_{0}+n t \\\\ z=z_{0}+p t \\end{array}\\right. ,− \\infty < t < +\\infty .
L⎩⎨⎧x=x0+mty=y0+ntz=z0+pt,−∞<t<+∞.
其中
v
=
(
m
,
n
,
p
)
v=(m, n, p)
v=(m,n,p) 是速度,
t
t
t 是时间。
直线也可以看作是两平面的交线 .
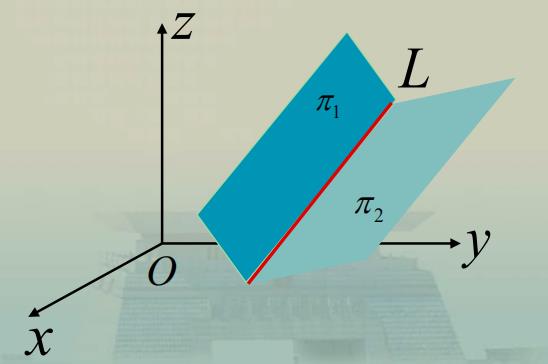
一般方程 L : { A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 \\quad L:\\left\\{\\begin{array}{l}A_{1} x+B_{1} y+C_{1} z+D_{1}=0 \\\\ A_{2} x+B_{2} y+C_{2} z+D_{2}=0\\end{array}\\right. L:{A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
空间曲线的参数方程
空间曲线可以看作是质点的运动轨迹 .
曲线
C
C
C 上动点
M
(
x
,
y
,
z
)
M(x, y, z)
M(x,y,z) 表示为
{
x
=
x
(
t
)
y
=
y
(
t
)
,
a
≤
t
≤
b
z
=
z
(
t
)
\\left\\{\\begin{array}{l} x=x(t) \\\\ y=y(t), a \\leq t \\leq b \\\\ z=z(t) \\end{array}\\right.
⎩⎨⎧x=x(t)y=y(t),a≤t≤bz=z(t)
空间曲线
C
C
C 的参数方程,
t
t
t 为参数.
【注】 空间曲线参数方程中参数可取时间、
转动角度或其它变量.
圆柱螺旋线
例
设空间一动点
M
M
M 在圆柱面
S
:
x
2
+
y
2
=
R
2
S: x^{2}+y^{2}=R^{2}
S:x2+y2=R2 上以等角速度
ω
\\omega
ω 绕
z
z
z 轴旋转, 同时又以线速度
v
v
v 沿平行
于
z
z
z 轴的正向均匀地上升.
动点
M
M
M 的轨迹称为圆柱螺旋线
.
.
.
试求圆柱螺旋线的参数方程.

{
x
=
R
cos
ω
t
y
=
R
sin
ω
t
z
=
v
t
\\begin{array}{l} \\left\\{\\begin{matrix} x=R \\cos \\omega t \\\\ y=R \\sin \\omega t \\\\ z=v t \\end{matrix}\\right. \\\\ \\end{array}
⎩⎨⎧x=Rcosωty=Rsinωtz=vt
令
θ
=
ω
t
,
b
=
v
ω
.
则
:
\\text { 令 } \\theta=\\omega t, b=\\frac{v}{\\omega} .则:
令 θ=ωt,b=ωv.则:
{
x
=
R
cos
θ
,
y
=
R
sin
θ
,
z
=
b
θ
.
\\\\ \\left\\{\\begin{matrix} x=R \\cos \\theta, \\\\ y=R \\sin \\theta, \\\\ z=b \\theta . \\end{matrix}\\right.
⎩⎨⎧x=Rcosθ,y=Rsinθ,z=bθ.
应用案例:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ed7RvUpJ-1622554842122)(…/…/…/AppData/Roaming/Typora/typora-user-images/image-20201206195552021.png)]
螺距: h = 2 π b h=2 \\pi b h=2πb
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JMqBGvih-1622554842127)(…/…/…/AppData/Roaming/Typora/typora-user-images/image-20201206195653541.png)]
空间曲线的一般方程
空间曲线可以看作是两曲面的交线 .
C
:
{
F
(
x
,
y
,
z
)
=
0
G
(
x
,
y
,
z
)
=
0
C:\\left\\{\\begin{array}{l} F(x, y, z)=0 \\\\ G(x, y, z)=0 \\end{array}\\right.
C:{F(x,y,z)=0G(x,y,z)=0
注
1
:
\\large\\color{magenta}{注1:}
注1: 空间曲线的一般方程不唯一.
可用任意两个过 C C C 的曲面 S 1 , S 2 S_{1}, S_{2} S1,S2 的方程联立的方程组来表示.
注
2
:
\\large\\color{magenta}{注2:}
注2: 空间曲线
C
C
C 位于曲面
S
1
,
S
2
S_{1}, S_{2}
S1,S2 方程的线性组合确定的曲面
Σ
\\Sigma
Σ 上:
Σ
:
λ
F
(
x
,
y
,
z
)
+
μ
G
(
x
,
y
,
z
)
=
0
,
\\Sigma: \\lambda F(x, y, z)+\\mu G(x, y, z)=0,
Σ:λF(x,y,z)+μG(x,y,z)=0, 其中
λ
,
μ
\\lambda, \\mu
λ,μ 为不全为零的实数
球面的交线
例2
方程组
{
x
2
+
y
2
+
z
2
−
2
R
z
=
0
以上是关于代数49---- 曲线的方程的主要内容,如果未能解决你的问题,请参考以下文章