《LeetCode之每日一题》：46.4的幂

Posted 2021-06-15 是七喜呀！

4的幂

• 有关题目
• • 题解

题目链接： 4的幂

有关题目

给定一个整数，写一个函数来判断它是否是 4 的幂次方。
如果是，返回 true ；否则，返回 false 。

整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4^x

示例 1：

输入：n = 16
输出：true

示例 2：

输入：n = 5
输出：false

示例 3：

输入：n = 1
输出：true

提示：

-2^31 <= n <= 2^31 - 1

题解

法一：循环
其他循环方法看2 的幂

class Solution {
public:
    bool isPowerOfFour(int n) {
        if (n < 1)
            return false;
        while(n)
        {
            if (n % 4 != 0 && n != 1)
                return false;
            else 
                n /= 4;
        }
        return true;
    }
};

时间复杂度：O(log n)
空间复杂度：O(1)

法二：二进制中1的个数

思路：①先判断是否为2的幂
//我们通过尝试发现4的幂数二进制中的1都在偶数位上
再构建mask = (10101010101010101010101010101010)，转化为16进制
mask = 0xaaaaaaaa
同过按位与运算结果为零就是4的幂，反之不成立

如何判断2 的幂

class Solution {
public:
    bool isPowerOfFour(int n) {
        return n >= 1 && (n & -n) == n && (n & 0xaaaaaaaa) == 0;//&的优先级顺序比== 要低所以我们适当加上括号
        //当然其实我们令mask = 0x2aaaaaaa就好了
        //最大4的幂数为 2^30转化为二进制我们发现在满足上面的判断条件之后只要
        //2 ^ 30 = 01000000000000000000000000000000
    }
};

时间复杂度：O(1)
空间复杂度：O(1)

法三：sqrt + lowbit

一个数 n 如果是 4 的幂，等价于 n 为	
质因数只有 2 的平方数。

因此我们可以将问题其转换：判断sqrt(n)是否为 2 的幂。

class Solution {
public:

    bool isPowerOfFour(int n) {
        if (n < 1)
            return false;
        int x = (int)sqrt(n);
        return x * x == n && (x & -x) == x; 
    }
};

//二分法实现整形sqrt()
int My_sqrt(int n)
{
    int l = 0, r = n;
    while(l < r)
    {
        long mid = l + r >> 1;
        if (mid * mid >= n)
            r = mid;
        else
            l = mid + 1;
    }
    return (int)r;
}

时间复杂度：O(log n)。log n 为二分查找所需的时间复杂度
空间复杂度：O(1)

法四：取模的性质与二项式定理

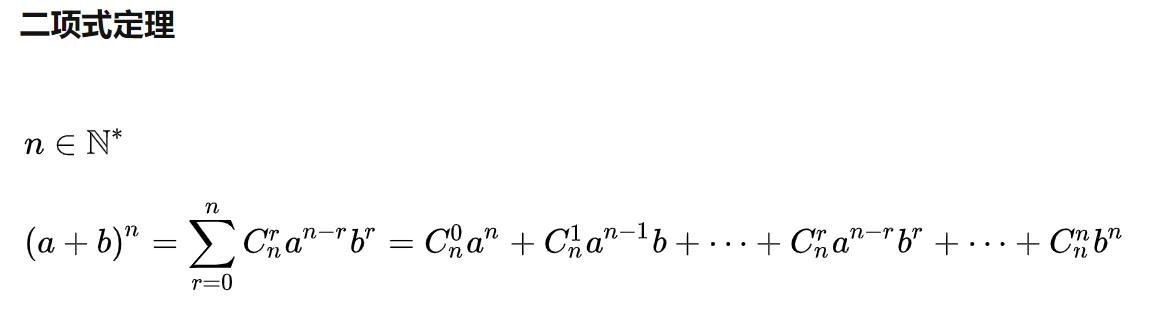
思路：通过二项式定理我们发现4的幂模3为1
2的幂模3为2
我们以此为判断条件得出答案

class Solution {
public:
    bool isPowerOfFour(int n) {
        return n >= 1 && (n & (n - 1) == 0) && n % 3 == 1;
    }
};

时间复杂度：O(1)
空间复杂度：O(1)