洛谷-----P1025 [NOIP2001 提高组] 数的划分

Posted 2021-06-15 大忽悠爱忽悠

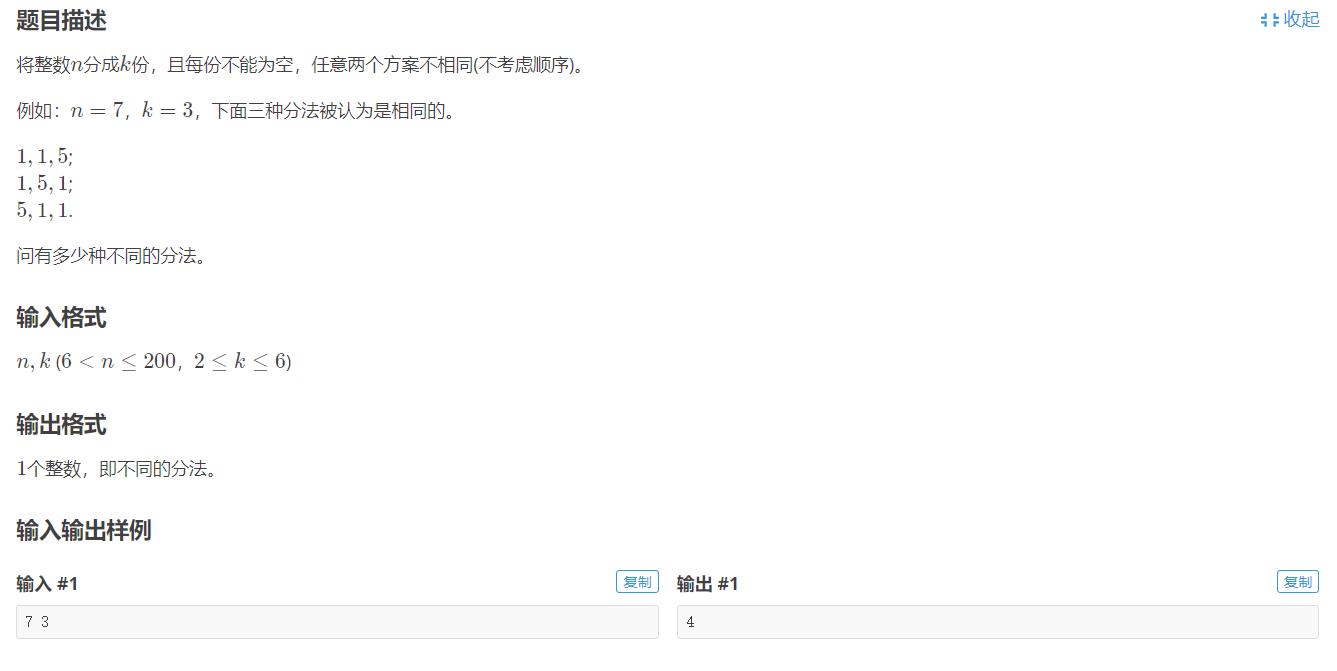
数的划分题解集合

• 回溯法思想
• 自下而上的DFS
• 动态规划---完全背包思想

---

回溯法思想

思路:

首先这里不考虑顺序，因此是组合问题

这里要求把整数n分成k份，求共有几种分法？

其实就是给你一个可选数组，数组里面元素按降序大小从1----n排列，要求你从里面选择k个数字，每一个数字可以重复选择，要求这k个数字的和等于n,问存在几种方式?

其实就是下面这道题的翻版问法:

leetcode 39. 组合总和—回溯篇2

还是把问题给树形化，变成对一个多叉树的遍历问题

下面看图:

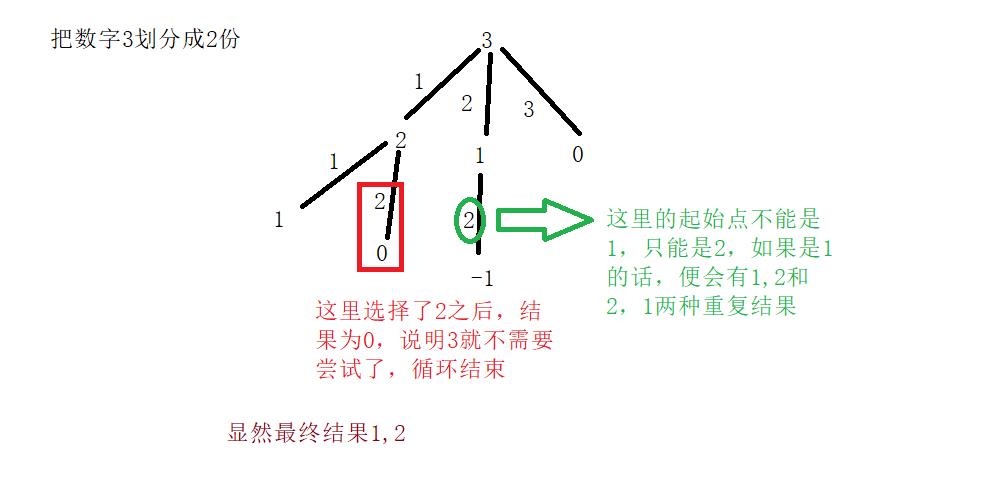
显然可以看出递归的结束条件:当前已经选择数字的个数等于k时,或者当前的需要进行划分的数字小于等于0时

这里只有等于0才算一种结果，而小于0不是符合要求的结果，并且我们其实可以把小于0的判断放入循环中，这样就不需要进行递归越界判断

这里还有一个剪枝条件:因为最开始选择的一定是最小的数字，那么如果剩余的数字全选第一个最小的数字都比当前的n要大，那么就可以结束循环了

代码:

#include<iostream>
using namespace std;
#include<vector>
class Solution
{
	int sum = 0;
public:
	int solution(int n, int k)
	{
		backTrace(n, k, 1);
		return sum;
	}
	void backTrace(int n, int k, int index)
	{
		if (k == 0)
		{
			if(n==0)
			sum++;
			return;
		}
		for (int i = index; i * k <= n; i++)
			backTrace(n - i, k - 1, i);
	}
};
int main()
{
	Solution s;
	int N = 0, K = 0;
	cin >> N >> K;
	cout << s.solution(N, K) << endl;
	return 0;
}

---

自下而上的DFS

跟上面自上而下的递归思路和减枝一样，只不过这里改成了自下而上的递归

#include<iostream>
using namespace std;
#include<vector>
int N = 0, K = 0;
class Solution
{
	int sum = 0;
public:
	int solution()
	{
		backTrace(0, 0, 1);
		return sum;
	}
	void backTrace(int n, int k, int index)
	{
		if (k ==K)
		{
			if(n==N)
			sum++;
			return;
		}
		for (int i = index; n+i*(K-k)<=N; i++)
			backTrace(n+i, k+1, i);
	}
};
int main()
{
	Solution s;
	cin >> N >> K;
	cout << s.solution() << endl;
	return 0;
}

---

动态规划—完全背包思想

与本题的动态规划思想一致：
leetcode 322. 零钱兑换----完全背包套路解法详细再探

1.dp数组含义

本题可以转化为从1-----i个物品中任意选择num个物品，每个物品数量无限，可选多次，求刚好装满背包的方案数量，背包的大小为i

那么得到dp[i][j][num]数组含义:考虑前i件物品，凑成总和j并且选择物品件数为num的方案总数

2.推导状态转移方程

注意这里物品的编号i就是物品的大小

如果不选择当前物品放入背包，那么dp[i][j][num]=dp[i-1][j][num]

如果选择当前物品放入背包，那么还需要对当前物品多次选取，累计所有可行方案数量，即

					//对每个物品考虑选择多次---当前选择物品i的总容量不能大于当前背包的容量j
					//并且当前选择的件数也不能超过限制件数k
					for (int g = 0; g * i <= j && g <= k; g++)
					{
						dp[i][j][k] += dp[i - 1][j - g * i][k - g];
					}

3.dp数组初始化

显然当我们什么物品都不考虑，并且背包容量为0的时候，为一种方案，即dp[0][0][0]=1;

代码:

#include<iostream>
using namespace std;
#include<vector>
class Solution
{
public:
	int solution(int bagSize,int num)
	{
		//这里物品的个数为bagsize  物品的最大容量也为bagsize
		vector<vector<vector<int>>> dp(bagSize+1,vector<vector<int>>(bagSize+1,vector<int>(num+1,0)));
		dp[0][0][0] = 1;
		for (int i = 1; i <= bagSize; i++)//物品维度
		{
			for (int j = 0; j <= bagSize; j++)//容量维度
			{
				for (int k = 0; k <= num; k++)//件数维度
				{
					//对每个物品考虑选择多次---当前选择物品i的总容量不能大于当前背包的容量j
					//并且当前选择的件数也不能超过限制件数k
					for (int g = 0; g * i <= j && g <= k; g++)
					{
						dp[i][j][k] += dp[i - 1][j - g * i][k - g];
					}
				}
			}
		}
		return dp[bagSize][bagSize][num];
	}
};
int main()
{
	Solution s;
	int N = 0, K = 0;
	cin >> N >> K;
	cout << s.solution(N, K) << endl;
	return 0;
}

---