leetcode 395. 至少有 K 个重复字符的最长子串----双指针篇5，滑动窗口篇4，新人理解递归必看篇！！

Posted 2021-06-15 大忽悠爱忽悠

至少有 K 个重复字符的最长子串题解集合

• 递归---分而治之
• 滑动窗口---双指针
• 总结
• 点评

---

递归—分而治之

解题思路

本题要求的一个最长的子字符串的长度，该子字符串中每个字符出现的次数都最少为 kk。

递归要点:

重点：我们在调用递归函数的时候，把递归函数当做普通函数（黑箱）来调用，即明白该函数的输入输出是什么，而不用管此函数内部在做什么。

下面是详细讲解。

1. 递归最基本的是记住递归函数的含义（务必牢记函数定义）：本题的 longestSubstring(s, k) 函数表示的就是题意，即求一个最长的子字符串的长度，该子字符串中每个字符出现的次数都最少为 k。函数入参 s 是表示源字符串；k 是限制条件，即子字符串中每个字符最少出现的次数；函数返回结果是满足题意的最长子字符串长度。
2. 递归的终止条件（能直接写出的最简单 case）：如果字符串 s 的长度少于 k，那么一定不存在满足题意的子字符串，返回 0；
3. 调用递归（重点）：如果一个字符 c 在 s 中出现的次数少于 k 次，那么 s 中所有的包含 c 的子字符串都不能满足题意。所以，应该在 s 的所有不包含 c 的子字符串中继续寻找结果：把 s 按照 c 分割（分割后每个子串都不包含 c），得到很多子字符串 t；下一步要求 t 作为源字符串的时候，它的最长的满足题意的子字符串长度（到现在为止，我们把大问题分割为了小问题(s → t)）。此时我们发现，恰好已经定义了函数 longestSubstring(s, k) 就是来解决这个问题的！所以直接把 longestSubstring(s, k) 函数拿来用，于是形成了递归。
4. 未进入递归时的返回结果：如果 s 中的每个字符出现的次数都大于 k 次，那么 s 就是我们要求的字符串，直接返回该字符串的长度。

总之，通过上面的分析，我们看出了：我们不是为了递归而递归。而是因为我们把大问题拆解成了小问题，恰好有函数可以解决小问题，所以直接用这个函数。由于这个函数正好是本身，所以我们把此现象叫做递归。小问题是原因，递归是结果。而递归函数到底怎么一层层展开与终止的，不要用大脑去想，这是计算机干的事。我们只用把递归函数当做一个能解决问题的黑箱就够了，把更多的注意力放在拆解子问题、递归终止条件、递归函数的正确性上来。

代码:

class Solution {
public:
	int longestSubstring(string s, int k) 
	{
		//递归结束条件:
		if (s.size() < k) return 0;
	   //通过一个哈希表统计当前字符串s中每个字符出现的次数
		unordered_map<int, int> counter;
		for (char c : s)//范围for
			counter[c]++;
		//用一个set容器保存s中出现过的所有字符，这样可以去除掉重复字符
		unordered_set<int> chars(s.begin(), s.end());
		//对chars容器中的不重复字符进行遍历，看是否每个字符的出现次数都大于k
		for (char c : chars)//范围for语句
		{
			//用来保存当前s中不包含当前字符c的所有子串
			vector<string> t;
			//当前字符的出现次数小于k，不满足条件，我们需要对当前s中不包含当前字符的子串进行再判断
			if (counter[c] < k)
			{
				//下面我们需要通过一个函数split，完成将不包含当前字符c的所有子串放入容器t中
				split(s, t, c);
				//用res来保存当前字符串中满足条件的最长长度
				int res = 0;
				for (string n : t)
				{
					res = max(res, longestSubstring(n, k));
				}
				return res;
			}
		}
		//如果当前字符串中每个字符的出现次数都满足大于k，那么返回当前字符串长度
		return s.size();
 	}
	void split(const string& s, vector<string>& sv, const char flag = ' ')
	{
		//清空sv容器，防止上一次保存的子串掺入到当前运算中
		sv.clear();
		//因为我们一会要用getline读取数据，而getline函数的定义如下:
		//istream& getline (istream&  is, string& str, char delim);
		//istream& getline (istream&  is, string& str);
		//而这里我们第一个参数按理应该填入字符串s，但string流不是istream流，因此要进行转换，通过istringstream
		istringstream iss(s);
		//每一次将当前分割的字符放入temp字符串中
		string temp;
		//每次遇到分割结束符flag，结束当前读取一次
		while (getline(iss, temp, flag))
		{
			sv.push_back(temp);
		}
	}
};

---

滑动窗口—双指针

思路:

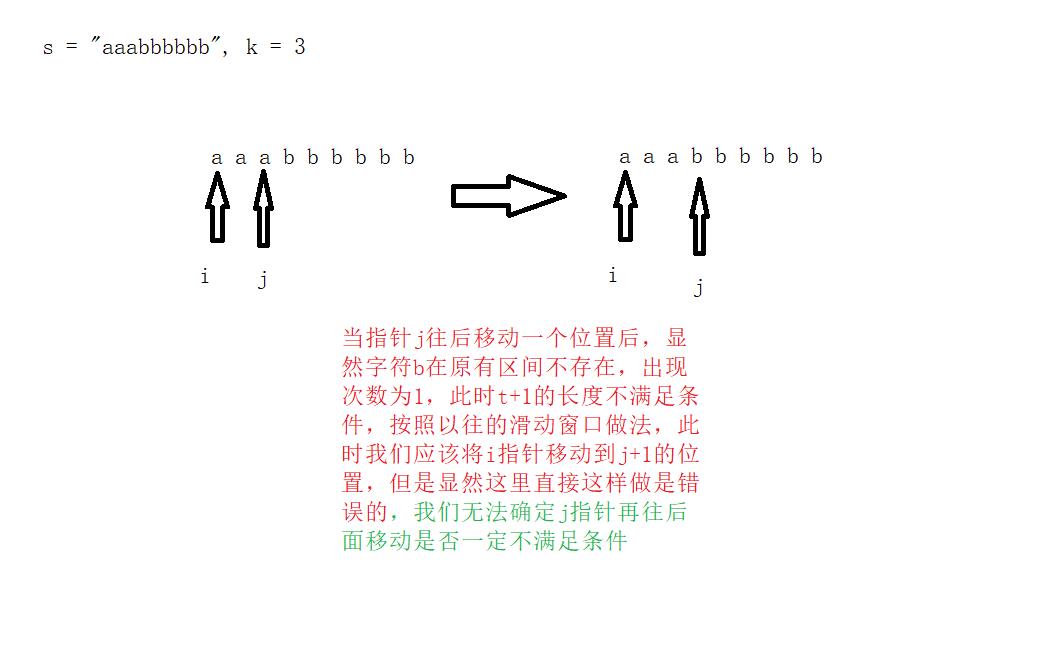
假设有长度 t 的一段区间满足要求的话，t + 1 长度的区间是否「一定满足」或者「一定不满足」呢？

显然并不一定，是否满足取决于 t + 1 个位置出现的字符在不在原有区间内。

举个🌰吧，假设我们已经画出来一段长度为 t 的区间满足要求（且此时 k > 1），那么当我们将长度扩成 t + 1 的时候（无论是往左扩还是往右扩）：

• 如果新位置的字符在原有区间出现过，那必然还是满足出现次数大于 k，这时候 t + 1 的长度满足要求

• 如果新位置的字符在原有区间没出现过，那新字符的出现次数只有一次，这时候 t + 1 的长度不满足要求

因此我们无法是使用「二分」，相应的也无法直接使用「滑动窗口」思路的双指针。

因为双指针其实也是利用了二段性质，当一个指针确定在某个位置，另外一个指针能够落在某个明确的分割点，使得左半部分满足，右半部分不满足。

图解:

那么还有什么性质可以利用呢？这时候要留意数据范围「数值小」的内容。

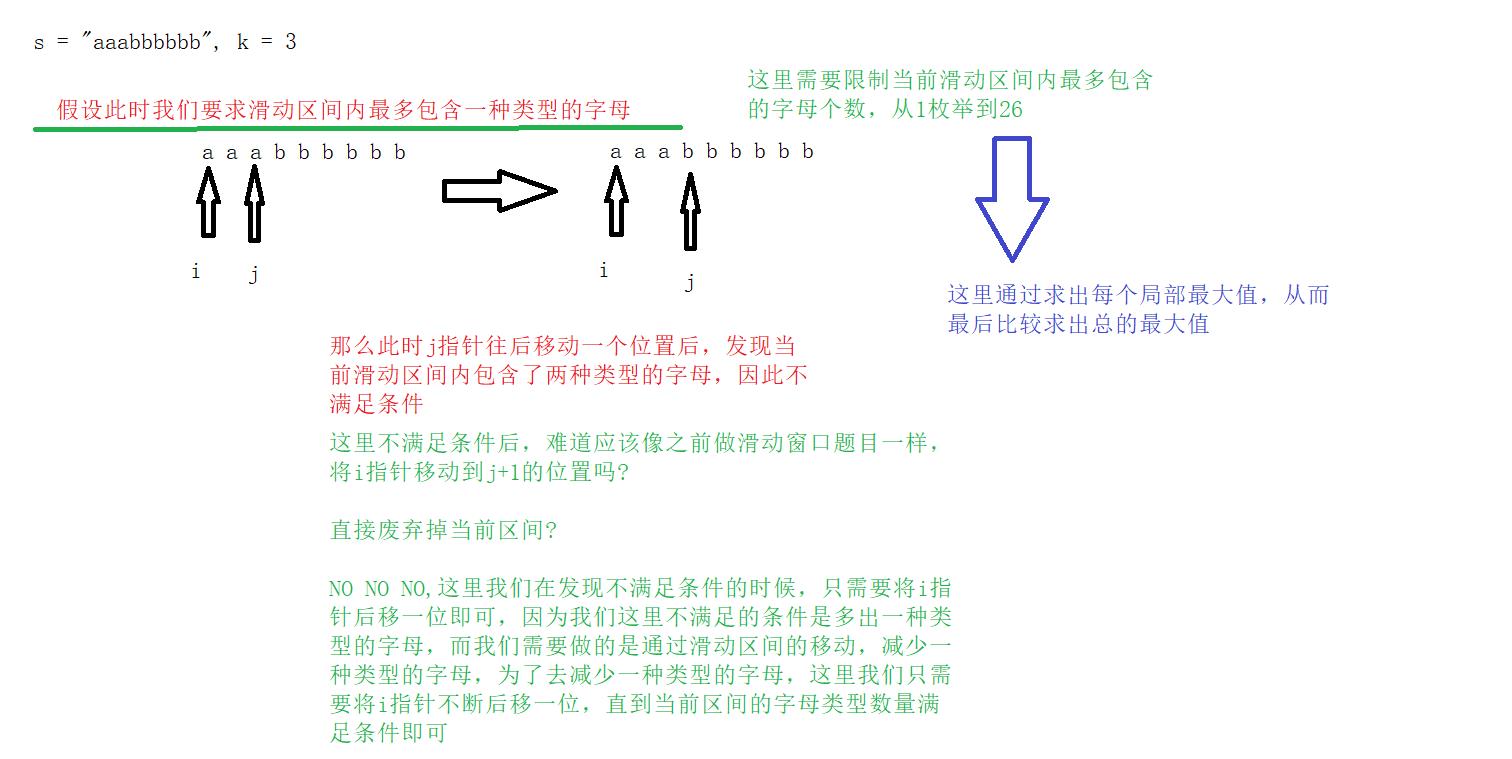
题目说明了只包含小写字母（26 个，为有限数据），我们可以枚举最大长度所包含的字符类型数量，答案必然是 [1, 26]，即最少包含 1 个字母，最多包含 26 个字母。

你会发现，当确定了长度所包含的字符种类数量时，区间重新具有了二段性质。

当我们使用双指针的时候：

• 右端点往右移动必然会导致字符类型数量增加（或不变）
• 左端点往右移动必然会导致字符类型数量减少（或不变）

当然，我们还需要记录有多少字符符合要求（出现次数不少于 k），当区间内所有字符都符合时更新答案。

图解:

代码:

class Solution {
public:
	int longestSubstring(string s, int k) 
	{
		int n = s.length();
		int ans = 0;
		int cnt[26];
		//字母限制个数从1开始枚举到26
		for (int p = 1; p<=26; p++)
		{
			//当我们重新计算局部最优解时，需要更新arr数组的值
			fill(cnt, cnt + 26, 0);
			//tot:当前[i,j]区间内的字符类型数量  
			//sum:满足出现次数大于k的字符种类个数
			for (int i = 0, j = 0, tot = 0, sum = 0; j < n; j++)
			{
				//获取当前j指针指向的字符
				int u = s[j] - 'a';
				//对应的当前字符的出现次数加一
				cnt[u]++;
				//如果添加到 cnt 之后为 1，说明字符总数 +1
				if (cnt[u] == 1)  tot++;
				// 如果添加到 cnt 之后等于 k，说明该字符从不达标变为达标，达标数量 + 1
				if (cnt[u] == k) sum++;
				// 当区间所包含的字符种类数量 tot 超过了当前限定的数量 p，
				//那么我们要删除掉一些字母，即「左指针」右移
				while (tot > p)
				{
					//左指针右移一位，然后将原来左指针指向的字符的出现个数减去1
					int t = s[i++] - 'a';
					cnt[t]--;
					// 如果添加到 cnt 之后为 0，说明字符总数-1
					if (cnt[t] == 0)  tot--;
					// 如果添加到 cnt 之后等于 k - 1，说明该字符从达标变为不达标，达标数量 - 1
					if (cnt[t] == k - 1) sum--;
				}
				// 当所有字符都符合要求，更新当前局部最优解的答案
				//tot是当前滑动区间内包含的字符类型总数
				//sum满足出现次数大于k的字符种类个数
				//当两者相等时，说明当前滑动区间内的字符都满足条件，此时才需要对ans进行更新
				if(tot==sum)
				ans = max(ans, j - i + 1);
			}
		}
		return ans;
 	}
};

---

总结

「当确定了窗口内所包含的字符数量时，区间重新具有了二段性质」。这是本题的滑动窗口解法和迄今为止做的滑动窗口题目的最大不同，本题需要手动增加限制，即限制窗口内字符种类。

【补充】这里解释一下「为什么需要先枚举 26 种可能性」：

首先我们知道「答案子串的左边界左侧的字符以及右边界右侧的字符一定不会出现在子串中，否则就不会是最优解」。

但如果我们只从该性质出发的话，朴素解法应该是使用一个滑动窗口，不断的调整滑动窗口的左右边界，使其满足「左边界左侧的字符以及右边界右侧的字符一定不会出现在窗口中」，这实际上就是双指针解法，但是如果不先敲定（枚举）出答案所包含的字符数量的话，这里的双指针是不具有单调性的。

换句话说，只利用这一性质是没法完成逻辑的。

这时候我们面临的问题是：性质是正确的，但是还无法直接利用。

因此我们需要先利用字符数量有限性（可枚举）作为切入点，使得「答案子串的左边界左侧的字符以及右边界右侧的字符一定不会出现在子串中」这一性质在双指针的实现下具有单调性。也就是题解说的「让区间重新具有二段性质」。

然后遍历 26 种可能性（答案所包含的字符种类数量），对每种可能性应用滑动窗口（由上述性质确保正确），可以得到每种可能性的最大值（局部最优），由所有可能性的最大值可以得出答案（全局最优）。

---

点评

这道题的突破口分析其实和 1178. 猜字谜 类似。

解决思路：当我们采用常规的分析思路发现无法进行时，要去关注一下数据范围中「数值小」的值。因为数值小其实是代表了「可枚举」，往往是解题或者降低复杂度的一个重要（甚至是唯一）的突破口。