3.1循环神经网络数学理解
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了3.1循环神经网络数学理解相关的知识,希望对你有一定的参考价值。
文章目录
在前馈神经网络中,信息的传递是单向的,这种限制虽然使得网络变得更容易学习,但在一定程度上也减弱了神经网络模型的能力。在生物神经网络中,神经元之间的连接关系要复杂的多。 前馈神经网络可以看作是一个复杂的函数,每次输入都是独立的,即网络的输出只依赖于当前的输入。但是在很多现实任务中,网络的输入不仅和当前时刻的输入相关,也和其过去一段时间的输出相关。因此,前馈网络难以处理时序数据,比如视频、语音、文本等。时序数据的长度一般是不固定的,而前馈神经网络要求输入和输出的维数都是固定的,不能任意改变。因此,当处理这一类和时序相关的问题时,就需要一种能力更强的模型。
循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络。在循环神经网络中,神经元不但可以接受其它神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。和前馈神经网络相比,循环神经网络更加符合生物神经网络的结构。循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。循环神经网络的参数学习可以通过随时间反向传播算法来学习。
1、给网络增加记忆能力
为了处理这些时序数据并利用其历史信息,我们需要让网络具有短期记忆能力。而前馈网络是一个静态网络,不具备这种记忆能力。
1.1、延时神经网络
一种简单的利用历史信息的方法是建立一个额外的延时单元,用来存储网络的历史信息(可以包括输入、输出、隐状态等)。比较有代表性的模型是延时神经网络。
延时神经网络是在前馈网络中的非输出层都添加一个延时器,记录最近几次神经元的输出。在第
t
t
t 个时刻,第
l
+
1
l+1
l+1 层神经元和第
l
l
l 层神经元的最近
p
p
p 次输出相关,即:
h
t
(
l
+
1
)
=
f
(
h
t
(
l
)
,
h
t
−
1
(
l
)
,
.
.
.
,
h
t
−
p
(
l
)
)
h_t^{(l+1)}=f(h_t^{(l)},h_{t-1}^{(l)},...,h_{t-p}^{(l)})
ht(l+1)=f(ht(l),ht−1(l),...,ht−p(l))
延时神经网络在时间维度上共享权值,以降低参数数量。因此对于序列输入来讲,延时神经网络就相当于卷积神经网络。
1.2、有外部输入的非线性自回归模型
**自回归模型(Autoregressive Model,AR)**是统计学上常用的一类时间序列模型,用一个变量
y
t
y_t
yt的历史信息来预测自己:
y
t
=
w
0
+
∑
i
=
1
p
w
p
y
t
−
i
+
ϵ
t
y_t=w_0+\\sum_{i=1}^{p}{w_py_{t-i}}+\\epsilon_t
yt=w0+i=1∑pwpyt−i+ϵt
其中
p
p
p为超参数,
w
p
w_p
wp为参数,
ϵ
t
∼
N
(
0
,
σ
2
)
\\epsilon_t\\sim N(0,\\sigma^2)
ϵt∼N(0,σ2)为第t个时刻的噪声,方差
σ
2
\\sigma^2
σ2和时间无关。
有外部输入的非线性自回归模型(Nonlinear Autoregressive with Exogenous Inputs Model,NARX)是自回归模型的扩展,在每个时刻
t
t
t都有一个外部输入
x
t
x_t
xt ,产生一个输出
y
t
y_t
yt 。NARX通过一个延时器记录最近几次的外部输入和输出,第
t
t
t个时刻的输出
y
t
y_t
yt 为:
y
t
=
f
(
x
t
,
x
t
−
1
,
.
.
.
,
x
t
−
p
,
y
t
−
1
,
y
t
−
2
,
.
.
.
,
y
t
−
q
)
y_t=f(x_t,x_{t-1},...,x_{t-p},y_{t-1},y_{t-2},...,y_{t-q})
yt=f(xt,xt−1,...,xt−p,yt−1,yt−2,...,yt−q)
其中
f
(
⋅
)
f(·)
f(⋅) 表示非线性函数,可以是一个前馈网络,
p
p
p和
q
q
q为超参数。
2. 基本循环神经网络
循环神经网络在隐藏层会对之前的信息进行存储记忆,然后输入到当前计算的隐藏单元中,也就是隐藏层的内部节点不再是相互独立的,而是互相有消息传递。隐藏层的输入不仅可以由两部分组成,输入层的输出和隐藏层上一时刻的输出,即隐藏层内的节点自连;隐藏层的输入还可以由三部分组成,输入层的输出、隐藏层上一时刻的输出、上一隐藏层的状态,即隐藏层内的节点不仅自连还互连。结构如图1所示。
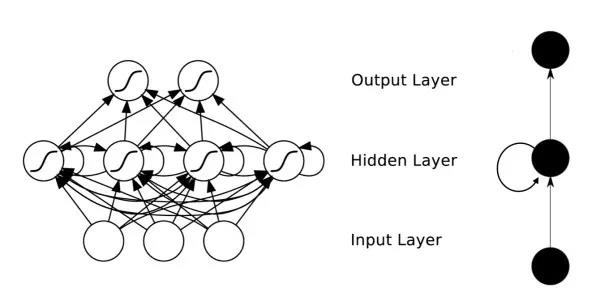
图 1 : 循 环 神 经 网 络 结 构 图 图1:循环神经网络结构图 图1:循环神经网络结构图
如果我们把上图右边部分展开,循环神经网络也可以画成下面这个样子:
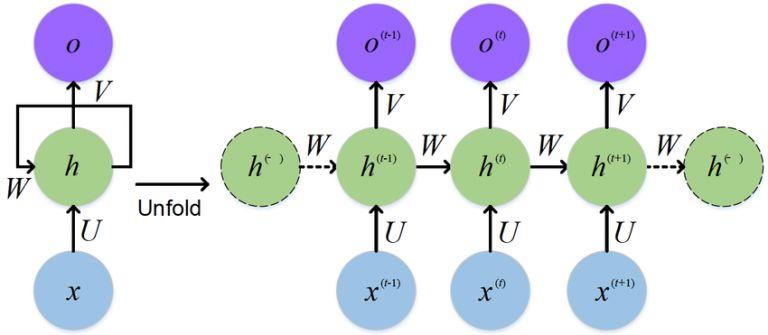
图 2 : 循 环 神 经 网 络 展 开 图 图2:循环神经网络展开图 图2:循环神经网络展开图
对于图2的网络,计算过程如下:
-
x t x^t xt表示第 t t t步(step)的输入。比如 x 1 x^1 x1为第二个词的词向量( x 0 x^0 x0为第一个词);
-
h t h^t ht为隐藏层的第 t t t步的状态,它是网络的记忆单元。 h t h^t ht根据当前输入层的输出与上一时刻隐藏层的状态 h t − 1 h^{t-1} ht−1 进行计算,如公式1所示。其中, U U U是输入层到隐藏层的权重矩阵,权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重, b b b为偏置。 f ( x ) f(x) f(x)一般是非线性的激活函数,如 t a n h tanh tanh或 R e L U ReLU ReLU。
h t = f ( U x t + W h t − 1 + b ) (1) h_t=f(Ux^{t}+Wh^{t-1}+b)\\tag{1} ht=f(Uxt+Wht−1+b)(1) -
o t o^t ot是第 t t t步的输出。输出层是全连接层,即它的每个节点和隐含层的每个节点都互相连接,V是隐藏层到输出层的权重矩阵, g ( x ) g(x) g(x)是激活函数。
o t = g ( V ∗ h t ) (2) o^t=g(V*h^t)\\tag{2} ot=g(V∗ht)(2)
如果将(1)式循环带入(2)式可得:
KaTeX parse error: No such environment: equation at position 8: \\begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \\begin{split}…
由式(3)可以看出,循环神经网络的输出值与前面多个时刻的历史输入值有关,这就是为何循环神经网络能够往前看任意多个输入值的原因,也就是为何循环神经网络能够对序列数据建模的原因。
3. 双向循环神经网络
3.1 双向循环神经网络的介绍
对于语言模型来说,很多时候单向循环神经网络表现是不好的,比如下面这句话:
我的手机坏了,我打算____一部新手机。
可以想象,如果我们只看横线前面的词,手机坏了,那么我是打算修一修?换一部新的?还是大哭一场?这些都是无法确定的。但如果我们也看到了横线后面的词是『一部新手机』,那么,横线上的词填『买』的概率就大得多了。
对于上面的语言模型,单向循环神经网络是无法对此进行建模的。因此,我们需要用双向循环神经网络,如图3所示。
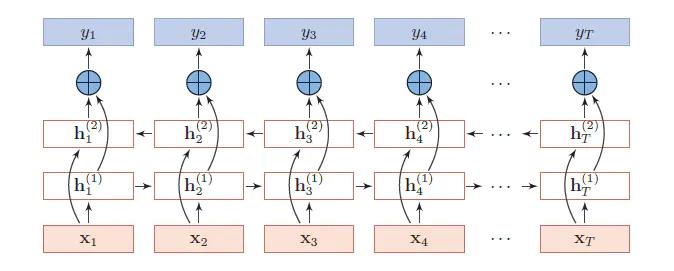
图
3
:
双
向
循
环
神
经
网
络
以上是关于3.1循环神经网络数学理解的主要内容,如果未能解决你的问题,请参考以下文章