UVA10589 Area计算几何

Posted 2021-06-14 海岛Blog

Measuring the area of a certain shape is an important part of certain geometric problems. When the shape becomes complex it often becomes very difficult to measure the area of that geometric shape. In some of these cases some randomized algorithms helps us immensely to find the area roughly. In this problem we will find such an area with randomized algorithm.
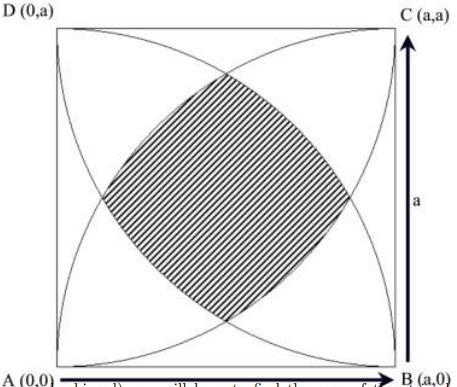
    Look at the picture on the right. ABCD is a square whose sides are a. A circle is drawn (1/4 th of a circle I should say) considering A as its center. Its radius is a. Three similar circles are drawn considering B, C, D as centers. Using an algorithm based on random numbers (The random number generator may be biased) you will have to find the area of the striped region.
    The idea is that you will be given N pairs of random coordinates within the rectangle. If M of them are within the striped region then the approximate area of the striped region A = M ∗ a ∗ a/N. You are to find the approximate area using this concept.

Input
The input file contains several sets of inputs. The description of each set is given below.
    The first line of each set contains two integers N (N can always be written in the form 10^k where k is a non-negative integer less than 6), a (100 > a ≥ 10). Each of the next N lines contains two floatingpoint numbers, which indicates the coordinate of a point. These floating-point numbers always have seven digits after the decimal point and the coordinates are always within the rectangle. Points just on the boundaries of the striped region are considered within the striped region. Points just outside are considered out of the striped region and vice versa. Assume that the lower left corner of the rectangle is (0, 0) and top right corner is (a, a) as shown in the figure above.
    Input is terminated by a set whose N is zero.
Output
For each of input you should produce one line of output. This line should contain the area of the striped region according to the formula specified above. Your answer must be exact and no floating-point errors will be tolerated. That means precision of calculation must be infinite or precision error must be zero. Output numbers should always have five digits after the decimal point.
Sample Input
1 10
5.0000000 5.0000000
0 0
Sample Output
100.00000

问题链接：UVA10589 Area
问题简述：计算上图阴影部分面积。
问题分析：计算几何问题，不解释。
程序说明：（略）
参考链接：（略）
题记：（略）

AC的C++语言程序如下：

/* UVA10589 Area */

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int n, a;
    while (~scanf("%d%d", &n, &a) && (n || a)) {
        int cnt = 0;
        double x, y;
        for (int i = 1; i <= n; i++) {
            scanf("%lf%lf", &x, &y);
            if (x * x + y * y <= a * a &&
                    (x - a) * (x - a) + y * y <= a * a &&
                    x * x + (y - a) * (y - a) <= a * a &&
                    (x - a) * (x - a) + (y - a) * (y - a) <= a * a)
                cnt++;
        }

        printf("%.5lf\\n", (double)cnt * a * a / n);
    }

    return 0;
}