Dijkstra C++ 邻接矩阵

Posted 2023-04-01

求可以调试通过的正确代码！！！谢谢！！！！

自己写的，你可你把里面的主体提出来单做一个函数，测试通过。

#include <stdio.h>
#include <string.h>
#define MAX 20
int mincost(int V[], int D[], int n);
int main()

int C[MAX][MAX]; //邻接矩阵
int D[MAX], V[MAX] = 0 ; /*数组V用来表示每次计算加入集合V的点，1为加入了，0为还没有加入*/
int n, i, j, k, w, sum;
printf("请输入顶点个数:");
scanf("%d", &n);
printf("\n请输入建立后的临接矩阵(用n*n矩阵表示), 输入100000表示无穷大:\n");
for(i = 1; i <= n; i++)

for(j = 1; j <= n; j++)

scanf("%d", &C[i][j]);


//以下部分可以提出作为一个函数，计算最短路
V[1] = 1; /*1为源点*/
for(i = 1; i <= n; i++)

D[i] = C[1][i]; /*D置初值*/

for(i = 1; i <= n; i++)

/*从集合S(即没有经过计算的点）中选出一个点w（即V中值为0），使D[w]值最小*/
w = mincost(V, D, n);
V[w] = 1;
/*由于w的选定，S中的每个点(即V中值为0的点都要重新计算其到源点的最小值*/
for(k = 2; k <= n; k++)

if(V[k] == 0)

sum = D[w] + C[w][k];
if(sum < D[k])

D[k] = sum;




for(i = 2; i <= n; i++)

printf("D[%d] = %d\n", i, D[i]);

memset(V, 0, MAX * sizeof(int)); /*初始化*/
return 0;


int mincost(int V[], int D[], int n)

int temp = 10000000, i, w = 2;
for(i = 2;i <= n; i++)

if(V[i] == 0 && D[i] < temp)

temp = D[i];
w = i;


return w;
参考技术A 网上一找就能找到

基于邻接矩阵的Dijkstra算法——C++实现

一、前言

本文实现的Dijkstra(迪杰斯特拉)算法包含如下功能：

• 可指定起始点和初始点
• 能够计算起始点和初始点之间的最短路径长度
• 能够输出起始点和初始点之间的最短路径(中间节点)

本文中我们使用到的图如下：

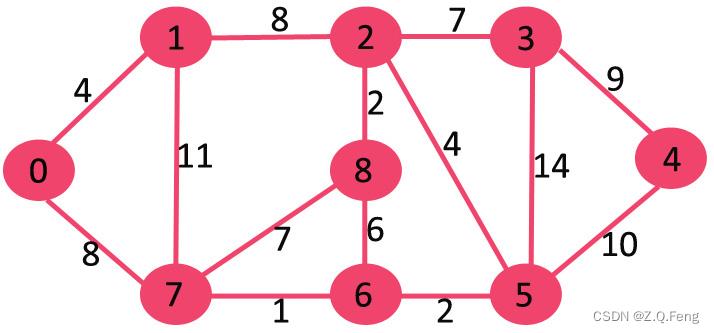
运行效果如下(代码中节点从 1 开始，其对应上图中路径为0-1-2-8)：

---

二、数据准备

将上图中一共有9个顶点、14条边，对应的是一个9x9的邻接矩阵，储存这些数据到edges.txt文件中：

9 14
0 4 0 0 0 0 0 8 0
4 0 8 0 0 0 0 11 0
0 8 0 7 0 4 0 0 2
0 0 7 0 9 14 0 0 0
0 0 0 9 0 10 0 0 0
0 0 4 0 10 0 2 0 0
0 0 0 14 0 2 0 1 6
8 11 0 0 0 0 1 0 7
0 0 2 0 0 0 6 7 0

邻接矩阵中的值为对应路径之间的权值(可为浮点数，但是必须以空格分隔)，不相连的点之间我们记权值为 0。

---

三、头文件及数据结构

定义结构体MGraph储存图的所有信息：

#include<climits>
#include<iostream>
#include <fstream>
using namespace std;

#define MaxSize 100

typedef double MAT[MaxSize][MaxSize];

//图的邻接矩阵存储结构
typedef struct
    //邻接矩阵
    MAT edges;
    //图中当前的顶点数和边数
    int vexnum, arcnum;
MGraph;

---

四、Dijkstra算法

代码如下：

// Function to print shortest path from source to j
// using parent array(not include the begin node)
void printPath(int parent[], int j)
    // Base Case : If j is source
    if (parent[j] == -1)
        return;
    printPath(parent, parent[j]);
    cout << j << " ";


// this method returns a minimum distance for the
// vertex which is not included in Tset.
int minimumDist(double dist[], bool Tset[], int count)
    int i, min = INT_MAX, index;
    for(i = 1; i <= count; i++)
        if(Tset[i]==false && dist[i]<=min)
            min = dist[i];
            index = i;
        
    
    return index;


double Dijkstra(MGraph *G, int src, int end, int flag)
	/*
	Reference :
		https://www.educative.io/edpresso/how-to-implement-dijkstras-algorithm-in-cpp
	modified by z.q.feng at 2022.05.29
	*/
    int i, j, m;
    // integer array to calculate minimum distance for each node.
    double dist[MaxSize];
    // boolean array to mark visted/unvisted for each node.
    bool Tset[MaxSize];
    // Parent array to store shortest path tree
	int parent[MaxSize];

    // set the nodes with infinity distance except for the
    // initial node and mark them unvisited.
    for(i = 1; i <= G->vexnum; i++)
        dist[i] = INT_MAX;
        Tset[i] = false;
        parent[i] = -1;
    
    // Source vertex distance is set to zero.
    dist[src] = 0;

    for(i = 1; i <= G->vexnum; i++)
        // vertex not yet included.
        m = minimumDist(dist, Tset, G->vexnum);
        // m with minimum distance included in Tset.
        Tset[m] = true;
        for(j = 1; j <= G->vexnum; j++)
            // Updating the minimum distance for the particular node.
            if(!Tset[j] && G->edges[m][j] && dist[m] != INT_MAX
                && dist[m] + G->edges[m][j] < dist[j])
                parent[j] = m;
                dist[j] = dist[m] + G->edges[m][j];
            
        
    
    // 设置flag值为1以输出该条最短路径
    if (flag)
        cout << src << " ";
    	printPath(parent, end);
        cout << endl;
    
    return dist[end];

---

五、运行示例

编写主函数如下，读取edges.txt文件中的数据并查看节点 1 和 9 之间的最短路径及其长度：

int main(int argc, char const *argv[])

	int i, j;
	MGraph G;
	// 从文件中读取数据
    ifstream fin;
    fin.open("edges.txt");
    // 顶点数 边数
    fin >> G.vexnum >> G.arcnum;
    // 读取带权邻接矩阵(空格分割)
    for (i = 1; i <= G.vexnum; i++)
        for (j = 1; j <= G.vexnum; j++)
            fin >> G.edges[i][j];
    fin.close();
    int src = 1, end = 5, m;
    cout<<"\\n\\tThe shortest path from "<<src<<" to "<<end<<" is\\n\\n\\t\\t";
    // 设置flag值为1以打印该条路径
    m = Dijkstra(&G, src, end, 1);
    cout<<"\\n\\tThe shortest distance is "<<m<<endl;
	return 0;

输出如下所示，注：代码中的节点均从 1 开始，若图中初始节点为 0，需要做对应修改：

代码中节点从 1 开始，其对应上图中路径为0-7-6-5-4。

---

六、总结

无