一文学懂经典算法系列之：直接选择排序

Posted 2021-06-14 一头小山猪

写在前面：博主是一只经过实战开发历练后投身培训事业的“小山猪”，昵称取自动画片《狮子王》中的“彭彭”，总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域，如今终有小成，愿将昔日所获与大家交流一二，希望对学习路上的你有所助益。同时，博主也想通过此次尝试打造一个完善的技术图书馆，任何与文章技术点有关的异常、错误、注意事项均会在末尾列出，欢迎大家通过各种方式提供素材。

• 对于文章中出现的任何错误请大家批评指出，一定及时修改。
• 有任何想要讨论和学习的问题可联系我：[e-mail]。
• 发布文章的风格因专栏而异，均自成体系，不足之处请大家指正。

一文学懂经典算法系列之：直接选择排序

本文关键字：经典算法、排序算法、选择排序、直接选择排序、算法实践

文章目录

• 一文学懂经典算法系列之：直接选择排序
• • 一、什么是算法
  • • 1. 算法的定义
    • 2. 补充的概念
  • 二、选择排序
  • • 1. 选择排序介绍
    • 2. 直接选择排序
    • 3. 伪代码
  • 三、算法实践
  • • 1. 算法实现
    • 2. 时间复杂度
    • 3. 空间复杂度

一、什么是算法

本专栏为《手撕算法》栏目的子专栏：《经典算法》，会讲述一些经典算法，并进行分析。在此之前我们要先了解什么是算法，能够解决什么样的问题。

1. 算法的定义

以下为经典教材《Introduction.to.Algorithms》开篇中的内容。

Informally, an algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. An algorithm is thus a sequence of computational steps that transform the input into the output.

可以看到，任何被明确定义的计算过程都可以称作算法，它将某个值或一组值作为输入，并产生某个值或一组值作为输出。所以算法可以被称作将输入转为输出的一系列的计算步骤。
这样的概括是比较标准和抽象的，其实说白了就是步骤明确的解决问题的方法。由于是在计算机中执行，所以通常先用伪代码来表示，清晰的表达出思路和步骤，这样在真正执行的时候，就可以使用不同的语言来实现出相同的效果。
概括的说，算法就是解决问题的工具。在描述一个算法时，我们关注的是输入与输出。也就是说只要把原始数据和结果数据描述清楚了，那么算法所做的事情也就清楚了。我们在设计一个算法时也是需要先明确我们有什么和我们要什么，这一点相信大家在后面的文章中会慢慢体会到。

2. 补充的概念

• 数据结构

算法经常会和数据结构一起出现，这是因为对于同一个问题（如：排序），使用不同的数据结构来存储数据，对应的算法可能千差万别。所以在整个学习过程中，也会涉及到各种数据结构的使用。
常见的数据结构包括：数组、堆、栈、队列、链表、树等等。

• 算法的效率

在一个算法设计完成后，还需要对算法的执行情况做一个评估。一个好的算法，可以大幅度的节省运行的资源消耗和时间。在进行评估时不需要太具体，毕竟数据量是不确定的，通常是以数据量为基准来确定一个量级，通常会使用到时间复杂度和空间复杂度这两个概念。

• 时间复杂度

通常把算法中的基本操作重复执行的频度称为算法的时间复杂度。算法中的基本操作一般是指算法中最深层循环内的语句（赋值、判断、四则运算等基础操作）。我们可以把时间频度记为T(n)，它与算法中语句的执行次数成正比。其中的n被称为问题的规模，大多数情况下为输入的数据量。
对于每一段代码，都可以转化为常数或与n相关的函数表达式，记做f(n)。如果我们把每一段代码的花费的时间加起来就能够得到一个刻画时间复杂度的表达式，在合并后保留量级最大的部分即可确定时间复杂度，记做O(f(n))，其中的O就是代表数量级。
常见的时间复杂度有（由低到高）：O(1)、O(${\log }_{2}n$)、O(n)、O($n{\log }_{2}n$)、O($n^2$)、O($n^3$)、O($2^n$)、O(n!)。

• 空间复杂度

程序从开始执行到结束所需要的内存容量，也就是整个过程中最大需要占用多少的空间。为了评估算法本身，输入数据所占用的空间不会考虑，通常更关注算法运行时需要额外定义多少临时变量或多少存储结构。如：如果需要借助一个临时变量来进行两个元素的交换，则空间复杂度为O(1)。

• 伪代码约定

伪代码是用来描述算法执行的步骤，不会具体到某一种语言，为了表达清晰和标准化，会有一些约定的含义：
缩进：表示块结构，如循环结构或选择结构，使用缩进来表示这一部分都在该结构中。
循环计数器：对于循环结构，在循环终止时，计数器的值应该为第一个超出界限的值。
to：表示循环计数器的值增加。
downto：表示循环计数器的值减少。
by：循环计数器的值默认变化量为1，当大于1时可以使用by。
变量默认是局部定义的。
数组元素访问：通过"数组名[下标]"形式，在伪代码中，下标从1开始（"A[1]“代表数组A的第一个元素）。
子数组：使用”…"来代表数组中的一个范围，如"A[i…j]"代表从第i个到第j个元素组成的子数组。
对象与属性：复合的数据会被组织成对象，如链表包含后继（next）和存储的数据（data）,使用“对象名 + 点 + 属性名”。
特殊值NIL：表示指针不指向任何对象，如二叉树节点无子孩子可认为左右子节点信息为NIL。
return：返回到调用过程的调用点，在伪代码中允许返回多个值。
and和or：与运算和或运算默认短路，即如果已经能够确定表达式结果时，其他条件不会去判断或执行。

二、选择排序

1. 选择排序介绍

选择排序的核心思想是：每一趟从无序区中选出关键字最小的元素，按顺序放在有序区的最后（生成新的有序区，无序区元素个数减1），直到全部排完为止。

• 直接选择排序

也称简单选择排序，整个过程就是每一趟都将无序区中的所有元素进行逐一比较，找到最小的元素，与无序区中的首个元素进行交换，有序区长度加1，无序区长度减1。重复以上步骤，直到所有的元素均已排好。

• 树形选择排序

也称锦标赛排序，是为了优化每次在无序区中确定最小元素时比较次数过多的问题。核心思想是借助树形结构对整个序列进行两两比较，将数值较小的元素作为优胜者上升到父节点。最后能够在树形结构中记录每一次优胜者之间的关系，按规则取出即可。

• 堆排序

堆排序是对树形选择排序的优化，由于树形选择排序需要花费较多的存储空间，堆排序的主要思想是构建一个小顶堆（升序排列中）。整个的过程就是不断的弹出堆顶元素，归入有序区，然后继续将堆中剩余元素调整为小顶堆，重复这个过程，直到排好所有元素。

2. 直接选择排序

• 输入

n个数的序列，通常直接存放在数组中，可能是任何顺序。

• 输出

输入序列的一个新排列，满足从小到大的顺序（默认讨论升序，简单的修改就可以实现降序排列）。

• 算法说明

直接选择排序的主要步骤是：在第1趟中，从n个记录中找出关键字最小的记录与第1个记录交换；在第2趟中，从n-1个记录中找出关键字最小的记录与第2个记录交换；可以归纳为：在第i趟中，从n-i+1个记录中找出关键字最小的记录与第i个记录交换；直到完成i=n-1时的操作，此时整个序列有序。

• 算法流程

如果使用直接选择排序对元素个数为n的序列进行排序，需要进行n-1趟排序。

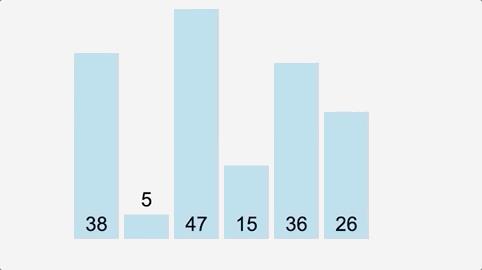
1. 第1趟：找出最小元素 5，与第1个元素38交换 -> 5，38，47，15，36，26
2. 第2趟：找出最小元素15，与第2个元素38交换 -> 5，15，47，38，36，26
3. 第3趟：找出最小元素26，与第3个元素47交换 -> 5，15，26，38，36，47
4. 第4趟：找出最小元素36，与第4个元素38交换 -> 5，15，26，36，38，47
5. 第5趟：找出最小元素38，已在对应位置无需交换 -> 5，15，26，36，38，47

3. 伪代码

for i = 1 to n - 1
    k = i
    for j = i + 1 to n
        if A[j] < A[k]
            k = j
    if k != i
        exchange A[i] with A[k]

三、算法实践

1. 算法实现

• 输入数据（input）：11，34，20，10，12，35，41，32，43，14
• Java源代码

需要注意源代码与伪代码的区别，请查看文章开头补充的概念部分，这里不做过多说明。

public class SelectSort {

    public static void main(String[] args) {
        // input data
        int[] a = {11,34,20,10,12,35,41,32,43,14};
        // 调用选择排序
        sort(a);
        // 查看排序结果
        for (int data : a){
            System.out.print(data + "\\t");
        }
    }

    private static void sort(int[] a){
        // 外层循环用于控制循环的趟数
        for (int i = 0;i < a.length - 1;i++){
            int k = i;
            // 内层循环的作用是在无序区中选出最小的元素并记录
            for (int j = i + 1;j < a.length;j++){
                if (a[j] < a[k]) {
                    k = j;
                }
            }
            // 如果本轮选出的最小元素没有在对应的位置上则交换
            if (k != i){
                int tmp = a[i];
                a[i] = a[k];
                a[k] = tmp;
            }
        }
    }

}

• 执行效果

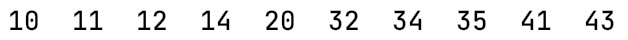
• 输出数据（output）：10，11，12，14，20，32，34，35，41，43

2. 时间复杂度

了解了算法的核心思想后可以发现，整体的排序趟数（外循环）与每趟排序中的元素比较次数（内循环）均和序列的初始顺序无关，因此时间复杂度T(n)=$\frac{n(n-1)}{2}$=O($n^2$)。

3. 空间复杂度

算法在执行过程中只需要定义的几个临时变量，所以空间复杂度为常数级：O(1)。

扫描下方二维码，加入官方粉丝微信群，可以与我直接交流，还有更多福利哦~