深度学习中的损失函数
Posted Terry_dong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习中的损失函数相关的知识,希望对你有一定的参考价值。
目录
1. 均方误差(Mean Square Error,MSE)
2. 平均绝对误差( Mean Absolute Error,MAE)
二分类损失(Binary Classification Loss)
1. 二元交叉熵损失(Binary Cross-Entropy Loss)
多分类损失(Multi-Class Classification Loss)
1. 多分类交叉熵损失(Multi-Class Cross-Entropy Loss)
二分类、多分类和回归损失函数详细介绍
深度学习(tensorflow)中的所有学习算法都必须 有一个 最小化或最大化一个函数,称之为损失函数(loss function),或“目标函数”、“代价函数”。损失函数是衡量模型的效果评估。比如:求解一个函数最小点最常用的方法是梯度下降法(比如:全批量梯度下降 Batch GD、随机梯度下降 SGD、小批量梯度下降 mini-batch GD、Adagrad法,Adadelta法、Adam法等)。损失函数就像起伏的山,梯度下降就像从山上滑下来到达最底部的点。
显然,不存在一个损失函数可以适用于所有的任务。损失函数的选择需要取决于很多因素,其中包括异常值的处理、深度学习算法的选择、梯度下降的时间效率等。本文的目的介绍损失函数,以及它们的基本原理。
损失函数严格上可分为两类:分类损失和回归损失,其中分类损失根据类别数量又可分为二分类损失和多分类损失。在使用的时候需要注意的是:回归函数预测数量,分类函数预测标签。
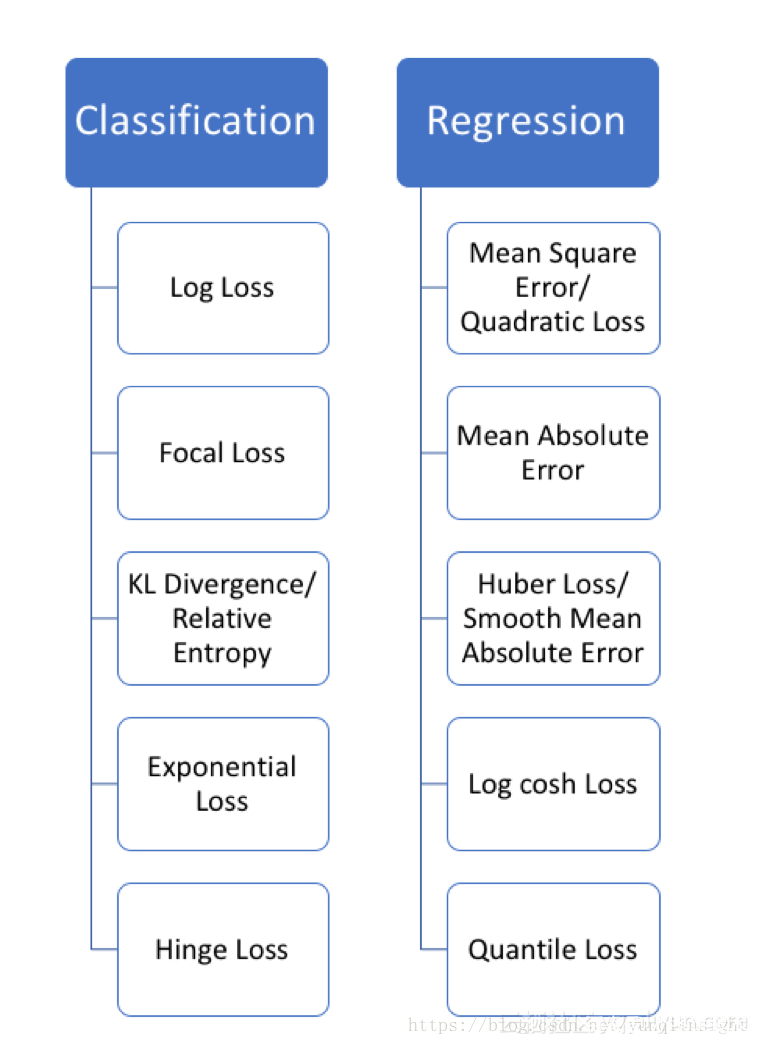
编辑搜图
损失函数集合
回归损失(Regression Loss)
1. 均方误差(Mean Square Error,MSE)
也可以称为二次损失(Quadratic loss) / L2损失(L2 Loss)
均方误差(MSE) 是常用的 回归类损失函数,表示的:预测值和真实label的距离平方和;公式如下:
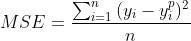
2. 平均绝对误差( Mean Absolute Error,MAE)
也称为 L1 损失(L1 loss)
平均绝对误差(MAE)也是一个回归模型的损失函数。MAE是预测值和真实值之间的绝对差之和(而均方误差需要平方和)。故而,它表示的是预测值的的平均误差大小,而不考虑方向,范围是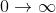 。若考虑到方向,那就会被定义为平均偏差(Mean Bias Error,MBE),它是残差/误差的总和。公如下:
。若考虑到方向,那就会被定义为平均偏差(Mean Bias Error,MBE),它是残差/误差的总和。公如下:
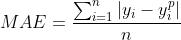
3. MSE 和MAE对比:
使用平方误差MSE更容易收敛,但使用绝对误差MAE对异常值更稳健
训练一个模型的时候,目标是为了找到损失函数取最小值的点。当预测值与真实label完全相等时,两个函数都会达到最小值。下面是两种损失函数的python代码,可以编写自己的函数,也可以使用sklearn的内置函数:
def mse(true, pred):
return np.sum((true - pred)**2)
def mae(true, pred):
return np.sum(np.abs(true - pred))
# also available in sklearn
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
从公式中可以看出,MSE和MAE 主要的区别是在于 预测值和真实label值之间差值 是否需要平方。当数据中出现一个非常大的异常值(离群值),这就会导致MSE 损失函数非常大。这样会导致 MSE损失模型比有MAE损失模型给离群点更多的权重。这回降低模型的整体性能。
很显然 训练数据如果被异常值破坏(例如,我们在训练环境中错误地接收到巨大的负/正值,而不是在测试环境中),推荐使用MAE损失函数。
直观的理解:1. 我们需要对所有试图使MSE最小化结果给出一个预测,那么这个预测结果是所有目标值的平均值。2. 我们最小化MAE的时候,这个预测结果是所有观测值的中值。现实中 中值会比均值对离群值更稳健,这使得MAE比MSE对离群值更稳健。
MAE损失函数的会存在一个比较大问题是,它的梯度在训练的时候一直是相同的,这也表明即使损失治很小,梯度也会非常大,这对学习没有好处。为了解决这个问题,需要设置动态学习率,这样随着训练的进行会接近最小值对时候学习率降低。MSE表现得很好,即使设置固定学习速率,也会进行收敛。当损失值越大,MSE损失的梯度越大,当损失接近0时,MSE损失的梯度越小,使得训练结束时MSE损失的梯度更精确(见下图)。
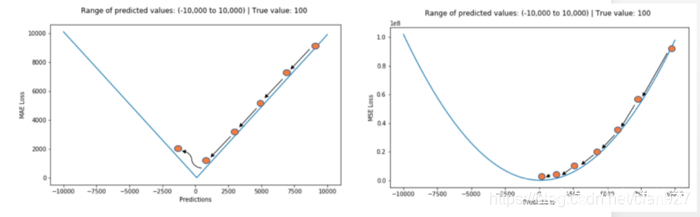
MSE和MAE学习率
如果选择使用哪个损失函数
1. 如果异常值代表的异常数据对业务是非常重要的,而且需要被检测到,应该使用MSE损失函数。2. 如果离群值仅仅代表损坏(噪声)的数据,应该选择MAE作为损失。
以上两个损失函数都可能存在的问题:都不能给出理想预测结果。例如,如果我们的数据中90%的真实label为150,其余10%的label在0~30之间。若 MAE作为损失的模型预测所有观测值为150,MAE会忽略10%的异常数据,因为MAE会向中值靠拢。在同样数据情况下,MSE的模型的预测值会在0到30的范围内,因为它会倾向于离群值。这两种结果在实战场景下都是不可取的。
那该怎么办?一个简单的解决方法是修改目标变量。另一种方法是尝试其他的损失函数。这就是需要提到第三个损失函数,Huber Loss背后的动机。
4.Huber Loss
也可以称为:Smooth Mean Absolute Error
与平方误差损失相比较,Huber Loss对数据中的噪声(异常值)不敏感。在0处也是可微的。Huber Loss 基本上算是绝对误差,当误差很小的时候就变成了二次方值(下面公式可以看出)。误差有多小时,Huber Loss 会变成二次方值 取决于超参数,这个超参数是需要手动调整的。Huber损失在时接近MSE,在(大数值)时接近MAE。公式如下
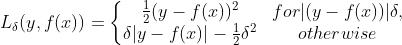
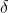 的设置 是很重要的,
的设置 是很重要的,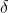 直接决定了 哪些数据为异常值(噪声)。大于
直接决定了 哪些数据为异常值(噪声)。大于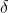 的误差 在L1中最小(L1对大的异常值(噪声)不那么敏感),而小于
的误差 在L1中最小(L1对大的异常值(噪声)不那么敏感),而小于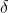 的残差在L2中较小。
的残差在L2中较小。
为什么要使用 Huber Loss
使用MAE训练神经网络的一个大问题是它的持续大梯度,这可能会导致在使用梯度下降训练结束时丢失最小值。对于MSE,当损失接近其最小值时,梯度减小,使其更加精确。
在这种情况下,Huber损失是非常有用的,因为它在减小梯度的最小值附近弯曲。它比MSE对离群值更稳健。因此,它结合了MSE和MAE的优良性能。然而,Huber损失的问题是我们可能需要训练超参数delta,这是一个迭代过程。
5. Log-Cosh Loss
Log-Cosh是一个回归损失函数,它比L2更平滑的损失函数。Log-cosh是预测误差使用的数学函数是双曲余弦的对数。公式如下:
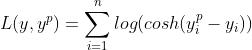
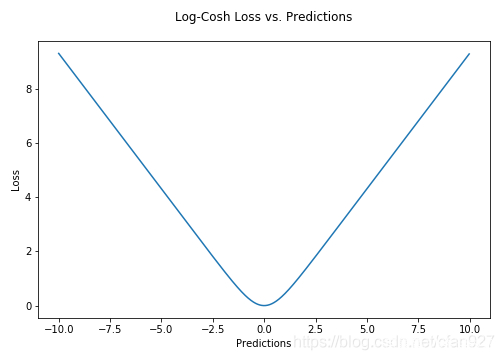
优点: 1. 该损失函数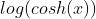 数学意义近似 (x^2)/2;其中,对于非常大的x 数学意义近似于
数学意义近似 (x^2)/2;其中,对于非常大的x 数学意义近似于 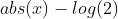 ;这里的数学意义表明:该函数的工作方式与均方差公式有点类似,该损失函数,具有Huber损失函数的所有优点,并且处处可微。
;这里的数学意义表明:该函数的工作方式与均方差公式有点类似,该损失函数,具有Huber损失函数的所有优点,并且处处可微。
为什么需要二阶导数?许多ML模型实现如XGBoost使用牛顿法来寻找最优值,这就是为什么需要二阶导数(Hessian)。对于像XGBoost这样的ML框架,两次可微函数更合适。

xgboost 二阶导数,公式
但是该损失函数也存在一些缺点。它对于一些非常大的噪声(离群点)的预测是恒定的。还是会受到梯度和Hessian问题的干扰,所以也会导致XGBoost缺少分割。
6. 分位数损失(Quantile Loss)
在预测问题中,我们会更关注数据中预测出来的 不确定性数据感兴趣。熟悉预测的范围,不单单只是预测值。在很多业务上的决策问题都会有帮助。
分位数损失函数(Quantile Loss)在需要进行预测结果为一个区间时候是一个非常有用的工具。一般情况下利用最小二乘回归模型来预测取值区间,基于的假设:取值残差的方差是常数。但是很多时候数据是不满足该假设的。这就需要分位数损失函数和分位数回归模型去优化回归模型了。该模型对于预测的区间是非常敏感的,即使在非均匀分布的残差下也可以保持较好的性能。用两个图片看看分位数损失函数 在异方差数据下的回归表,下面两幅图做了个对比:
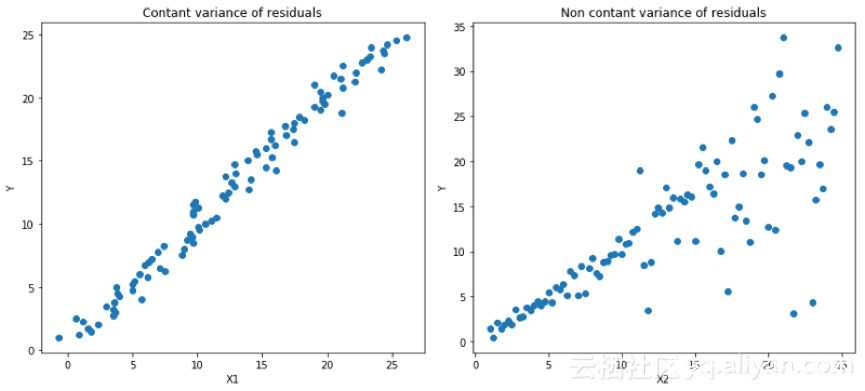
左:线性关系b / w X1和Y.具有恒定的残
上图是两种不同的数据分布,其中上面的左图是残差的方差为常数的情况,而上面右图则是残差的方差随着x 进行 变化的情况(不是常数)。利用正常使用的最小二乘模型对上述两种情况进行了预测,下图中中间橙色线为建模的结果。但却无法得到取值的区间,这就需要分位数损失函数来解决该问题了。
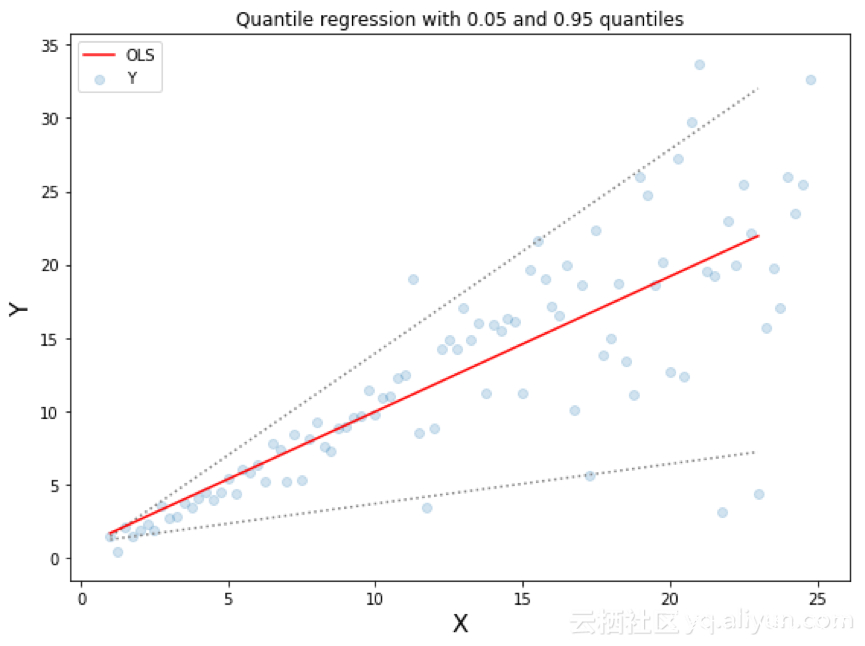
两条虚线基于0.05和0.95的分位数损失
基于分位数 的回归模型是在 预测变量 是确定值的情况下去估计响应变量的条件分位数。分位数损失函数 可以看作是MAE的一个扩展类型(当分位数是50%时,形式就是MAE)。
选择分位数值的思想 是需要基于 业务上需求确定 ,需要给正误差更多的值还是 相反给负误差更多的值。分位数误差损失函数试图根据所确定的分位数的值,对高估和低估给予不同的惩罚。例如,分位数损失函数( )对过高估计预测值给予更多惩罚,并保持预测值略低于中值。
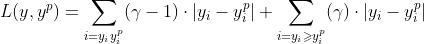
γ是分位数,其值在0和1之间。
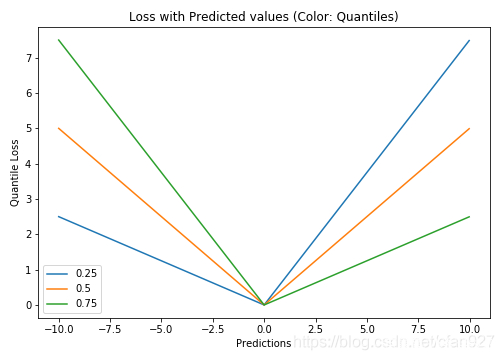
明显可以看到对于正负误差不平衡的状态
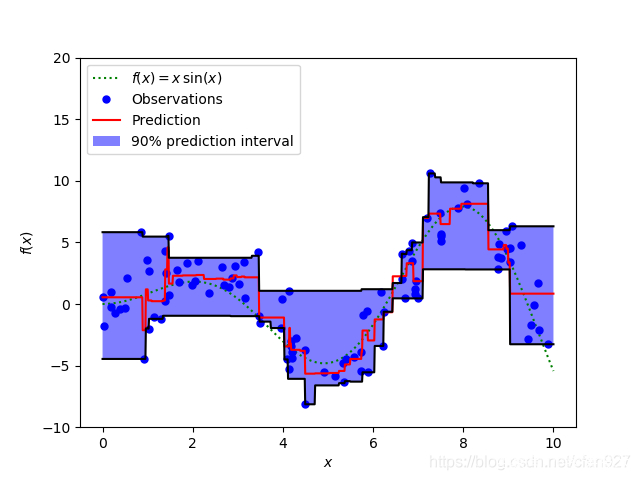
Sklearn实现梯度增强树回归
上图显示了sklearn库的GradientBoostingRegression中可用的分位数损失函数计算出的90%的预测区间。上界构造为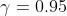 ,下界构造为
,下界构造为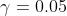
最后做个对比实验:利用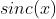 模拟出数据进行对不同损失函数的性能和效果进行了比较。并且在原始
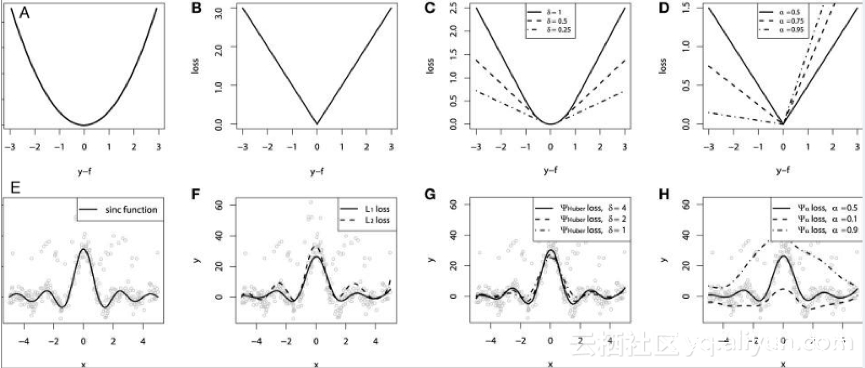
模拟出数据进行对不同损失函数的性能和效果进行了比较。并且在原始 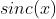 数据中 融合了 高斯噪声和脉冲噪声(基于鲁棒性实验进行比对)。下图是GBM回归器模型利用上面提到的不同损失函数得到的实验结果。下图 中的ABCD图分别是MSE, MAE, Huber, Quantile损失函数的结果:
数据中 融合了 高斯噪声和脉冲噪声(基于鲁棒性实验进行比对)。下图是GBM回归器模型利用上面提到的不同损失函数得到的实验结果。下图 中的ABCD图分别是MSE, MAE, Huber, Quantile损失函数的结果:
编辑搜图
请点击输入图片描述(最多18字)
简要说明:E图:一个平滑的GBM拟合成有噪声的sinc(x)数据,是原始函数;F 图:是符合MSE损失函数和MAE损失函数的平滑GBM;G图:是平滑GBM,其具有Huber损失函数,δ= {4,2,1};H图:光滑的GBM 与α= {0.5,0.1,0.9}的分位数损失函数。
总结:1. MAE损失函数受到冲击噪声的影响最小,2. 而MSE损失函数有一定的偏差;3. Huber损失函数对于超参数的选取不是狠敏感 ;4.分位数损失函数在对应的置信区间内得到比较好的效果。
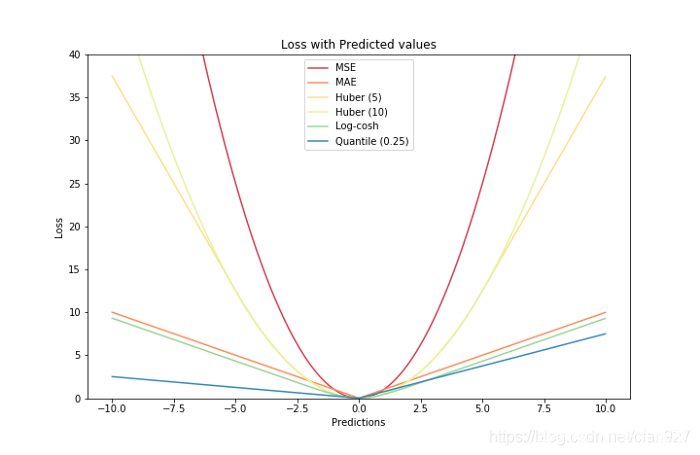
7.损失函数对比:
将所有的损失函数绘制在一张图上。
二分类损失(Binary Classification Loss)
1. 二元交叉熵损失(Binary Cross-Entropy Loss)
熵 : 表示一个事件的无序或不确定性,它是对概率分布为p(X)的随机变量X进行测量。公式如下:
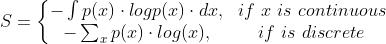
概率分布的熵越大,表明该数据分布的不确定性也就越大。同样,概率值越小,分布越确定,不确定性也就越小。
这使得二元交叉熵最适合当作损失函数来最小化它的损失值。对于输出概率为p的分类任务重,可以使用二元交叉熵损失函数来进行训练模型。
2. 铰链损失(Hinge Loss)
Hinge Loss 损失函数 需要和 分类标签label为-1和1 的支持向量机(SVM)分类器模型一起使用。重点:需要确保数据集中的负类的标签label从0更改为-1。
Hinge损失不仅会惩罚错误的预测,也会惩罚不确定的正确预测。
Hinge Loss损失函数的公式:
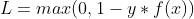
def update_weights_Hinge(m1, m2, b, X1, X2, Y, learning_rate):
m1_deriv = 0
m2_deriv = 0
b_deriv = 0
N = len(X1)
for i in range(N):
# Calculate partial derivatives
if Y[i]*(m1*X1[i] + m2*X2[i] + b) <= 1:
m1_deriv += -X1[i] * Y[i]
m2_deriv += -X2[i] * Y[i]
b_deriv += -Y[i]
# else derivatives are zero
# We subtract because the derivatives point in direction of steepest ascent
m1 -= (m1_deriv / float(N)) * learning_rate
m2 -= (m2_deriv / float(N)) * learning_rate
b -= (b_deriv / float(N)) * learning_rate
return m1, m2, b使用三种不同的alpha值运行上面的代码 ,并经过2000次迭代后的效果图如下:
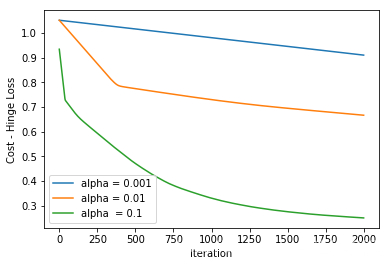
Hinge-Loss 损失函数 效果图
Hinge-Loss损失函数 简化了支持向量机的数学运算过程,但是也 使的模型的损失最大化(与对数损失相比)。当业务中需要做出实时决策却不需要提高准确性时,Hinge-Loss可以选择使用。
多分类损失(Multi-Class Classification Loss)
1. 多分类交叉熵损失(Multi-Class Cross-Entropy Loss)
多分类交叉熵损失函数是二元(二分类)交叉熵损失函数的推广形式。输入向量和对应的单编码目标向量的损失函数;
somftmax函数:可以用来求解概率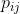 :最终softmax会给出最大概率的类别。
:最终softmax会给出最大概率的类别。
tf2.0的代码如下:指定使用损失函数:categorical_crossentropy
# importing requirements
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import adam
# alpha = 0.001 as given in the lr parameter in adam() optimizer
# build the model
model_alpha1 = Sequential()
model_alpha1.add(Dense(50, input_dim=2, activation='relu'))
model_alpha1.add(Dense(3, activation='softmax'))
# compile the model
opt_alpha1 = adam(lr=0.001)
model_alpha1.compile(loss='categorical_crossentropy', optimizer=opt_alpha1, metrics=['accuracy'])
# fit the model
# dummy_Y is the one-hot encoded
# history_alpha1 is used to score the validation and accuracy scores for plotting
history_alpha1 = model_alpha1.fit(dataX, dummy_Y, validation_data=(dataX, dummy_Y), epochs=200, verbose=0)经过200个迭代训练后的效果图:
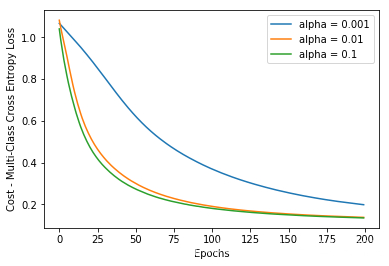
训练200次的loss
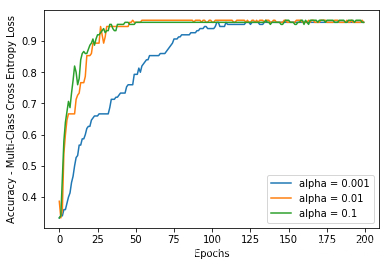
训练200次的accuracy
2. KL散度(KL-Divergence)
Kullback-Liebler散度:一个数据的概率分布与另一个数据的概率分布差异的数学度量,若KL散度为零则表示两个数据的分布是相同的。

KL酸度的公式
但是需要注意的是:KL散度函数是不对称的。所以KL散度不能用作距离度量。
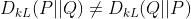
KL散度 介绍:作为损失函数的方法,不深入探讨数学原理。KL散度是不对称的,用两种方法,公式下:
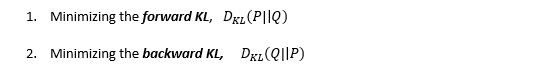
编辑搜图
KL散度 两种方法
第一种方法主要用于监督学习案例中,第二种方法主要用于强化学习案例中。KL散度公式类似于多类交叉熵,所以也称为P相对于Q的相对熵:
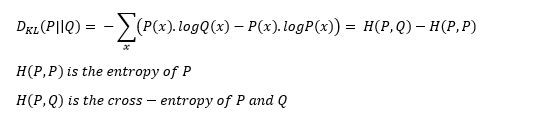
编辑搜图
KL散度的解析
在tf2.0 代码中使用 compile()函数中,并且指定 kullback_leibler_divergence 作为损失函数参。代码如下:
# importing requirements
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import adam
# alpha = 0.001 as given in the lr parameter in adam() optimizer
# build the model
model_alpha1 = Sequential()
model_alpha1.add(Dense(50, input_dim=2, activation='relu'))
model_alpha1.add(Dense(3, activation='softmax'))
# compile the model
opt_alpha1 = adam(lr=0.001)
model_alpha1.compile(loss='kullback_leibler_divergence', optimizer=opt_alpha1, metrics=['accuracy'])
# fit the model
# dummy_Y is the one-hot encoded
# history_alpha1 is used to score the validation and accuracy scores for plotting
history_alpha1 = model_alpha1.fit(dataX, dummy_Y, validation_data=(dataX, dummy_Y), epochs=200, verbose=0)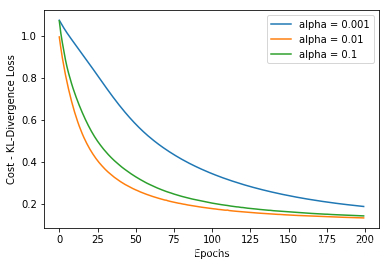
KL散度的 loss
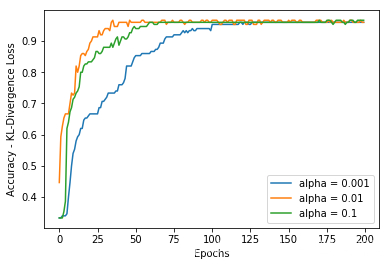
KL散度的 acuraccy
相比多类分类任务,KL-散度 常用于近似复杂函数。 深度自动生成模型(如变分自动编码器(VAE))会经常用到KL-散度函数。
以上是关于深度学习中的损失函数的主要内容,如果未能解决你的问题,请参考以下文章