逻辑回归算法检测java_meterpreter

Posted 2021-06-12 Neil-Yale

本次实验我们来学习使用逻辑回归算法来检测java meterpreter.
先来学习逻辑回归算法
首先需要搞懂逻辑回归与线性回归（Linear Regression）的区别，虽然二者都带有“回归”二字，但是用来解决不同的问题。线性回归解决“回归”问题，用一条直线来拟合所有的点，例如探究某超市的销售额与小区常住人口数的关系；而逻辑回归则解决“分类”问题，例如可预测一封邮件是否为垃圾邮件，预测客户是否会发生债务违约等。
逻辑回归算法分三步进行，首先，我们需要确定一个预测函数，即预测出一个值来判断归属哪一类，可定义预测值大于某个阈值判断为一类，反之为另一类；第二步，为了计算参数，我们需要定义一个损失函数，损失函数用来衡量真实值和预测值之间的差异，这个差值越小说明预测效果越好；第三步，用梯度下降法计算参数，使损失函数不断减小，得出参数后，带入预测函数就可以来进行预测了。
一、寻找预测函数h(x)

1. 预测函数的形式
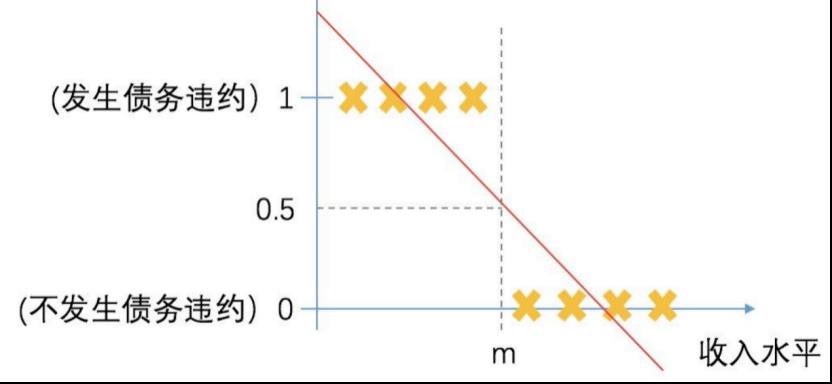
   线性回归的预测函数是一条直线，那么逻辑回归的预测函数能否也用一条直线呢？我们假设要预测一个客户是否会发生债务违约，客户的很多特征与因变量相关，以收入为例，通常来讲客户的收入水平越高，其发生债务违约的可能性越低。假如预测函数是线性的，找一条直线拟合所有点如图中的红线所示，通过设定一个阈值（假设0.5），可以较好地将两类客户分开，若客户的收入水平大于m，预测函数预测出的结果大于0.5，则判定客户不会违约；若客户的收入水平小于m，预测值小于0.5，则判定会违约，这样的分类效果令人满意。
   

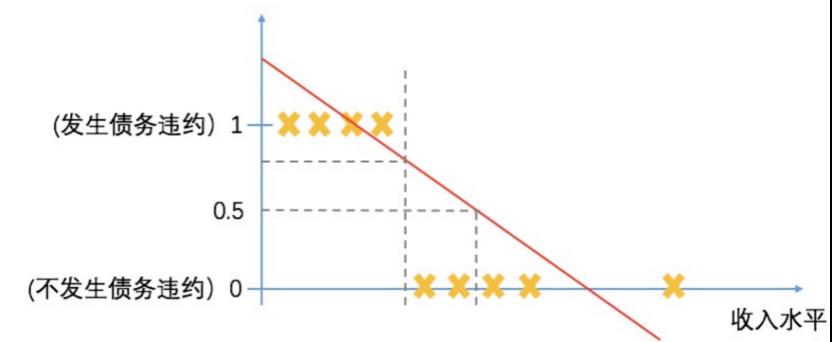
线性的预测函数的缺点是对“异常值”敏感，例如样本中加入了新的客户，其收入水平非常高，且没有发生违约，拟合出新的直线如图中的黄线所示，如果还想将二者完美区分的话，选取的阈值就不能是0.5了，若还是0.5，会将一部分优质客户错误预测为会发生违约。基于线性预测函数对异常值敏感的特性，我们需要针对分类问题探索一种新的预测函数

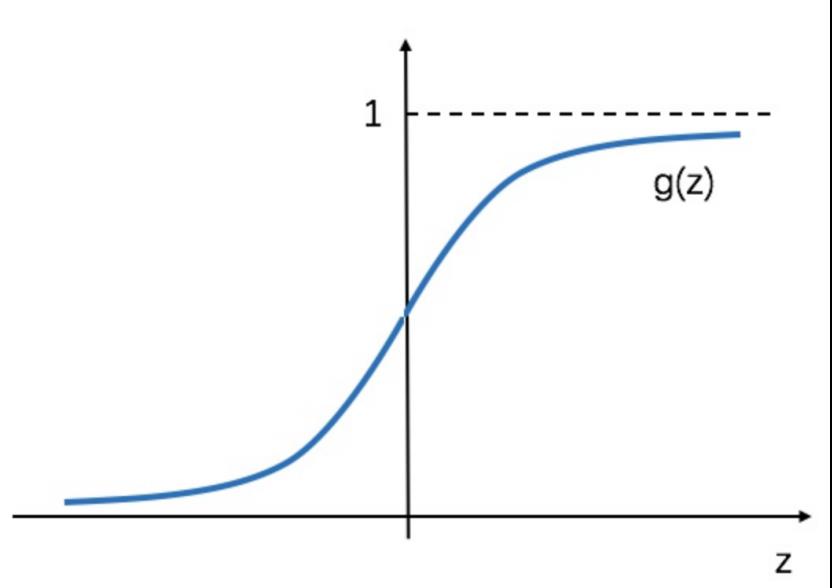
sigmoid函数g(z)似乎满足我们的需求，当x趋近于+∞时，y无限趋近于1，而当x趋近于-∞时，y无限趋近于0，有异常值出现时，sigmoid函数能够做出正确的判断。由于sigmoid函数可以将x的值映射到0到1之间，它可以表示预测的概率，假如预测值是0.75，那么客户属于第1类（违约）的概率为75%，不违约的概率为25%。

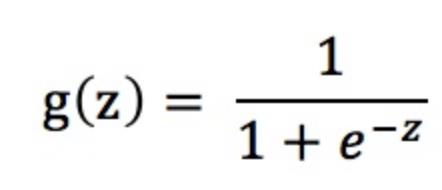
2. 决策边界

为了确定预测函数，我们需要引入一个新的概念——决策边界（Decision Boundary），以二元变量为例，决策边界是将两类客户最大程度地区分开，若可以用一条直线将两类区分，即存在线性的决策边界，反之为非线性决策边界，例如图中的圆

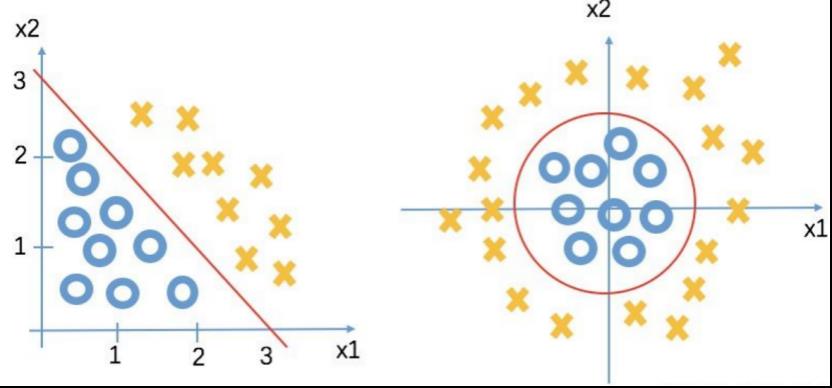
图中的直线可以用x1+x2=3来表示，x1+x2>3表示的是右上部分，即正样本，x1+x2<3表示图中的左下部分，即负样本，利用x1、x2两个变量的值即可判断正负样本，将结果映射到[0, 1]之间即可预测概率，这个映射的过程可以用上述sigmoid函数的形式。

线性边界的边界形式为：

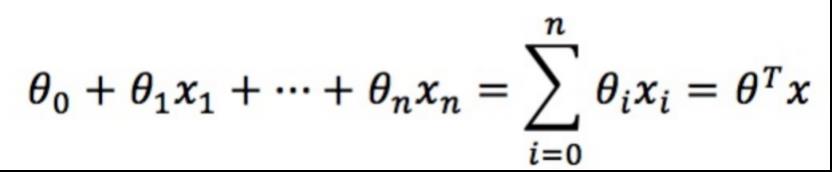
将其映射到[0, 1]，即可得出预测函数的形式为：

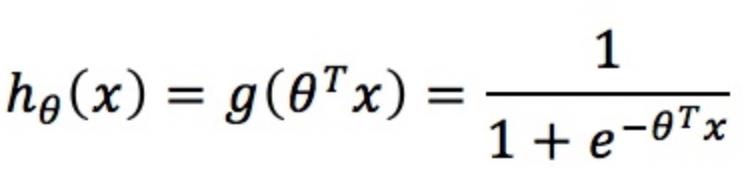
二、构造损失函数J(θ)
现在我们需要求解参数θ，逻辑回归中运用的是梯度下降法，首先定义一个损失函数J(θ)，不断更新θ使得损失函数不断减小，当损失函数下降的值小于阈值时，就停止更新，即可得出参数。
损失函数表示的是真实值和预测值之间的差异，可以表示为：

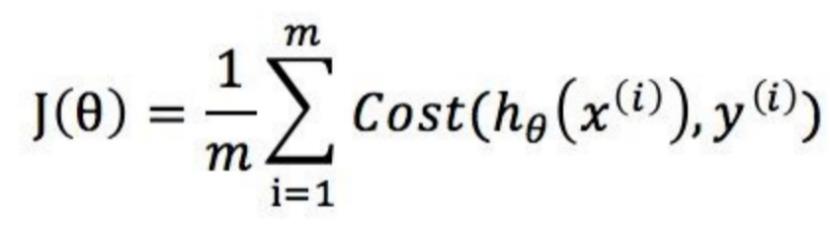
其中m表示样本的数量。
构造理想的损失函数，当y=1时，预测函数越接近1，损失函数值越小，反之越大；当y=0时，预测函数越接近1，损失函数值越大，反之越小。那么Cost函数可以表示为:

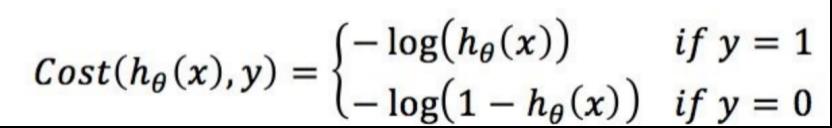
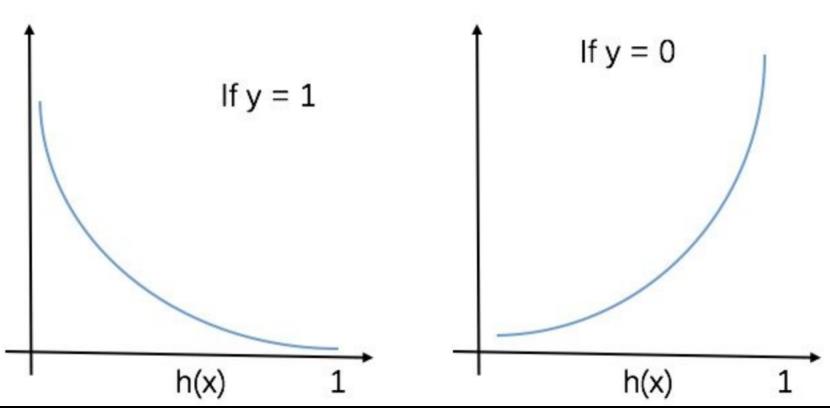
将Cost函数简化：

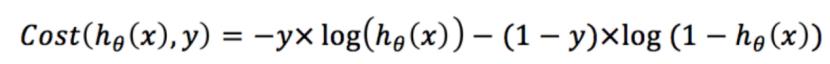
带入J(θ)中，即可得到损失函数：

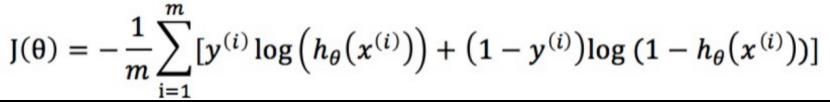
三、梯度下降法求解参数θ
有了损失函数J(θ)，我们就可以求解参数θ了，要令损失函数最小化，我们定义更新函数为（α为步长）：

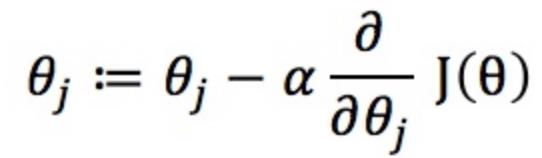
求偏导的部分简化步骤如下：

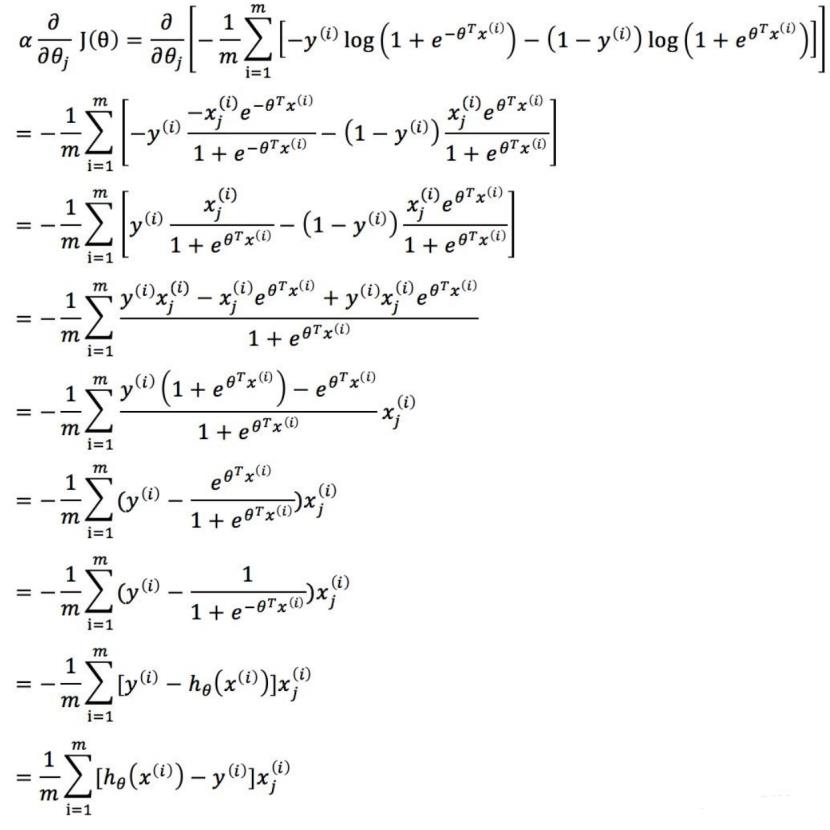
那么更新过程可表示为：

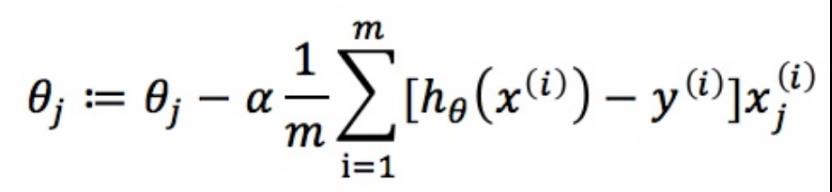
将每一次更新迭代得出的θ带入J(θ)，即可得出损失函数的值，求出损失函数值，与上一次迭代的损失函数值相减，结果小于阈值就停止迭代，这样损失函数不断下降，就求解出了θ。

θ的求解过程是迭代的过程，从初始值开始迭代，使得损失函数下降，预测的准确度提升，直到预测没有提升就停止迭代，得出参数结果。
参数的实际含义是什么呢？用债务违约的例子来说，θ表示当客户的收入每减少1元，其债务违约的概率提升θ%。
经过上述三步，整个逻辑回归的算法过程就结束了，我们首先定义了预测函数h(x)，构造了损失函数J(θ)，利用梯度下降法更新θ，使得损失函数的值不断下降，当停止优化时，即可求解出θ，将参数θ带入预测函数中，我们就可以开始进行预测了。
当然实际在应用的时候并没有这么繁琐，各种机器学习框架都有封装好的函数可以直接使用。
接下来我们看看在scikit中是如何使用逻辑回归算法的

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
clf = LogisticRegression(random_state=0).fit(X, y)
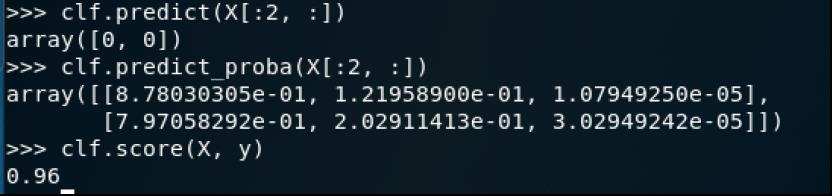
clf.predict(X[:2, :])
array([0, 0])

clf.predict_proba(X[:2, :])
array([[8.78030305e-01, 1.21958900e-01, 1.07949250e-05],
[7.97058292e-01, 2.02911413e-01, 3.02949242e-05]])

clf.score(X, y)
0.96
加载相关库文件和自带的iris数据集

调用逻辑回归算法进行训练

可以使用predict预测X中样本的类别标签，使用predict_proba估计概率，使用score打印给的测试数据和标签上的平均准确率

本次实验用到的数据集来自ADFA-LD。ADFA-LD数据集分为三组，每一组都包含了原始系统调用顺序。
每个训练集（Training_Data_Master）和验证集（Validation_Data_Master）的数据都是在主机的正常操作过程中收集的，包括从浏览web到准备latex文档的各种活动。调用序列通过auditd Unix程序生成，然后按大小进行过滤。
其中训练集数据大小在300比特到6kb之间，验证集数据在300kb到10kb之间，这是为了有效权衡数据保真度和不必要的处理负担。
攻击数据集（Attack_Data_Master）里共有6种攻击方式，我们之前使用过webshell，这次来使用java-meterpreter
选中任一txt打开内容如下

ADFA数据集已经对系统调用进行了处理，所以对于每一个系统调用函数，ADFA都已经用数字来编号了。对应的编号见ADFA-LD+Syscall+List.txt文件，如下所示

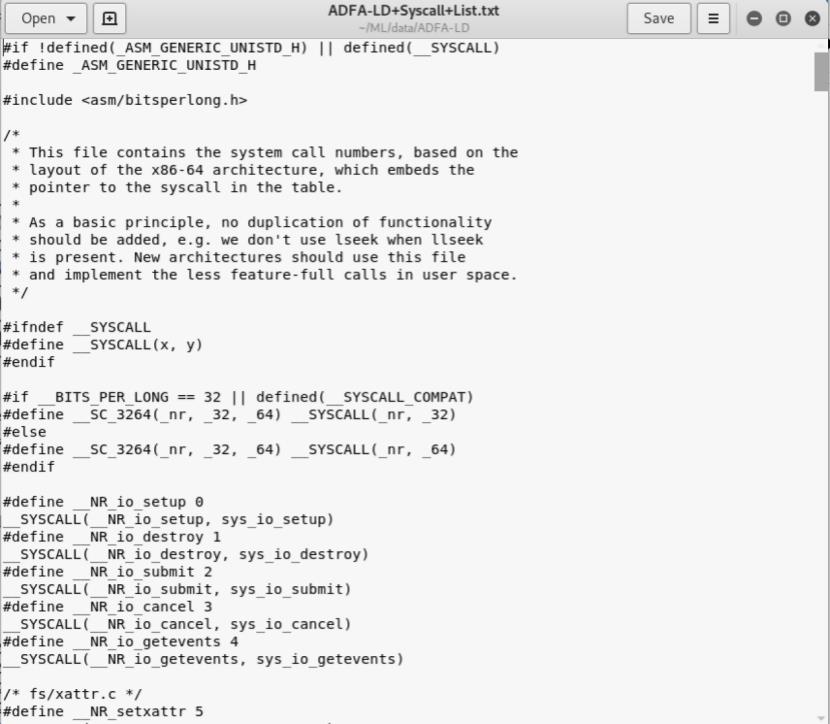
我们可以对数据集进行简单的分析，方法有很多，比如可以从词模型角度看样本集中不同类别label的数据中是否存在公共模式，这一步本质上是在考虑样本数据集是否线性可分，即样本中包含的规律真值是否足够明显，只有数据集本身是线性可分的，才有可能通过算法建模分析。样本集中的syacall本质上就是一个词序列，我们将其2-gram处理，统计词频直方图

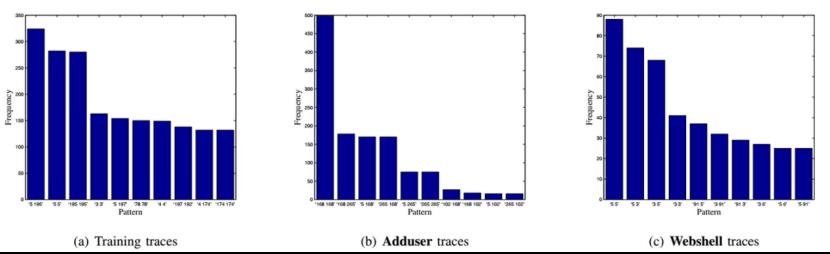
我们发现，在Adduser类别中，“168 168”、“168 265”这2个2-gram序列出现的频次最高，而在Webshell类别中，“5 5”、“5 3”这2个2-gram出现的频次最高。这从一定程度上表明两类数据集在2-gram词频这个层面上是线性可分的
我们既然已经知道这些数据既然本质是词序列，那么我们可以考虑使用词袋模型（BoW）或者词集模型（SoW）
Set-of-Words词集模型是单词构成的集合，每个词的数量表示有多种方法:可以表示为0-1(在这篇文章中,这个词出现了没有),词频(在这篇文章中,这个词出现了多少次)
Bag-of-Words词袋模型,经常用在自然语言处理和信息检索当中.在词袋模型中,一篇文本被表示成"装着词的袋子",也就是说忽略文章的词序和语法,句法;将文章看做词的组合,文中出现的每个词都是独立的,不依赖于其他词.虽然这个事实上并不成立,但是在实际工作中,效果很好.

可以简单看看scikit中的CountVectorizer函数实现的BoW，我们在后面的代码中也会用到。此处的代码在bow.py

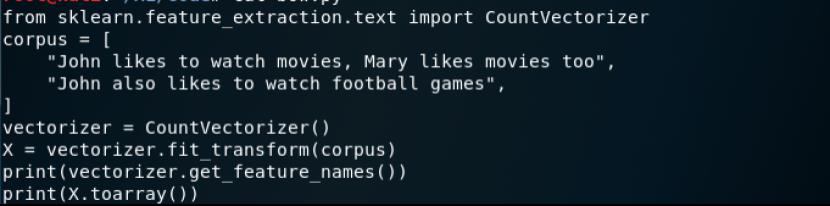
通过fit_transform函数计算各个词语出现的次数，通过get_feature_names()可获取词袋中所有文本的关键字，通过toarray()可看到词频矩阵的结果
运行结果如下

接下来我们写代码
下图的三个函数依次用于加载文件内容，加载ADFA-LD中的正常样本数据，遍历指定目录下的文件

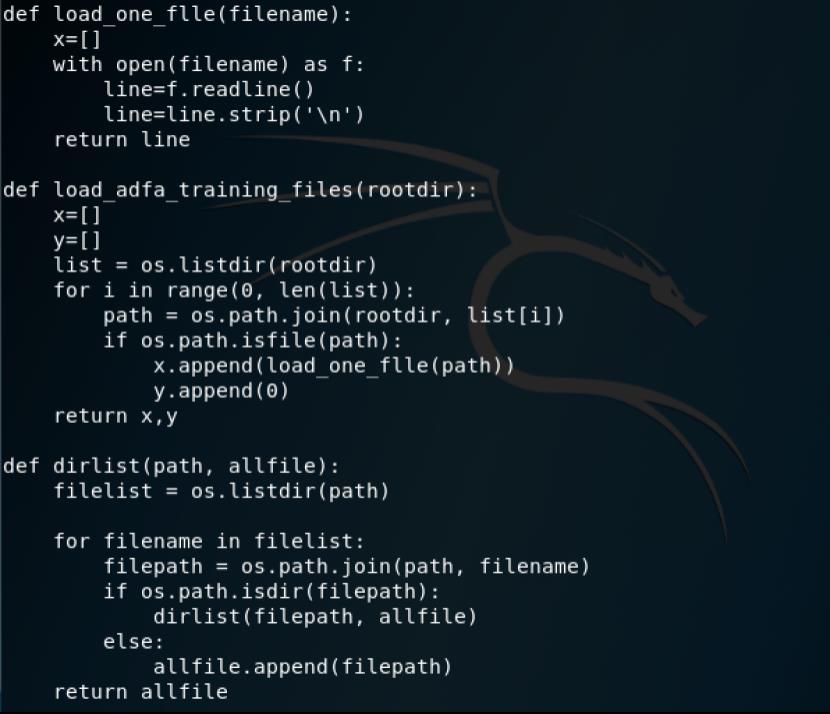
以及从攻击数据集中加载和java meterpreter攻击相关的数据集

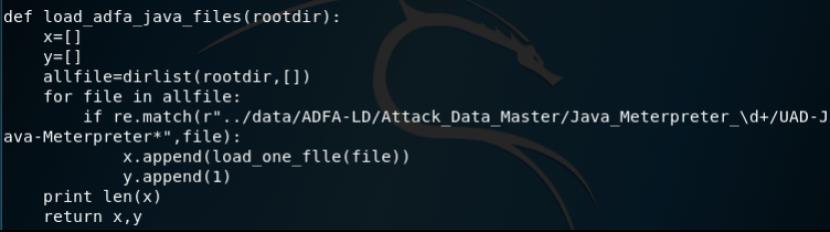
然后就是调用前面写好的函数进行加载

接下来采用词集模型进行特征化

这里的CountVectorizer类会将文本中的词语转换为词频矩阵，例如矩阵中包含一个元素a[i][j]，它表示j词在i类文本下的词频。它通过fit_transform函数计算各个词语出现的次数，通过get_feature_names()可获取词袋中所有文本的关键字，通过toarray()可看到词频矩阵的结果
调用逻辑回归算法进行训练，并采用10折交叉验证，打印准确率

脚本运行后如下所示

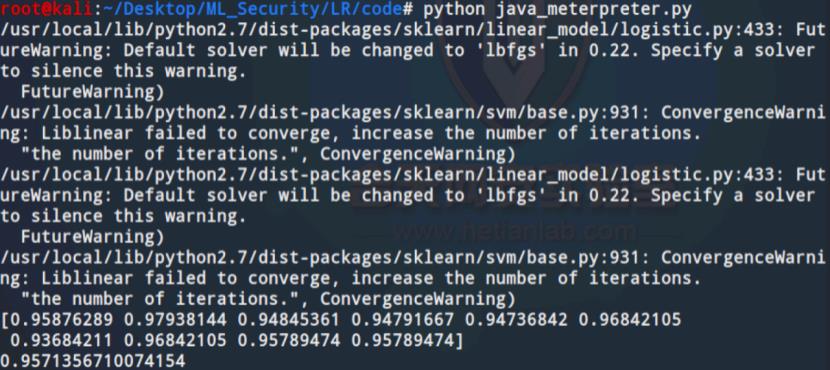
可以看到准确率达到了95%左右。

参考：
1.https://www.zuozuovera.com/archives/918/
2.https://www.jiqizhixin.com/articles/2018-05-13-3
3.https://www.cnblogs.com/LittleHann/p/7806093.html#_lab2_1_2
4.https://zhuanlan.zhihu.com/p/63487235
5.《机器学习与web安全》
6.https://github.com/duoergun0729/1book/