LeetCode 1486.数组异或操作

Posted 2021-06-12 龚喜发财+1

题目描述：给你两个整数，n 和 start 。
数组 nums 定义为：nums[i] = start + 2*i（下标从 0 开始）且 n == nums.length 。
请返回 nums 中所有元素按位异或（XOR）后得到的结果。

题解1：暴力解法

int xorOperation(int n, int start)
{
    int result = start, i;
    for (i = 1; i < n; i++)
    {
        result = result ^ (start + i * 2);
    }
    return result;
}

题解2：数学解法

class Solution {
    public int xorOperation(int n, int start) {
        // 结果的最低位
        // 当n和start的最低位都为1时，lowestOrder=1，否则为0
        int lowestOrder = n & start & 1;
        
        // start ^ (start+2) ^ (start+4) ^ …… ^(start + 2*(n-1))
        //  =(令s=start/2)
        // (s ^ (s+1) ^ (s+2) ^ …… ^ (s+n-1)) * 2 + lowestOrder
        // 此处lowestOrder是为了补全start/2时丢失的1
        //start除以2相当于右移一位，而结果再左移一位，中间如果最后一位为0，则没有损失，若最后一位是1，则会发生损失，所以用b0补充
        int s = start / 2;
        
        // 而n到m(n<m)的异或等于1到n-1的异或 异或 1到m的异或
        // 原因：a^a = 0   0^a = a
        int result = computeXOR(s - 1) ^ computeXOR(s + n - 1);
        
        return result * 2 + lowestOrder;
    }

    int computeXOR(int n) {
        // 前n个数异或的结果是有规律的
        // 例如：   二进制数   异或结果    return
        //      1    0001    0001        1
        //      2    0010    0011       n+1
        //      3    0011    0000        0
        //      4    0100    0100        n
        //      5    0101    0001        1
        //      6    0110    0111       n+1
        //      ……   ……      ……
        switch(n % 4)
        {
            case 0:
                return n;
            case 1:
                return 1;
            case 2:
                return n + 1;
            // case3
            default:
                return 0;
        }
    }
}

（1）首先start为偶数时，不管n是奇数还是偶数结果的最后一位一定为0，start为奇数时，如果n为偶数，结果最后一位还是0，n为奇数时，最后一位一定为1。所以只有在n和start都为奇数时结果的最后一位才为1，其余情况都为0.
（2）(s)^(s+1)(s+2)^(s+3)…^(s+(n-1)) = (1²3^…(s-1)) ^ (1²3^…(s+n-1))
举例：3⁴5⁶7⁸9 = (1²⁾(1²3⁴5⁶7⁸9)

因为（1^2）(1^2)=0
**异或的运算法则：**记 ⊕ 为异或运算，异或运算满足以下性质：
x⊕x=0；
x⊕y=y⊕x（交换律）；
(x⊕y)⊕z=x⊕(y⊕z)（结合律）；
x⊕y⊕y=x（自反性）；
∀i∈Z，有4i⊕(4i+1)⊕(4i+2)⊕(4i+3)=0
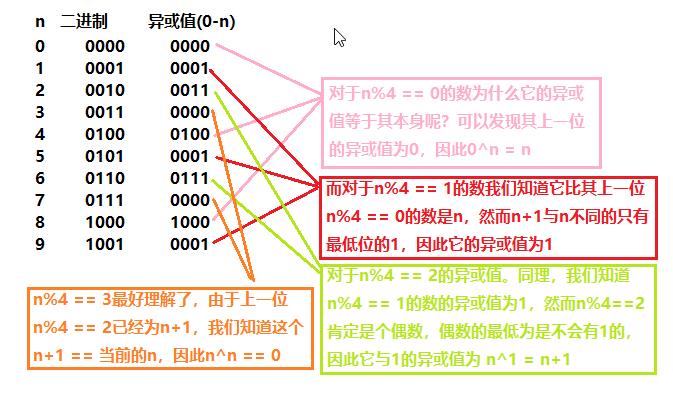
（3）