递归问题(斐波那契，青蛙跳台，汉诺塔)

Posted 2021-06-11 两片空白

文章目录

• 一.递归介绍
• • 1.什么是递归
  • 2.递归的两个必要条件
  • 3.递归优缺点
• 二.斐波那契数
• 三.青蛙跳台
• 四.汉诺塔

一.递归介绍

1.什么是递归

程序调用自身的编程技巧称为递归。递归作为一种算法在程序设计语言中广泛应用。递归通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。
递归主要的思考方式在于：把大事化小。

2.递归的两个必要条件

• 递归把大事化小同样满足原来的条件，才能实现自己调用自己。
• 存在限制条件，每次递归调用之后越来越接近这个限制条件，当满足限制条件的时候，递归不再继续。

举一个例子：
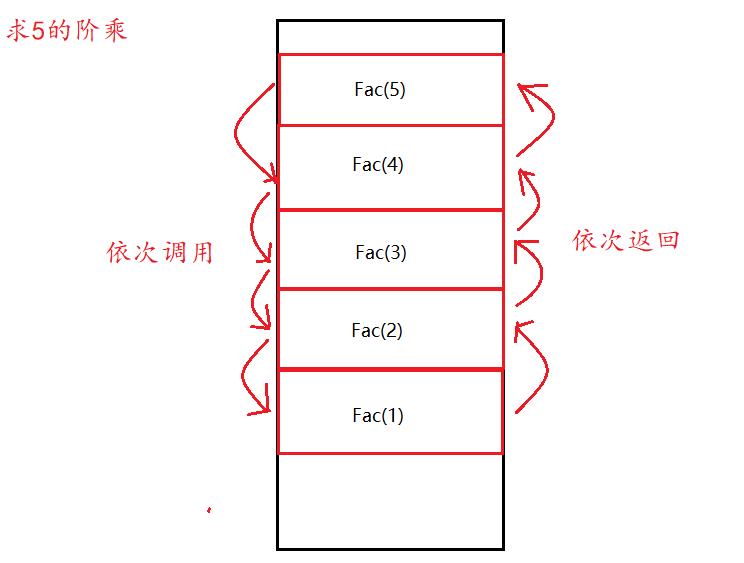
用递归的方法求n的阶乘(不考虑溢出)。
分析：
n!可以看作n*(n-1)！，(n-1)!又可以看作(n-1)*(n-2)!.. …依次往后推，可知到他们又一个共性就是都是求阶乘。当到最后时n=1时，阶乘等于1，这就是限制条件。

#include<stdio.h>
int Fac(int n){
	if (1 == n){//递归出口，限制条件
		return 1;
	}
	return n*Fac(n - 1);//有相同的共性，且大事化小。自己调用自己
}
int main(){
	int n = 0;
	scanf("%d", &n);
	int result = Fac(n);
	printf("%d\\n", result);
	return 0;
}

3.递归优缺点

优点：
1.许多问题都是由递归的形式进行解释的，因为他比非递归的形式更清晰。
2.但一个问题很复杂，往往递归的方式会使代码更简单。
缺点：
1.递归天然需要函数调用(形参栈帧)，当调用次数过多，势必会引起效率低下(时间),甚至栈溢出(空间）。

二.斐波那契数

问题描述：斐波那契数的前两个数等于1，从第三位开始为前两数之和。求第n个数的斐波那契数
例如：fib(5)=fib(4)+fib(3),fib(n)=fib(n-1)+fib(n-2).
共性都是求前两数的斐波那契数，限制条件，前两数等于1。

#include<stdio.h>
int Fib(int n){
	if (1 == n || 2 == n){
		return 1;
	}
	return Fib(n - 1) + Fib(n - 2);

}

int main(){
	int n = 0;
	scanf("%d", &n);
	int result = Fib(n);
	printf("%d\\n", result);
	return 0;
}

三.青蛙跳台

问题描述：青蛙跳台阶的方式由两种，一次性跳两层或者一次性跳一层。问，青蛙跳上n阶台阶有多少中方式。

共性都是求青蛙跳上台阶的有多少种方法，限制条件跳上第一层台阶有1种方式，跳上第二层台阶有2种方式。

#include<stdio.h>
int Jump(int n){
	if (1 == n){
		return 1;
	}
	if (2 == n){
		return 2;
	}
	return Jump(n - 1) + Jump(n - 2);

}
int main(){
	int n = 0;
	scanf("%d", &n);
	int result = Jump(n);
	printf("%d\\n", result);
	return 0;
}

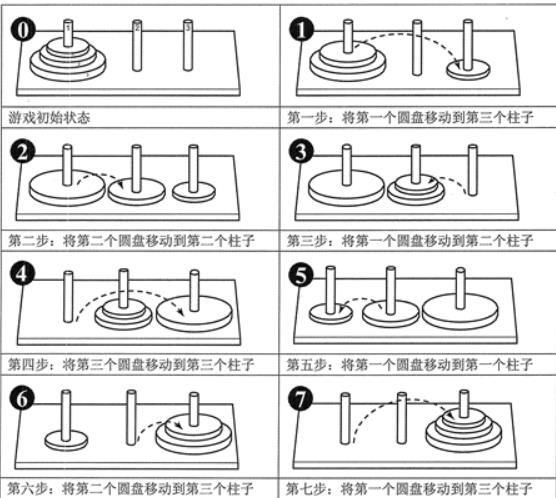
四.汉诺塔

问题描述：有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。求从A移到C要多少种方法。

分析：想法其实很简单，例如有n个圆盘在A柱上，首先要将n个圆盘上的n-1个圆盘移到一根柱子上，在将下面这个最大的圆盘移到目标柱子上，在将n-1个圆盘移到目标柱子上。即：Hano(n)=Hano(n-1)+1+Hano(n-1)。
共性都是求移柱子的方法，限制条件1个圆盘时只有1种方法。

#include<stdio.h>
int Hano(int n){
	if (1 == n){
		return 1;
	}
	return Hano(n - 1) + 1 + Hano(n - 1);
}
int main(){
	int n = 0;
	scanf("%d", &n);
	int result = Hano(n);
	printf("%d\\n", result);
	return 0;
}