路径规划基于A星和改进A星求解节点间的路径规划问题matlab源码

Posted 2021-06-11 Matlab咨询QQ1575304183

A* 算法是启发式搜索算法，是根据Dijkstra算法改进而来。

问题引入

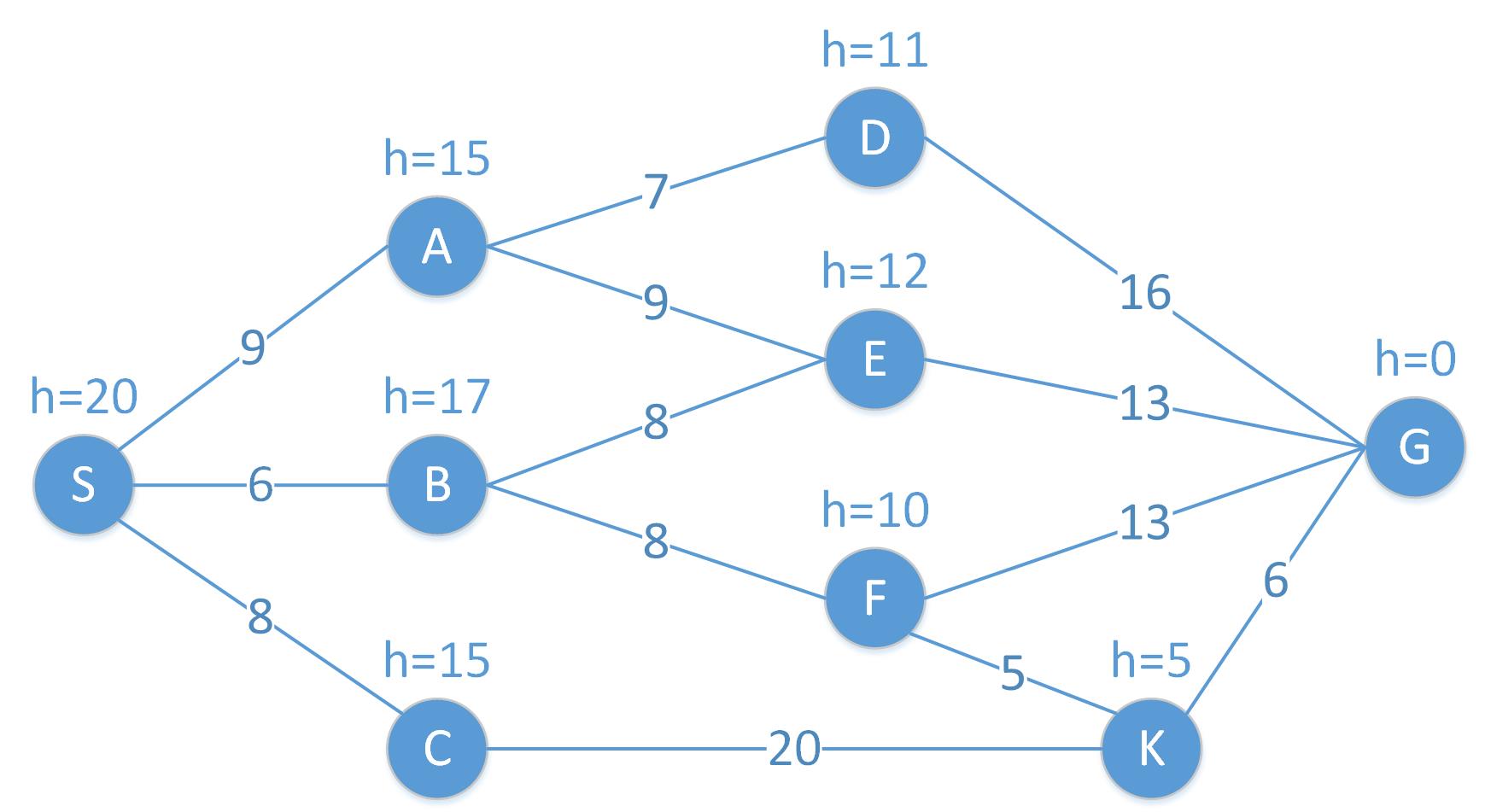
如下图所示，S为起始（start）节点，G为目标（goal）节点。

• 节点之间连线是两点的路径长度，如A到E的路径长度c(A,E) = 9。
• 节点旁的h值时当前节点到达目标节点（G）的预估值，如h(A)=15, 表示从当前点A到达目标点G的估计路径长度为15，此处h(x)即为启发函数，启发函数的设计有很多方法，具体可参考链接，此处不再扩展。
• 从起点S到达当前节点x的路径长度表示为g(x) 。
• 从起点S到达目标G并经过点x的估计距离长度表示为f(x) = g(x) + h(x)，该公式是A*算法的核心公式。
• A*算法通过不断的选择估计距离f最小的节点，逐渐构建最短路径。

逻辑流程

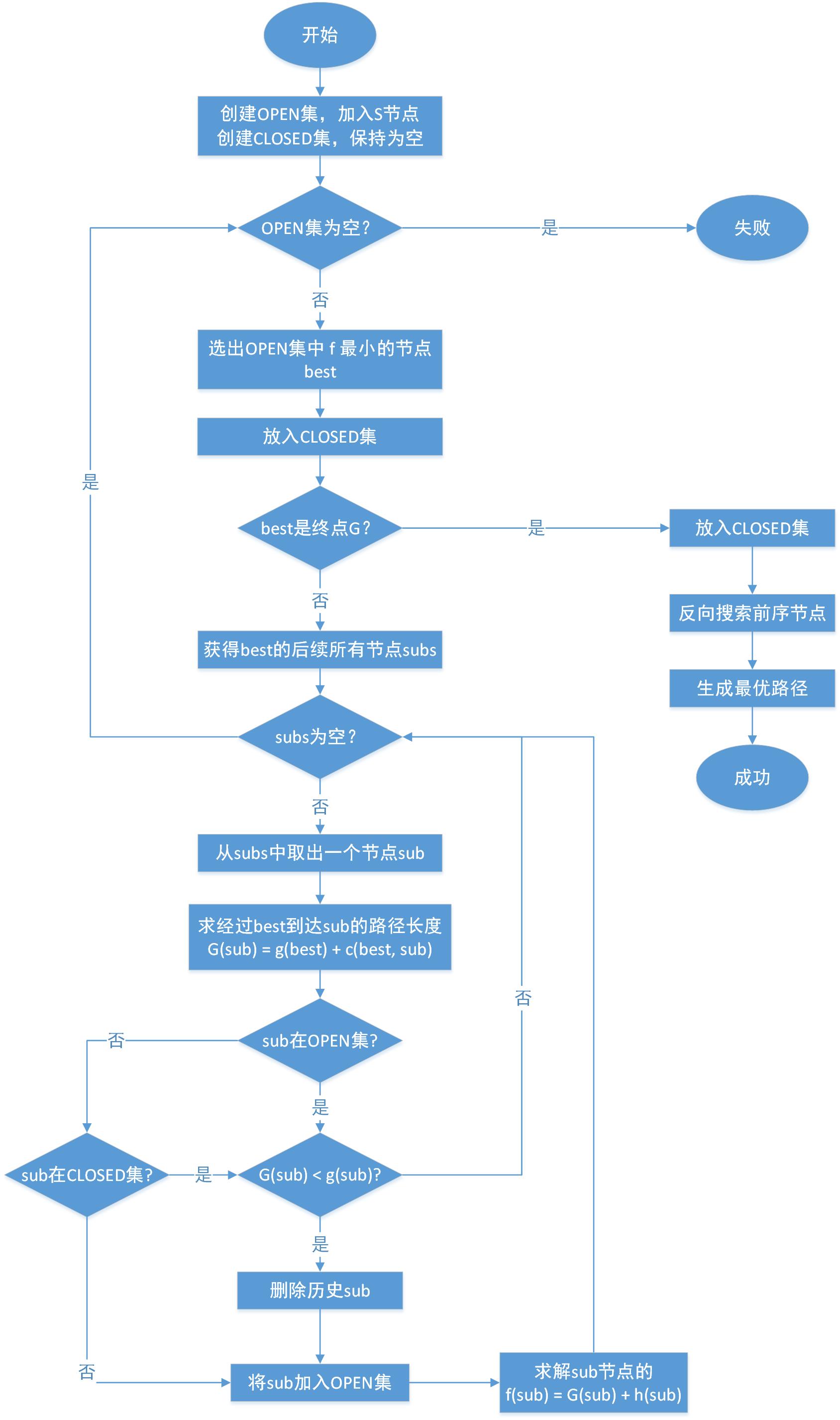
创建两个集合OPEN集，CLOSED集，算法核心是从OPEN集中选择最优（f值小最优，或f相同时，h小的更优）的节点到CLOSED集中，然后将其后继节点放入OPEN集中，然后重复操作选取最优节点，直到到达目标，或者OPEN为空为止。最后再CLOSED集中根据目标G所包含的前序节点逆序查找最后到达起点S，这个链路的逆序即最优路径，具体流程如下图。

 

搜索过程

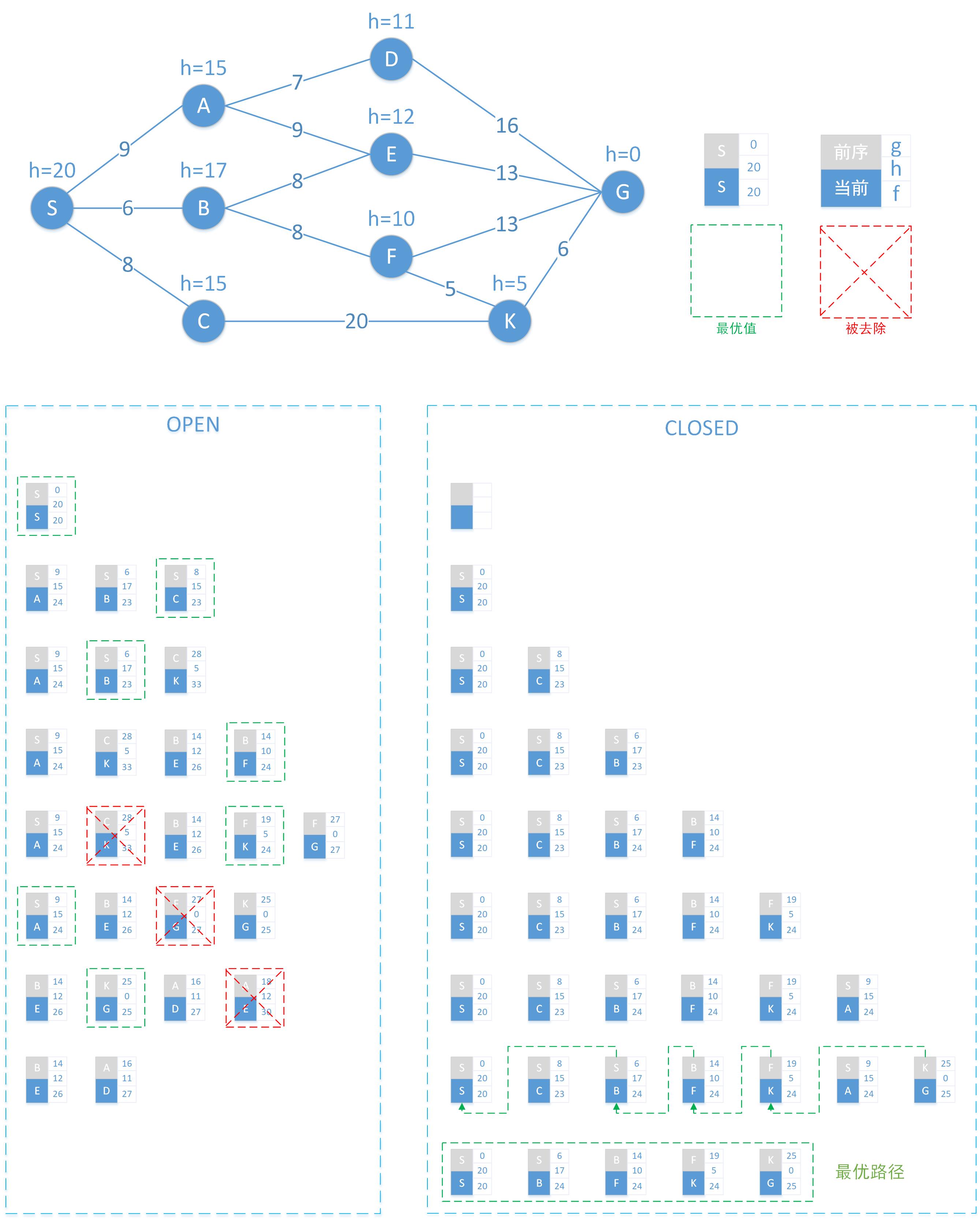
以下是前面网络的搜索过程展开图。

组合块中：

• 灰色为前序节点
• 蓝色当前节点x
• g：起点S到当前节点x的路径距离。
• h：当前节点x到终点G的估计距离
• f：起点S途径x到达终点G的估计距离，即 f = g + h
• 绿色框为当前OPEN集合中的最优节点
• 红色框表示当前OPEN集合中需要被删除的节点

在OPEN、CLOSED中每一行表示一次完整迭代完成时两集合中的节点集合。

最后的最优路径是：S->B->F->k->G

注：当两个节点f相同时，h小的更优

 

%**************************************************************************



disp('  Generating Grid ... ');
co=or;
crn=s;

noOfNodes  = nooc*noor;
nodmat=ones(nooc,noor,3);
nodmat(1:noOfNodes)=1:noOfNodes;
nodmat(:,:,2)=(find(nodmat(:,2,2)==1))*ones(1,noor);
nodmat(:,:,3)=ones(nooc,1)*(find(nodmat(2,:,3)==1));
nodmat(:,:,1)=flipdim((nodmat(:,:,1)),2);
nodmat(:,:,2)=flipdim((nodmat(:,:,2)),2);
nodmat(:,:,3)=flipdim((nodmat(:,:,3)),2);
noddata=reshape(nodmat,noOfNodes,3);


%rand('state', 0);

if plot_flag==1
    scrsz = get(0,'ScreenSize');
    h=figure(gcf);
    set(h,'Position',[scrsz(3)/8 scrsz(4)/8 scrsz(3)-2*scrsz(3)/8 ...
        scrsz(4)-2*scrsz(4)/8]);
    clf;
    hold on;
end


Astar_coor=noddata(:,2:3)*GTS;


netXloc = Astar_coor(:,1)';
netYloc = Astar_coor(:,2)';
axis([min(netXloc)-20  max(netXloc)+30  min(netYloc)-20  max(netYloc)+30])
Astar_connect = zeros(noOfNodes, noOfNodes);
Astar_coord = zeros(noOfNodes, 2);
for i = 1:noOfNodes
    
    Astar_coord(i,1) = netXloc(i);
    Astar_coord(i,2) = netYloc(i);
    
    for j = 1:noOfNodes
        distance = sqrt((netXloc(i) - netXloc(j))^2 + (netYloc(i) - netYloc(j))^2);
        ll=isempty(find(o==i, 1));
        lm=isempty(find(o==j, 1));
        if (distance <= R && ll==1 && lm==1)
            matrix(i, j) = distance;   % if set to '1', Dijkstra computes Spath in terms of hops; if set to 'distance', it is the real shortest path
            if i~=j % must be satisfied
                Astar_connect(i, j) = 1;
            else
                Astar_connect(i, j) = 0;
            end
            if plot_flag==1
                line([netXloc(i) netXloc(j)], [netYloc(i) netYloc(j)], 'color',[.65 .65 .65],'LineStyle', ':');
            end
        else
            matrix(i, j) = inf;
            Astar_connect(i, j) = 0;
        end;
    end;
end
for i = 1:noOfNodes
    if plot_nodenum
        text(netXloc(i)+20, netYloc(i), num2str(i));
    end
    if plot_flag==1
        
        if i==s
            plot(netXloc(i), netYloc(i),'square','MarkerSize',12,'MarkerFaceColor','g');
            hold on;
            
        end
        if i==d
            plot(netXloc(i), netYloc(i),'square','MarkerSize',12,'MarkerFaceColor','r');
        end
        
        if isempty(find(o==i))
            plot(netXloc(i), netYloc(i),'.');
        end
        
        
    end
end;


% activeNodes = [];
% for i = 1:noOfNodes,
%     % initialize the farthest node to be itself;
%     farthestPreviousHop(i) = i;     % used to compute the RTS/CTS range;
%     farthestNextHop(i) = i;
% end;

Astar_coord=Astar_coord';
%Astar_connect;
%%
disp('Generating Paths ... ')
%[path, totalCost, farthestPreviousHop, farthestNextHop] = dijkstra(noOfNodes, matrix, s, d, farthestPreviousHop, farthestNextHop);
% combo = [noOfNodes s-1 d-1 R/2];
%[Astar_path, Astar_search] = Astar(Astar_coord', Astar_connect, combo); % notice, we must put Astar_coord' rather than Astar_coord
%[Astar_paths,cost_astar,astar_time] = Astarm(Astar_coord, Astar_connect, s , d);
%[Astar_path,Astar_search]=Astar(Astar_coord, Astar_connect, combo);
[Astar_path,cost_astar,astar_time,Astar_dist] =komegaA(Astar_coord, Astar_connect, s, d, 1, inf, 0);
[komega_path,cost_komega,ko_time,komega_dist]=komegaA(Astar_coord, Astar_connect, s, d, k , b, n);
%%
if disp_summary==1
    Astar_path, komega_path,cost_astar,cost_komega,astar_time,ko_time, Astar_dist, komega_dist
end

if ~isempty(Astar_path)
    for i = 1:(length(Astar_path)-1)
        if plot_flag==1
            astr=line([netXloc(Astar_path(i)) netXloc(Astar_path(i+1))], [netYloc(Astar_path(i)) netYloc(Astar_path(i+1))], 'Color','r','LineWidth', 2, 'LineStyle', '-.');
            if plot_nodenum==1
                text(netXloc(i), netYloc(i), num2str(i));
            end
        end
    end;
end;
if ~isempty(komega_path)
    for i = 1:(length(komega_path)-1)
        if plot_flag==1
            kom=line([netXloc(komega_path(i)) netXloc(komega_path(i+1))], [netYloc(komega_path(i)) netYloc(komega_path(i+1))], 'Color','g','LineWidth', 2, 'LineStyle', '-');
            if plot_nodenum==1
                text(netXloc(i), netYloc(i), num2str(i));
            end
        end
    end;
end;

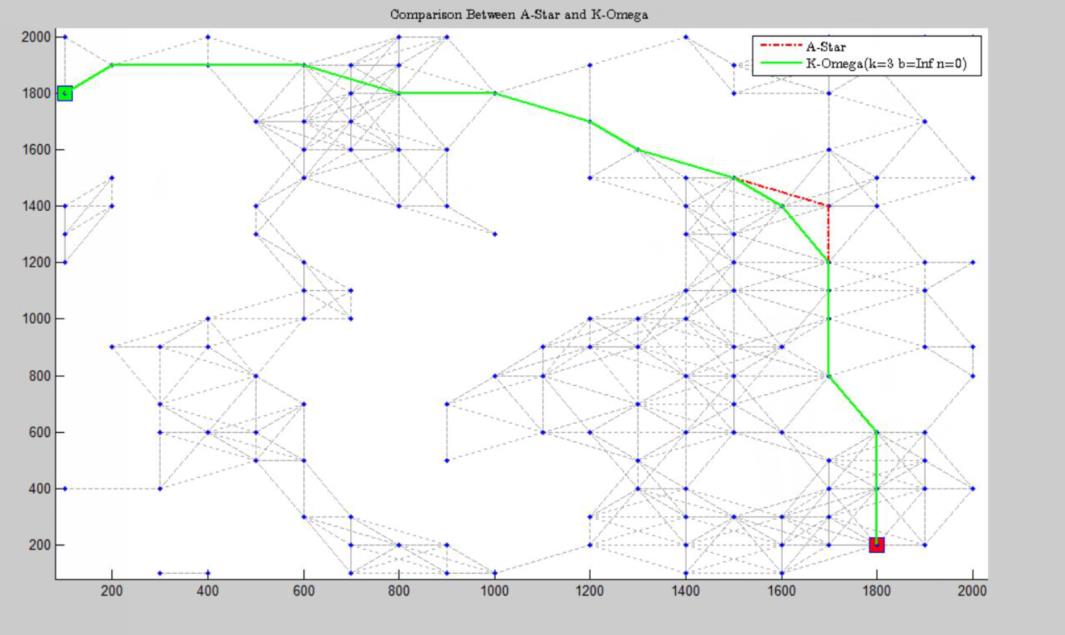
rest=title('Comparison Between A-Star and K-Omega');
set(rest,'Interpreter','latex');
dkstr=strcat('K-Omega(k=',num2str(k),' b=',num2str(b),' n=',num2str(n),')');
kleg=legend([astr kom],'A-Star',dkstr);hold on;
set(kleg,'Interpreter','latex');



if plot_flag == 1
    hold off;
end

% Execute if K-Omega has not yet executed harware
if (n==0)
    [done]=execnxt(komega_path);
end

% If Analysis mode requested, perform analysis
if AnalysisMode==1
    AnalyzeKO;
end

​

完整代码或仿真咨询QQ1575304183