SVR预测基于混沌灰狼优化支持向量机回归预测SVR模型matlab源码

Posted 2021-06-11 Matlab咨询QQ1575304183

一、简介

1.1 支持向量机

1、支持向量机（ SVM ）是一种比较好的实现了结构风险最小化思想的方法。它的机器学习策略是结构风险最小化原则 为了最小化期望风险，应同时最小化经验风险和置信范围）

支持向量机方法的基本思想：

（ 1 ）它是专门针对有限样本情况的学习机器，实现的是结构风险最小化：在对给定的数据逼近的精度与逼近函数的复杂性之间寻求折衷，以期获得最好的推广能力；

（ 2 ）它最终解决的是一个凸二次规划问题，从理论上说，得到的将是全局最优解，解决了在神经网络方法中无法避免的局部极值问题；

（ 3 ）它将实际问题通过非线性变换转换到高维的特征空间，在高维空间中构造线性决策函数来实现原空间中的非线性决策函数，巧妙地解决了维数问题，并保证了有较好的推广能力，而且算法复杂度与样本维数无关。

目前， SVM 算法在模式识别、回归估计、概率密度函数估计等方面都有应用，且算法在效率与精度上已经超过传统的学习算法或与之不相上下。  

       对于经验风险R，可以采用不同的损失函数来描述，如e不敏感函数、Quadratic函数、Huber函数、Laplace函数等。

      核函数一般有多项式核、高斯径向基核、指数径向基核、多隐层感知核、傅立叶级数核、样条核、 B 样条核等，虽然一些实验表明在分类中不同的核函数能够产生几乎同样的结果，但在回归中，不同的核函数往往对拟合结果有较大的影响

2、支持向量回归算法

主要是通过升维后，在高维空间中构造线性决策函数来实现线性回归，用e不敏感函数时，其基础主要是 e 不敏感函数和核函数算法。

若将拟合的数学模型表达多维空间的某一曲线，则根据e 不敏感函数所得的结果，就是包括该曲线和训练点的“ e管道”。在所有样本点中，只有分布在“管壁”上的那一部分样本点决定管道的位置。这一部分训练样本称为“支持向量”。为适应训练样本集的非线性，传统的 拟合方法通常是在线性方程后面加高阶项。此法诚然有效，但由此增加的可调参数未免增加了过拟合的风险。支持向量回归算法采用核函数解决这一矛盾。用核函数 代替线性方程中的线性项可以使原来的线性算法“非线性化”，即能做非线性回归。与此同时，引进核函数达到了“升维”的目的，而增加的可调参数是过拟合依然 能控制。

1.2 灰狼算法

灰狼优化算法（Grey Wolf Optimizer，GWO）由澳大利亚格里菲斯大学学者 Mirjalili 等人于2014年提出来的一种群智能优化算法。该算法受到了灰狼捕食猎物活动的启发而开发的一种优化搜索方法，它具有较强的收敛性能、参数少、易实现等特点。近年来受到了学者的广泛关注，它己被成功地应用到了车间调度、参数优化、图像分类等领域中。

---

算法原理：

灰狼隶属于群居生活的犬科动物，且处于食物链的顶层。灰狼严格遵守着一个社会支配等级关系。如图：

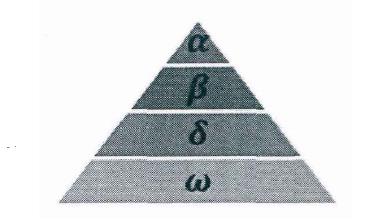
社会等级第一层：狼群中的头狼记为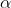 

社会等级第二层：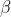

社会等级第三层：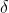

社会等级第四层：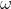

GWO 优化过程包含了灰狼的社会等级分层、跟踪、包围和攻击猎物等步骤，其步骤具体情况如下所示。

１）社会等级分层（Social Hierarchy）当设计 GWO 时，首先需构建灰狼社会等级层次模型。计算种群每个个体的适应度，将狼群中适应度最好的三匹灰狼依次标记为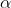 

２）包围猎物（ Encircling Prey ）灰狼捜索猎物时会逐渐地接近猎物并包围它，该行为的数学模型如下：

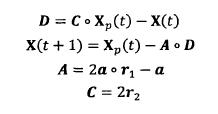
式中：t 为当前迭代次数：。表示 hadamard 乘积操作；A 和 C 是协同系数向量；Xp 表示猎物的位置向量； X(t) 表示当前灰狼的位置向量；在整个迭代过程中 a 由2 线性降到 0； r1 和 r2 是 [0，1] 中的随机向量。

３）狩猎（ Hunring）

灰狼具有识别潜在猎物（最优解）位置的能力，搜索过程主要靠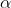 

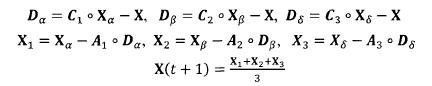
式中：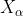

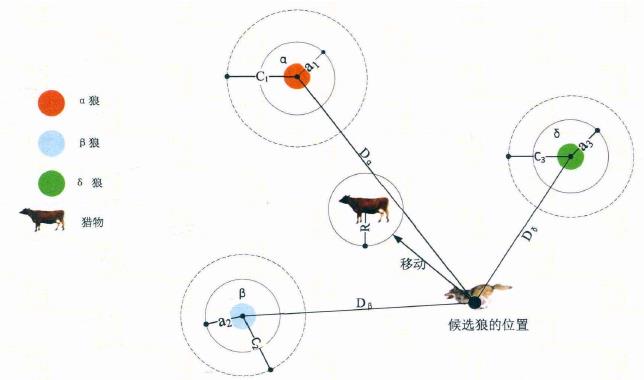
从图中可看出，候选解的位置最终落在被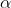 

４）攻击猎物（Attacking Prey）构建攻击猎物模型的过程中，根据2)中的公式，ａ值的减少会引起 A 的值也随之波动。换句话说，A 是一个在区间［-a，a］（备注：原作者的第一篇论文里这里是[-2a,2a]，后面论文里纠正为[-a,a]）上的随机向量，其中ａ在迭代过程中呈线性下降。当 A 在［-1，１］区间上时，则捜索代理（Search Agent）的下一时刻位置可以在当前灰狼与猎物之间的任何位置上。

５）寻找猎物（Search for Prey）灰狼主要依赖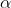 

二、源代码

tic % 计时
%% 清空环境导入数据
clear
clc
close all
format long
load wndspd
%% HGWO-SVR
% 训练/测试数据准备
x=wndspd;
embed=6;        % 用多少个来预测
test_size=12;   % 预测多少个数据
[input_train,output_train,input_test,output_test]=transfer(x,embed,1,1,1,length(x)-test_size);
input_train=input_train'; % 训练集输入 m行n列，m表示样本个数，n表示每次用多少个预测下1个
output_train=output_train'; % 训练集输出 m行1列
input_test=input_test'; % 测试集输入   p行n列，p表示预测多少个数据
output_test=output_test'; % 测试集输出 p行1列
para=[20,20,0.2,0.8,0.2];
% 分别表示：种群规模、最大迭代次数、缩放因子下界、缩放因子上界、交叉概率
[bestc,bestg,test_pre]=my_HGWO_SVR(para,input_train,output_train,input_test,output_test);

%% 打印参数选择结果
disp('打印选择结果');
str=sprintf('Best bestc = %g，Best bestg = %g',bestc,bestg);
disp(str)

%% 画图
err_pre=x(end-test_size+1:end)-test_pre;
figure('Name','测试数据残差图')
set(gcf,'unit','centimeters','position',[0.5,5,30,5])
plot(err_pre,'*-');
figure('Name','原始-预测图')
plot(test_pre,'*r-');hold on;plot(x(end-test_size+1:end),'bo-');
legend('预测','原始')
set(gcf,'unit','centimeters','position',[0.5,13,30,5])

%% 预测性能计算
result=[x(end-test_size+1:end),test_pre];
MAE=mymae(result(:,1),result(:,2));
MAPE=mymape(result(:,1),result(:,2));
MSE=mymse(result(:,1),result(:,2));

%% 显示程序运行时间
toc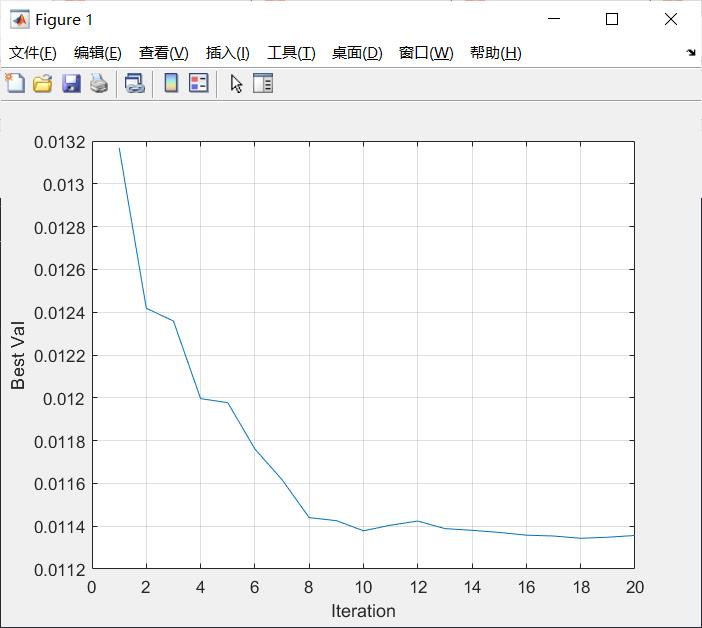

​

完整代码或者仿真咨询添加QQ1575304183