SVM预测基于SVM和LSR交通流预测matlab源码

Posted 2021-06-11 Matlab咨询QQ1575304183

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了SVM预测基于SVM和LSR交通流预测matlab源码相关的知识，希望对你有一定的参考价值。

支持向量机（support vector machines, SVM）是二分类算法，所谓二分类即把具有多个特性（属性）的数据分为两类，目前主流机器学习算法中，神经网络等其他机器学习模型已经能很好完成二分类、多分类，学习和研究SVM，理解SVM背后丰富算法知识，对以后研究其他算法大有裨益；在实现SVM过程中，会综合利用之前介绍的一维搜索、KKT条件、惩罚函数等相关知识。本篇首先通过详解SVM原理，后介绍如何利用python从零实现SVM算法。

为便于理解，假设样本有两个属性，可以把属性值分别对应到二维空间轴的x,y轴上，如下图所示：

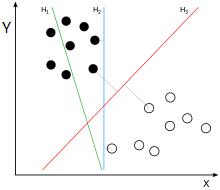
二维坐标.png

实例中样本明显的分为两类，黑色实心点不妨为类别一，空心圆点可命名为类别二，在实际应用中会把类别数值化，比如类别一用1表示，类别二用-1表示，称数值化后的类别为标签。每个类别分别对应于标签1、还是-1表示没有硬性规定，可以根据自己喜好即可，需要注意的是，由于SVM算法标签也会参与数学运算，这里不能把类别标签设为0。

还是对应于上图，如果能需要找到一条直线，将上述的实心点与空心点分为两个部分，当下次还有其他样本点时，将其属性值作为坐标绘制到坐标轴上后，根据新样本点与直线位置关系，就可以判断出其类别。满足这样直线有无数条，SVM是要找到最合适一条：观察上图，绿线肯定不行，该条分类直线在没有验证集前提下已经错了；而蓝色线和红色都可以实现分类，蓝色线与实心黑点靠的太近，相比而言，红色线更‘公允’些。红色线就是SVM需要找出的分类直线，数学语言描述红线的‘公允’特性可表述为：将黑点和空心点视为两个集合，如果找到一个直线，使得黑点集合中的一些点离直线最近，这些点到该直线距离为d;空心点集合中也能找到一系列的点，离直线最近，距离同样也是d,则该直线就是我们要找到线性分类器，同时称两个集合中离直线最近的点为支持向量，SVM支持向量机就是由此得名的。

一些算法书籍中这样描述SVM算法，找出一个直线，使得直线与两边集合最近的点的间隔空间最大，从上图也可以看出来，黑色点离蓝线最近的点，其距离小于到红线距离（直角的斜边）。能找到支持向量就一定找到分类直线，反之亦然，以上是针对两个属性值，通过观察二维平面即可以引出SVM的算法的特点，如果样本属性非常多呢，如何归纳算法的规律性？首先说下凸集可分离定理，该定理不仅是SVM的核心理论支持，更是机器学习算法的基石。

一、凸集可分离定理

还是以二维空间为例，中学时代我们就学过直线方程，比如有直线方程y=2x-1,如下图所示：

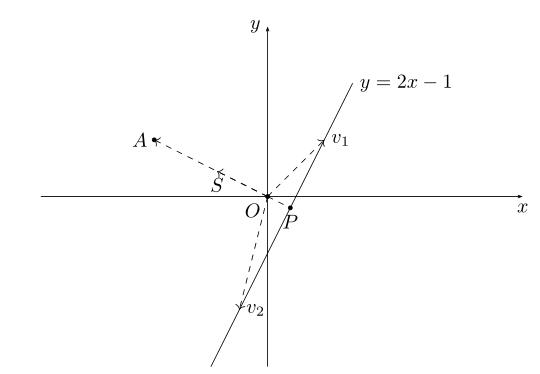
超平面.png

把直线方程y=2x-1写成内积形式:

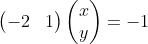
内积一.gif

向量(-2,1)对应上图中OA向量，把OA向量变为单位向量，即方向与OA相同，模为1向量OS,S的坐标为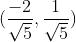坐标1.gif ,将直线方程两边同除以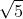，可得：

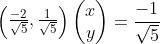
内积而.gif

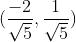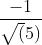(x,y)代表直线y=2x-1上任意一点，上式说明y=2x-1上任意一点与单位向量S: 坐标1.gif 的内积是标准内积1.gif ，图中向量OP的长度为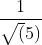标准内积3.gif ，取负号是因为OP向量方向与OS方向相反；上图中向量v1、v2在OS向量上投影都是OP，这个例子说明：通过引入一个向量OS，直线y=2x-1上无数的点在向量OS上都可以用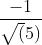来表示,或者说，直线y=2x-1在向量OS上都可以用坐标(0, 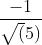标准内积1.gif )表示。通过内积投影的方式，可以把高维数据变为向量上一个实数，这是一个线性泛函的过程，数学领域中常用内积来降低数据维度，把多维数据处理成一个实数便于后期分析、处理。

引申到任意维度时，上面方程可用集合公式表达：S:{x | pTx=α} x∈Rn。对应于上图：p向量对应向量OS,x为直线上任意一点，在SVM算法中，称x点构成的集合S为超平面。有时高维数据集合投影到向量p的内积值是一个范围：比如{x | pTx>=α}或{y | pTy<=-α},高维数据被投影到向量p的两个区间上：

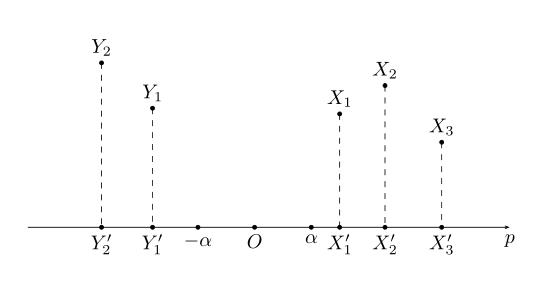
凸集.png

接下来介绍凸集分离定理：

上图中X，Y在高维空间中都是凸集，且X∩Y=Φ;将X、Y投影到向量p上后，可以得到两个凸集X'，Y',在向量p上X'、Y'一定处在向量p的两端，即X'，Y'两个凸集是可分离的。

注意定理中有两个条件，一是X，Y是凸集，二是X，Y交集为空集。X'，Y'可分离意味着在向量p上可以将两者区分开，而X与X'、Y与Y'都是一一映射，X'，Y'可区分开就间接地意味着X，Y也可区分开，这里所谓的'可区分开'也就是SVM所要实现的二分法。凸集可分离定理说明两个没有交集的凸集是线性可分的，同时，如果两个数据集不能线性分开时，可以通过核函数将数据变为两个凸集，所以凸集可分离定理对核函数生成也有着指导意义。

二、 SVM算法

2.1 超平面与最大间隔

前面介绍过，能把数据实现二分类的线性分类器称为超平面，SVM算法需要求出最大间隔的超平面，可设超平面为S:{x|pTx=α},由于pTx=α等式两边可除以一个正数就可以把p归一化为单位向量，不妨设p是一个已经处理后的单位向量，此设定不影响SVM算法。一般文献中，超平面通常写成隐函数形式:

S:{x|pTx-α=0} x∈Rn，p∈Rn，||p||=1

由几何知识可知，空间任意一点x到超平面S的距离公式为：

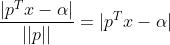
距离公式.gif

属于两个分类的支持向量到该超平面的距离都为d , d>0,由于支持向量是各自分类数据中，距离超平面最近的点，针对所有数据有以下不等式：

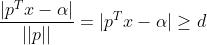条件.gif ⑴

公式(1)两边同除以d,可得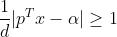：处理1.gif ,使用换元法，令：

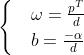设定2.gif ⑵

这样就得到约束条件常见形式:

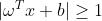条件3.gif ⑶

接下来要把公式(3)脱掉绝对值符号，SVM是一个二分类问题:可设定ωTx+b>=1时分类标签y=1;ωTx+b<=-1时分类标签y=-1,这样一来,所有的数据都有不等式：

y(ωTx+b)>=1 ④

再回过头来看换元设定，ω=pT/d,等式两边取范数运算有：||ω||=||pT||/d=1/d,可得d=1/||ω||,SVM算法需要在满足公式4约束的基础上，使得间隔距离d最大。假设待分类数据共有m个，实现SVM算法等同于求解一个带有不等式约束的非线性规划问题：

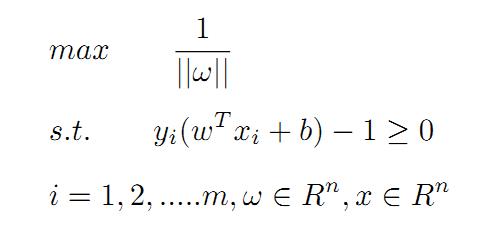
svm线性规划.png

上面的问题也可以表述为求最小值的问题：

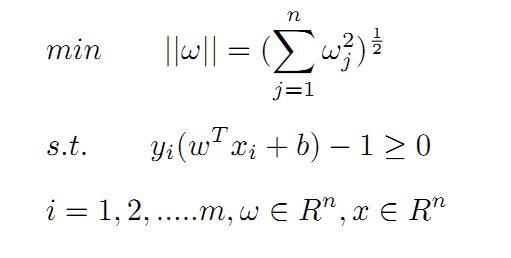svm线性规划22.png ⑤

超平面实现分类效果、以及各个参数之间关系可参考下图：

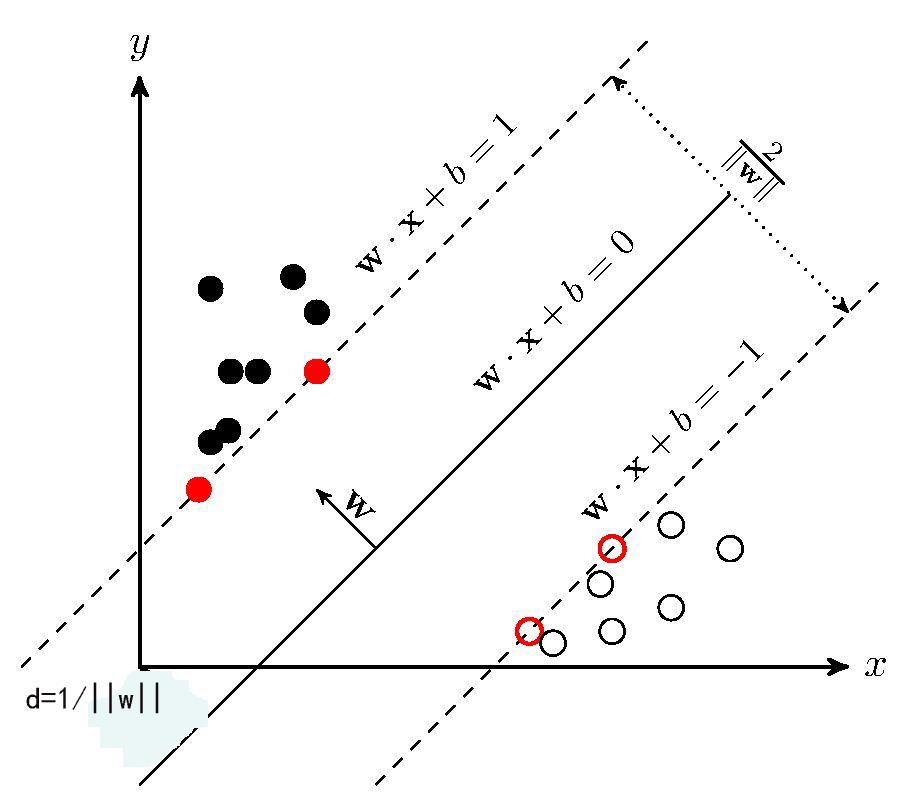
2.2 最大软间隔

实践中由于异常数据的存在，导致超平面不能完全将数据分为两部分，如下图：

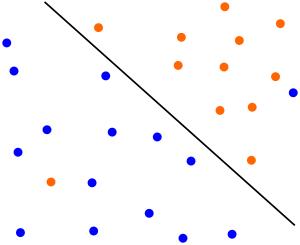
软间隔1.png

两个分类中混杂了少量的异常数据，除去极少数的异常点，上图中超平面能分离大多数样本。⑤式引入松弛变量后可以兼容上图的情形：

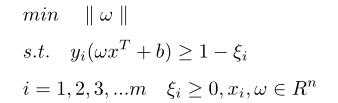松弛变量.png （5.1）

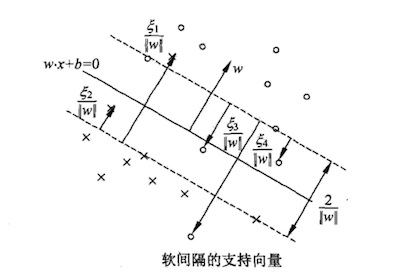
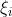正常情况下等于0，表示样本点分列在支持向量的两侧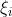；>0时代表的是异常数据：当0<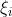<1时，代表数据在超平面与支持向量之间，如上图中的点2和点4；而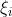>1时代表数据到了对方空间中，如上图的点1和点3。满足(5.1)式的间隔称为软间隔，软间隔优化结果不仅需要支持向量的间隔最大，还要使得各个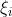尽量的小。换句话说，超平面确定后，被定义为异常数据的样本个数要尽量的少。

[x_train, y_train, x_test, y_test]= data(); % load data


% Project part 1

disp('--------Project part 1----------');

plot_alldata(x_train, y_train, x_test, y_test); % plot all data

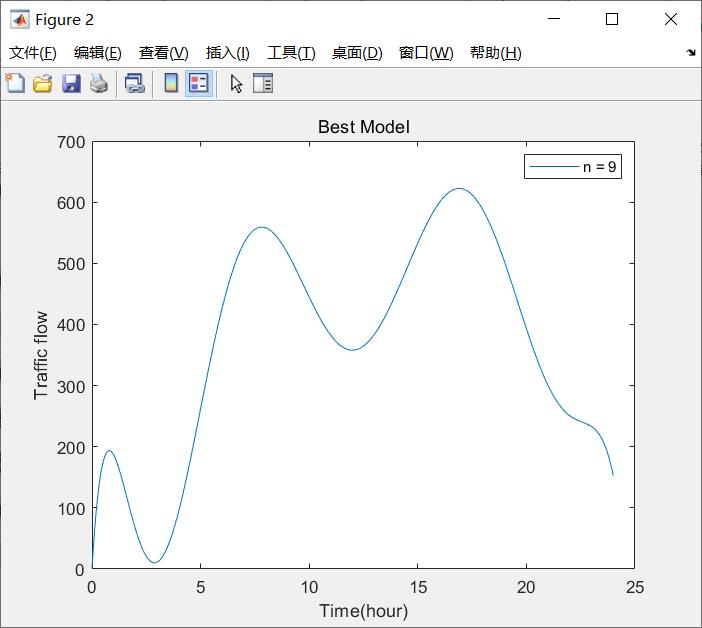
fit_data(x_train, y_train, x_test, y_test); % fitting data & plot the best model


% Project part 2

disp('--------Project part 2----------');

svm(x_train,y_train,x_test,y_test); % svm model fitting & plots

结果展示

>> main_project

警告: 在为表创建变量名称之前，对文件中的列标题进行了修改，以使其成为有效的 MATLAB 标识符。原始列标题保存在 VariableDescriptions 属性

中。

将 'PreserveVariableNames' 设置为 true 以使用原始列标题作为表变量名称。

--------Project part 1----------

For n =

1


mse_train=

2.9834e+04


r2_train=

0.1084


mse_test=

3.2158e+04


r2_test=

0.1305


---------------

For n =

2


mse_train=

1.3195e+04


r2_train=

0.6057


mse_test=

1.5085e+04


r2_test=

0.6028


---------------

For n =

3


mse_train=

1.2732e+04


r2_train=

0.6195


mse_test=

1.4313e+04


r2_test=

0.6237


---------------

For n =

4


mse_train=

1.2687e+04


r2_train=

0.6208


mse_test=

1.4152e+04


r2_test=

0.6283


---------------

For n =

5


mse_train=

1.1969e+04


r2_train=

0.6423


mse_test=

1.3453e+04


r2_test=

0.6470


---------------

For n =

6


mse_train=

6.3150e+03


r2_train=

0.8113


mse_test=

6.8526e+03


r2_test=

0.8285


---------------

For n =

7


警告: 多项式未正确设置条件。请添加具有不同 X 值的点，减少多项式的次数，或者尝试按照 HELP POLYFIT 中所述进行中心化和缩放。

> In polyfit (line 79)

In fit_data (line 5)

In main_project (line 6)

mse_train=

6.2697e+03


r2_train=

0.8126


mse_test=

6.8162e+03


r2_test=

0.8296


---------------

For n =

8


警告: 多项式未正确设置条件。请添加具有不同 X 值的点，减少多项式的次数，或者尝试按照 HELP POLYFIT 中所述进行中心化和缩放。

> In polyfit (line 79)

In fit_data (line 5)

In main_project (line 6)

mse_train=

3.0802e+03


r2_train=

0.9079


mse_test=

3.3461e+03


r2_test=

0.9258


---------------

For n =

9


警告: 多项式未正确设置条件。请添加具有不同 X 值的点，减少多项式的次数，或者尝试按照 HELP POLYFIT 中所述进行中心化和缩放。

> In polyfit (line 79)

In fit_data (line 5)

In main_project (line 6)

mse_train=

2.9532e+03


r2_train=

0.9117


mse_test=

3.3297e+03


r2_test=

0.9261


---------------

警告: 多项式未正确设置条件。请添加具有不同 X 值的点，减少多项式的次数，或者尝试按照 HELP POLYFIT 中所述进行中心化和缩放。

> In polyfit (line 79)

In fit_data (line 32)

In main_project (line 6)

model coefficient:

0.0000 -0.0001 0.0074 -0.2230 3.8894 -39.3375 219.0309 -587.1015 589.8787 0.1253


--------Project part 2----------

-------Gaussian-------

CASE1 - default:

mse =

1.4268e+03


r2 =

0.9771


CASE2:

mse =

1.6445e+03


r2 =

0.9758


CASE3:

mse =

1.4664e+03


r2 =

0.9772


OPTIMIZED:

|====================================================================================================================|

| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Epsilon |

| | result | log(1+loss) | runtime | (observed) | (estim.) | | | |

|====================================================================================================================|

| 1 | Best | 10.431 | 0.89758 | 10.431 | 10.431 | 394.32 | 736.91 | 10.115 |

| 2 | Accept | 10.437 | 0.1401 | 10.431 | 10.432 | 0.0011055 | 0.053194 | 47.555 |

| 3 | Best | 10.426 | 0.071798 | 10.426 | 10.426 | 25.627 | 30.172 | 19150 |

| 4 | Accept | 10.426 | 0.054275 | 10.426 | 10.426 | 1.1377 | 0.0012314 | 14020 |

| 5 | Accept | 10.428 | 0.14271 | 10.426 | 10.426 | 470.09 | 836.88 | 0.41086 |

| 6 | Accept | 10.426 | 0.037576 | 10.426 | 10.426 | 2.6562 | 0.0010627 | 3310.4 |

| 7 | Accept | 10.426 | 0.034094 | 10.426 | 10.426 | 0.0010521 | 24.307 | 5816.8 |

| 8 | Best | 10.074 | 0.065287 | 10.074 | 10.074 | 17.708 | 0.056046 | 1.6934 |

| 9 | Accept | 10.426 | 0.038535 | 10.074 | 10.074 | 132.62 | 0.08944 | 3956.1 |

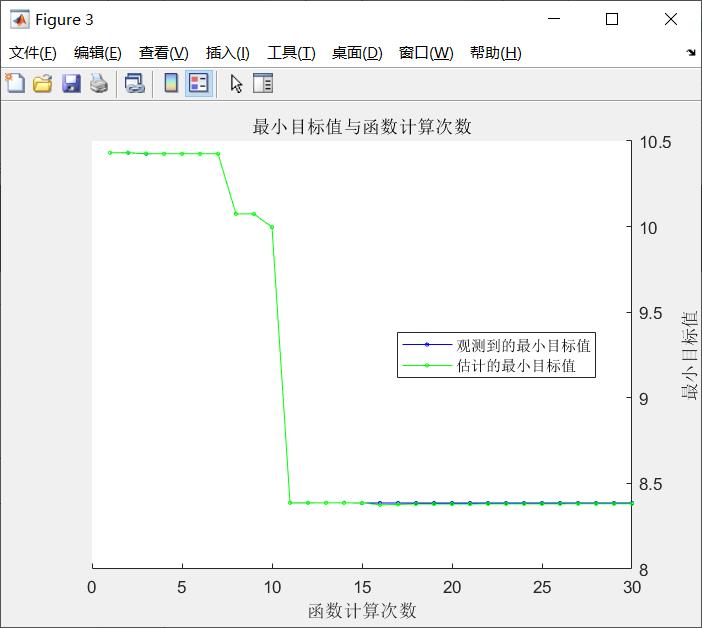
| 10 | Best | 9.9965 | 0.06095 | 9.9965 | 9.9965 | 21.302 | 0.036971 | 0.28347 |

| 11 | Best | 8.3865 | 0.07324 | 8.3865 | 8.3867 | 642.83 | 0.0044812 | 0.22288 |

| 12 | Accept | 9.5704 | 0.046863 | 8.3865 | 8.3867 | 993.59 | 0.0028159 | 156.21 |

| 13 | Best | 8.3864 | 0.071449 | 8.3864 | 8.3864 | 975.49 | 0.0012285 | 0.27834 |

| 14 | Accept | 8.3865 | 0.064198 | 8.3864 | 8.3862 | 507.99 | 0.0010299 | 0.24398 |

| 15 | Best | 8.3853 | 0.06352 | 8.3853 | 8.386 | 611.28 | 0.0019797 | 0.51237 |

| 16 | Accept | 8.3865 | 0.069143 | 8.3853 | 8.3751 | 660.76 | 0.0013634 | 0.22497 |

| 17 | Accept | 8.386 | 0.068376 | 8.3853 | 8.3773 | 828.03 | 0.0024918 | 0.35096 |

| 18 | Accept | 8.3861 | 0.067393 | 8.3853 | 8.3799 | 732.96 | 0.0014109 | 0.32464 |

| 19 | Accept | 8.3861 | 0.062025 | 8.3853 | 8.3797 | 520.66 | 0.0022738 | 0.30965 |

| 20 | Accept | 8.3863 | 0.066882 | 8.3853 | 8.3797 | 668.85 | 0.0018481 | 0.24784 |

|====================================================================================================================|

| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Epsilon |

| | result | log(1+loss) | runtime | (observed) | (estim.) | | | |

|====================================================================================================================|

| 21 | Accept | 8.3866 | 0.063036 | 8.3853 | 8.3796 | 903.96 | 0.0023935 | 0.22712 |

| 22 | Accept | 8.3864 | 0.065384 | 8.3853 | 8.3807 | 988.43 | 0.0056305 | 0.26435 |

| 23 | Accept | 8.3857 | 0.080765 | 8.3853 | 8.3808 | 768.95 | 0.0028004 | 0.40427 |

| 24 | Accept | 10.434 | 0.047994 | 8.3853 | 8.3807 | 0.036485 | 962.56 | 0.22485 |

| 25 | Accept | 10.432 | 0.091279 | 8.3853 | 8.3805 | 0.065077 | 0.001002 | 0.22826 |

| 26 | Accept | 10.426 | 0.03629 | 8.3853 | 8.3804 | 0.15322 | 962.81 | 20662 |

| 27 | Accept | 8.3865 | 0.063816 | 8.3853 | 8.3815 | 648.08 | 0.0022537 | 0.24789 |

| 28 | Accept | 10.426 | 0.035603 | 8.3853 | 8.3814 | 0.0013648 | 0.0010192 | 21509 |

| 29 | Accept | 10.434 | 0.048371 | 8.3853 | 8.3813 | 0.0010406 | 767.16 | 0.32152 |

| 30 | Accept | 8.3866 | 0.079493 | 8.3853 | 8.3814 | 912.54 | 0.0035796 | 0.24067 |


__________________________________________________________

优化完成。

达到 MaxObjectiveEvaluations 30。

函数计算总次数: 30

总经过时间: 26.8651 秒。

总目标函数计算时间: 2.808


观测到的最佳可行点:

BoxConstraint KernelScale Epsilon

_____________ ___________ _______


611.28 0.0019797 0.51237


观测到的目标函数值 = 8.3853

估计的目标函数值 = 8.3814

函数计算时间 = 0.06352


估计的最佳可行点(根据模型):

BoxConstraint KernelScale Epsilon

_____________ ___________ _______


668.85 0.0018481 0.24784


估计的目标函数值 = 8.3814

估计的函数计算时间 = 0.067649


mse =

2.0132e+03


r2 =

0.9671


-------RBF-------

CASE1 - default:

mse =

1.4268e+03


r2 =

0.9771


CASE2:

mse =

1.4664e+03


r2 =

0.9772


CASE3:

mse =

1.4591e+03


r2 =

0.9766


OPTIMIZED:

|====================================================================================================================|

| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Epsilon |

| | result | log(1+loss) | runtime | (observed) | (estim.) | | | |

|====================================================================================================================|

| 1 | Best | 10.437 | 0.064096 | 10.437 | 10.437 | 0.0024199 | 0.012131 | 0.82686 |

| 2 | Best | 10.424 | 0.035964 | 10.424 | 10.425 | 792.75 | 0.51879 | 2798.3 |

| 3 | Accept | 10.424 | 0.033958 | 10.424 | 10.424 | 0.0015712 | 1.7285 | 12257 |

| 4 | Best | 10.315 | 0.052699 | 10.315 | 10.315 | 64.709 | 60.677 | 0.43676 |

| 5 | Accept | 10.43 | 0.053824 | 10.315 | 10.341 | 598.05 | 816.9 | 0.22621 |

| 6 | Best | 10.315 | 0.049229 | 10.315 | 10.315 | 65.348 | 60.686 | 0.73483 |

| 7 | Accept | 10.424 | 0.032769 | 10.315 | 10.315 | 0.068404 | 38.268 | 382.69 |

| 8 | Best | 10.23 | 0.046858 | 10.23 | 10.23 | 163.2 | 61.687 | 38.56 |

| 9 | Accept | 10.424 | 0.03518 | 10.23 | 10.23 | 4.1446 | 62.152 | 2623.5 |

| 10 | Accept | 10.424 | 0.033162 | 10.23 | 10.23 | 199.56 | 62.459 | 2073.2 |

| 11 | Best | 10.113 | 0.048122 | 10.113 | 10.113 | 307.74 | 60.662 | 18.094 |

| 12 | Accept | 10.44 | 0.052386 | 10.113 | 10.113 | 0.0020345 | 55.312 | 10.057 |

| 13 | Best | 9.5718 | 0.048005 | 9.5718 | 10.002 | 694.03 | 28.973 | 12.634 |

| 14 | Best | 7.8382 | 0.057983 | 7.8382 | 7.8399 | 932.32 | 4.265 | 11.006 |

| 15 | Accept | 10.433 | 0.041807 | 7.8382 | 7.8384 | 0.39209 | 4.3466 | 348.78 |

| 16 | Accept | 8.111 | 0.055765 | 7.8382 | 7.8388 | 976.56 | 5.5148 | 1.4862 |

| 17 | Accept | 10.424 | 0.032728 | 7.8382 | 7.8386 | 992.59 | 4.0578 | 2128.8 |

| 18 | Best | 7.65 | 0.066125 | 7.65 | 7.65 | 819.88 | 2.352 | 4.6514 |

| 19 | Accept | 7.7333 | 0.062206 | 7.65 | 7.6576 | 912.6 | 3.2069 | 4.5506 |

| 20 | Best | 7.6008 | 0.071054 | 7.6008 | 7.6011 | 990.85 | 1.656 | 8.9775 |

|====================================================================================================================|

| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Epsilon |

| | result | log(1+loss) | runtime | (observed) | (estim.) | | | |

|====================================================================================================================|

| 21 | Accept | 7.6387 | 0.098309 | 7.6008 | 7.6007 | 982.52 | 0.83259 | 2.7969 |

| 22 | Accept | 7.6275 | 0.076077 | 7.6008 | 7.6018 | 797.68 | 0.9112 | 0.29266 |

| 23 | Accept | 7.9363 | 0.0648 | 7.6008 | 7.6019 | 994.85 | 0.32932 | 0.23043 |

| 24 | Accept | 7.6935 | 0.045446 | 7.6008 | 7.6018 | 29.346 | 0.967 | 0.37377 |

| 25 | Accept | 7.6274 | 0.080696 | 7.6008 | 7.6017 | 910.2 | 0.9449 | 0.91925 |

| 26 | Accept | 7.6121 | 0.077758 | 7.6008 | 7.603 | 943 | 1.1589 | 5.0625 |

| 27 | Accept | 7.6153 | 0.062063 | 7.6008 | 7.6032 | 517.55 | 1.4588 | 0.25744 |

| 28 | Accept | 7.6051 | 0.058127 | 7.6008 | 7.6033 | 254.49 | 1.155 | 0.38512 |

| 29 | Accept | 7.6205 | 0.075103 | 7.6008 | 7.603 | 999.64 | 1.4418 | 1.9978 |

| 30 | Accept | 7.6088 | 0.051488 | 7.6008 | 7.604 | 227.74 | 1.2748 | 1.9489 |


__________________________________________________________

优化完成。

达到 MaxObjectiveEvaluations 30。

函数计算总次数: 30

总经过时间: 20.9975 秒。

总目标函数计算时间: 1.6638


观测到的最佳可行点:

BoxConstraint KernelScale Epsilon

_____________ ___________ _______


990.85 1.656 8.9775


观测到的目标函数值 = 7.6008

估计的目标函数值 = 7.604

函数计算时间 = 0.071054


估计的最佳可行点(根据模型):

BoxConstraint KernelScale Epsilon

_____________ ___________ _______


254.49 1.155 0.38512


估计的目标函数值 = 7.604

估计的函数计算时间 = 0.057088


mse =

1.3855e+03


r2 =

0.9748


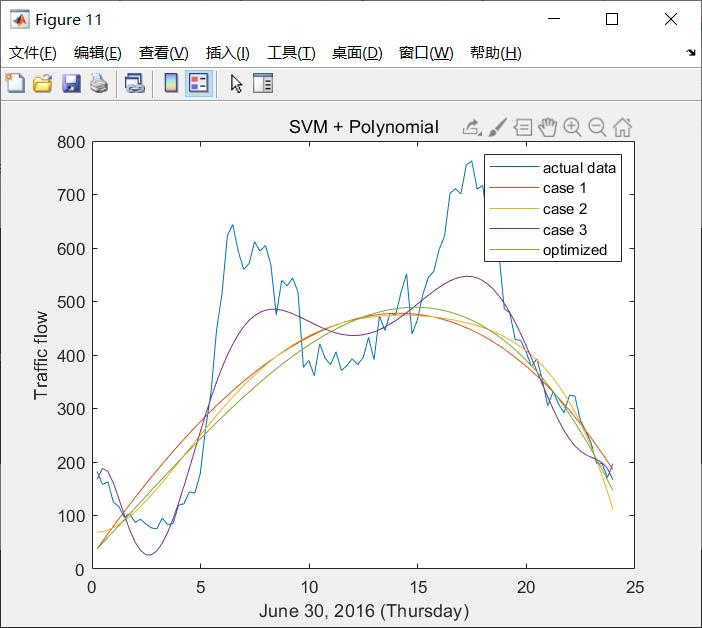
-------Polynomial-------

CASE1 - default:

mse =

1.6898e+04


r2 =

0.6155


CASE2:

mse =

1.5912e+04


r2 =

0.6422


CASE3:

mse =

6.6300e+03


r2 =

0.8565


OPTIMIZED:

|====================================================================================================================|

| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Epsilon |

| | result | log(1+loss) | runtime | (observed) | (estim.) | | | |

|====================================================================================================================|

| 1 | Best | 17.436 | 28.927 | 17.436 | 17.436 | 232.42 | 0.041278 | 0.77342 |

| 2 | Best | 10.42 | 0.071368 | 10.42 | 10.775 | 21.908 | 0.010392 | 12625 |

| 3 | Accept | 10.42 | 0.043085 | 10.42 | 10.42 | 0.0058184 | 18.398 | 3455.5 |

| 4 | Accept | 71.286 | 28.847 | 10.42 | 11.828 | 0.0059341 | 0.0013698 | 2.1953 |

| 5 | Accept | 10.42 | 0.047948 | 10.42 | 10.418 | 24.457 | 0.0030582 | 9739.2 |

| 6 | Accept | 10.42 | 0.037128 | 10.42 | 10.418 | 0.10555 | 1.1212 | 22115 |

| 7 | Accept | 42.845 | 28.004 | 10.42 | 10.415 | 998.17 | 0.0026635 | 83.309 |

| 8 | Accept | 10.42 | 0.038793 | 10.42 | 10.412 | 0.36885 | 0.0012841 | 5198.9 |

| 9 | Accept | 81.729 | 28.321 | 10.42 | 10.418 | 944.81 | 0.0043766 | 0.22306 |

| 10 | Best | 9.571 | 0.40222 | 9.571 | 9.5701 | 172.69 | 0.60399 | 0.77291 |

| 11 | Accept | 9.5906 | 0.17913 | 9.571 | 9.5705 | 0.021205 | 0.14439 | 154.14 |

| 12 | Accept | 10.435 | 0.045818 | 9.571 | 9.5705 | 42.148 | 256.32 | 0.22485 |

| 13 | Accept | 10.42 | 0.036242 | 9.571 | 9.5706 | 65.078 | 995.86 | 9943.1 |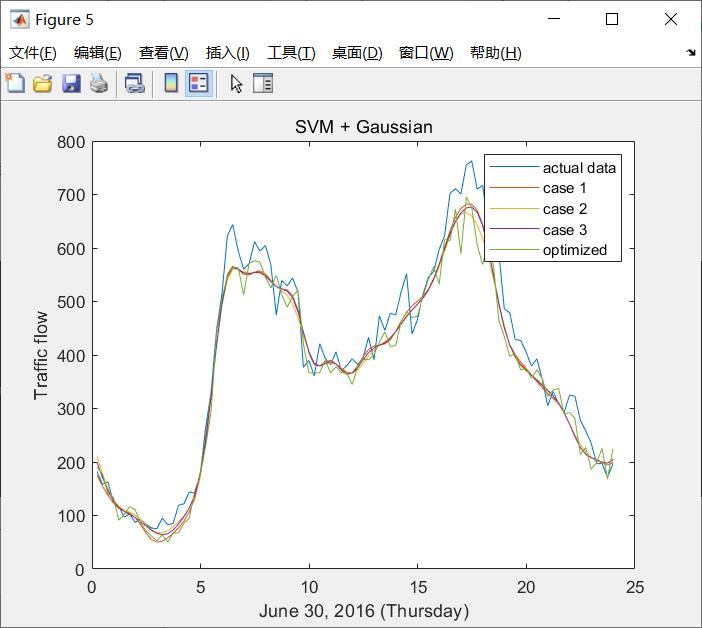

完整代码或仿真咨询QQ1575304183

以上是关于SVM预测基于SVM和LSR交通流预测matlab源码的主要内容，如果未能解决你的问题，请参考以下文章

SVM预测基于蝙蝠算法优化SVM实现预测matlab源码

SVM预测基于麻雀搜索算法优化的SVM数据分类预测matlab源码

SVM时序预测基于matlab鲸鱼算法优化支持向量机SVM时序数据预测含Matlab源码 2250期

SVM预测基于遗传算法优化实现SVM数据分类matlab源码

SVM预测基于粒子群算法优化实现SVM数据分类matlab源码