最优化学习 凸优化问题
Posted Real&Love
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化学习 凸优化问题相关的知识,希望对你有一定的参考价值。
凸优化问题
- 凸优化问题(convex problems)
- 局部最优等同于全局最优(凸优化)
- x ⋆ ∈ S x^{\\star} \\in S x⋆∈S是最优解 ⇔ ∇ f ( x ) T ( x − x ∗ ) ⩾ 0 , ∀ x ∈ S \\Leftrightarrow \\nabla f(x)^{T}\\left(x-x^{*}\\right) \\geqslant 0 ,\\forall x \\in S ⇔∇f(x)T(x−x∗)⩾0,∀x∈S
- 几何解释
- 无约束凸优化问题 m i n f ( x ) minf(x) minf(x)
- 等式约束凸优化 min { f ( x ) ∣ A x = b } \\left.\\min \\{ f(x) \\mid A x=b\\right\\} min{f(x)∣Ax=b}
- 非负约束凸优化 min { f ( x ) ∣ x ⩾ 0 } \\min \\{f(x) \\mid x \\geqslant 0\\} min{f(x)∣x⩾0}
凸优化问题(convex problems)
一般问题描述
min
f
(
x
1
,
…
x
n
)
\\min f\\left(x_{1}, \\ldots x_{n}\\right)
minf(x1,…xn)
s.t.
g
i
(
x
i
,
…
,
x
n
)
⩽
0
,
i
=
1
,
…
,
m
\\text { s.t. } g_{i}\\left(x_{i}, \\ldots, x_{n}\\right) \\leqslant 0, i=1, \\ldots, m
s.t. gi(xi,…,xn)⩽0,i=1,…,m
h
i
(
x
1
,
…
x
n
)
⩽
0
i
=
1
,
…
.
l
.
h_{i}\\left(x_{1}, \\ldots x_{n}\\right) \\leqslant 0 \\quad i=1, \\ldots . l .
hi(x1,…xn)⩽0i=1,….l.

局部最优等同于全局最优(凸优化)
对于凸优化问题,局部最优等同于全局最优
p
r
o
o
f
proof
proof:如下
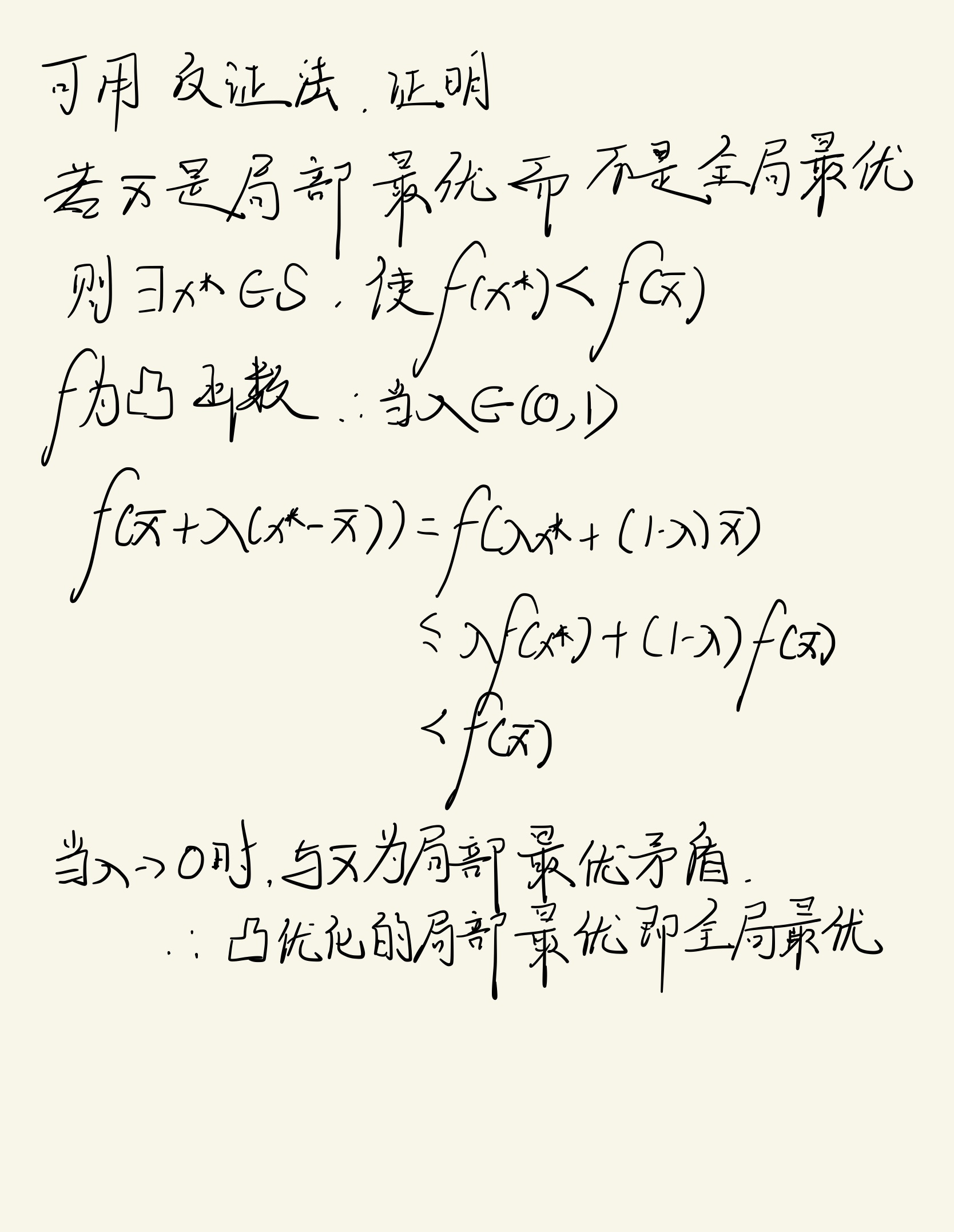
x ⋆ ∈ S x^{\\star} \\in S x⋆∈S是最优解 ⇔ ∇ f ( x ) T ( x − x ∗ ) ⩾ 0 , ∀ x ∈ S \\Leftrightarrow \\nabla f(x)^{T}\\left(x-x^{*}\\right) \\geqslant 0 ,\\forall x \\in S ⇔∇f(x)T(x−x∗)⩾0,∀x∈S
x ⋆ ∈ S x^{\\star} \\in S x⋆∈S是最优解 ⇔ ∇ f ( x ) T ( x − x ∗ ) ⩾ 0 , ∀ x ∈ S \\Leftrightarrow \\nabla f(x)^{T}\\left(x-x^{*}\\right) \\geqslant 0 ,\\forall x \\in S ⇔∇f(x)T(x−x∗)⩾0,∀x∈S
p
r
o
o
f
proof
proof:如下
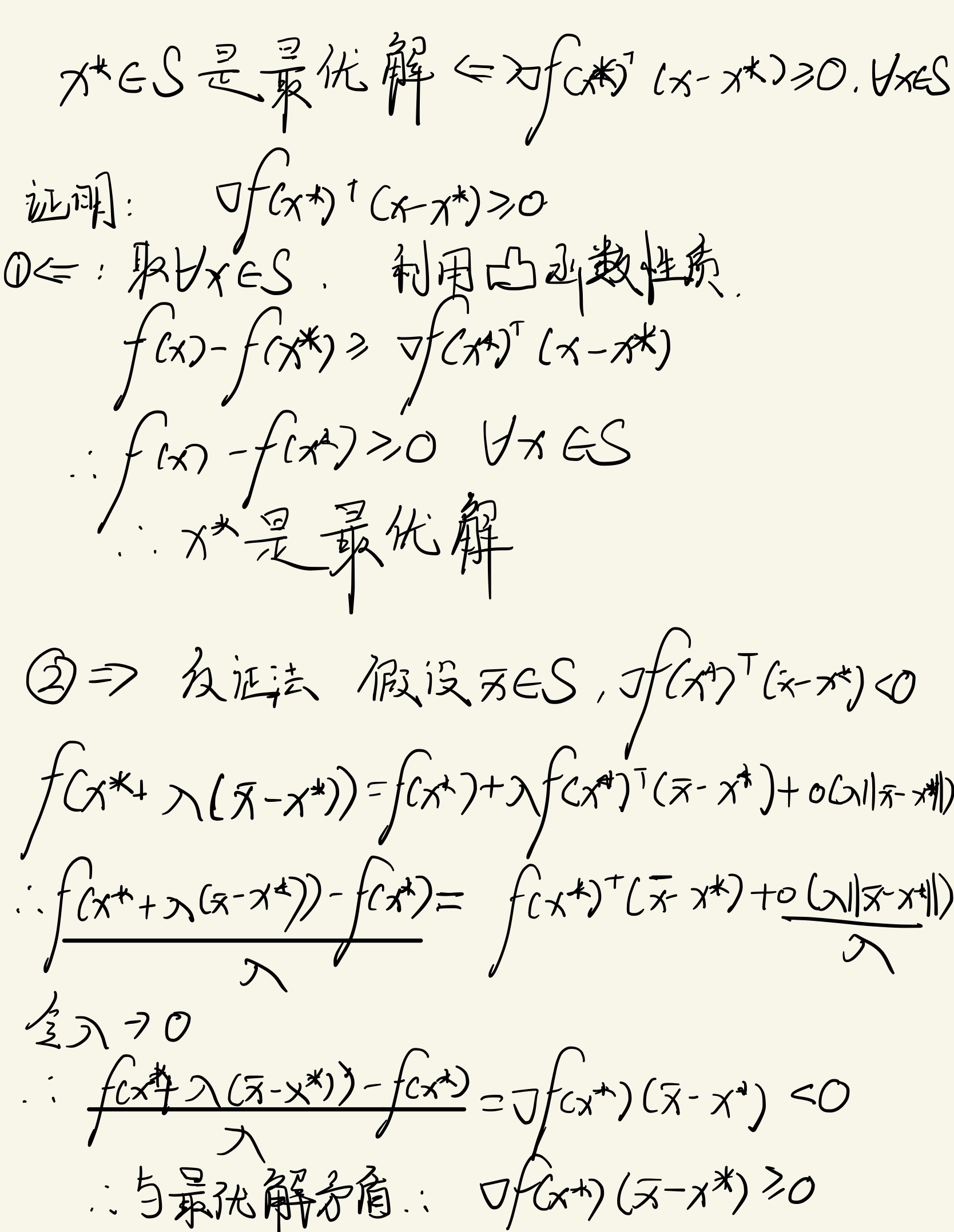
几何解释
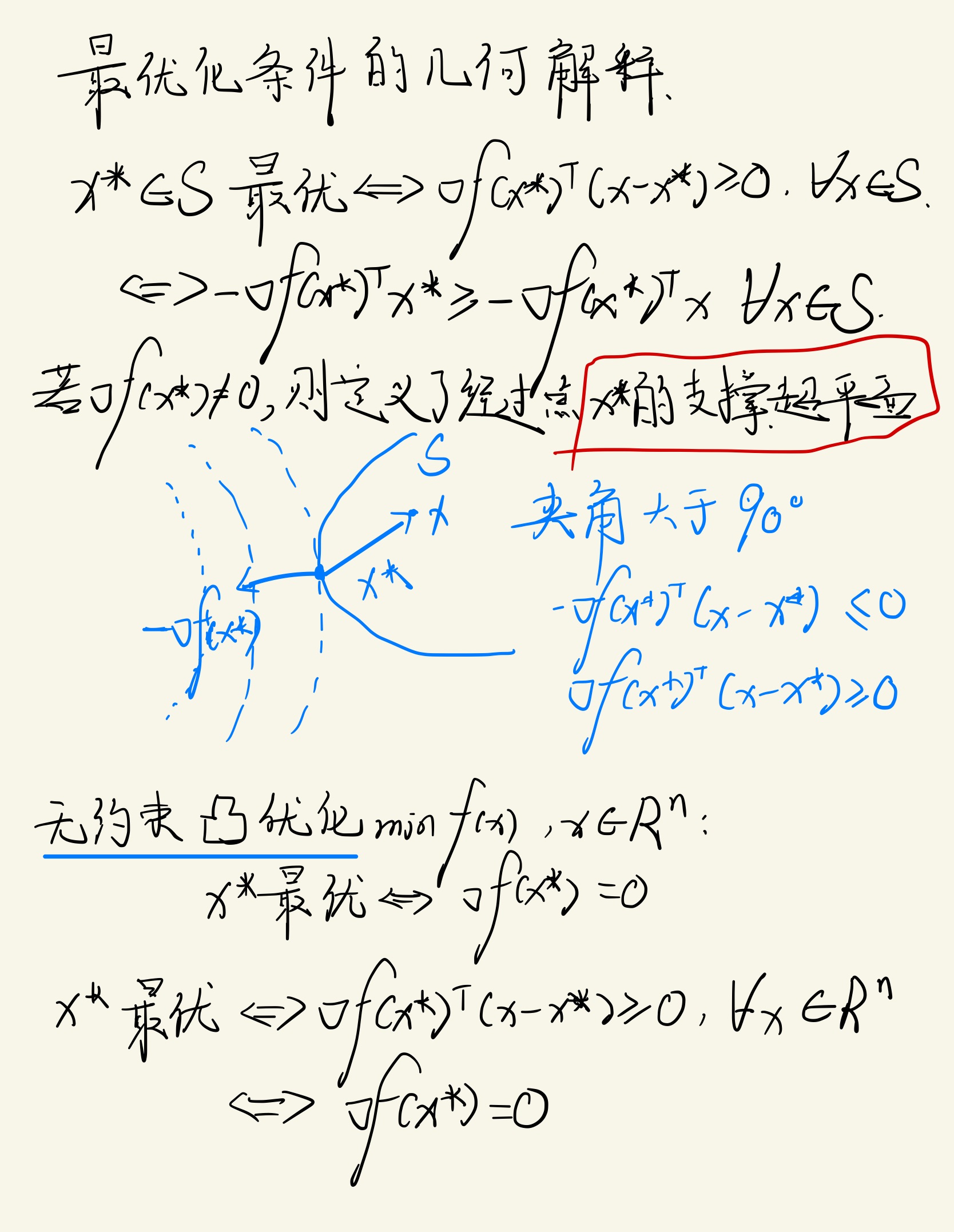
无约束凸优化问题 m i n f ( x ) minf(x) minf(x)
x ∗ 最优 ⇔ ∇ f ( x x ) = 0 x^{*} \\text{最优} \\Leftrightarrow \\nabla f\\left(x^{x}\\right)=0 x∗最优⇔∇f(xx)=0
p
r
o
o
f
proof
proof:如下

等式约束凸优化 min { f ( x ) ∣ A x = b } \\left.\\min \\{ f(x) \\mid A x=b\\right\\} min{f(x)∣Ax=b}
min { f ( x ) ∣ A x = b } \\left.\\min \\{ f(x) \\mid A x=b\\right\\} min{f(x)∣Ax=b}
p
r
o
o
f
proof
proof:如下

非负约束凸优化 min { f ( x ) ∣ x ⩾ 0 } \\min \\{f(x) \\mid x \\geqslant 0\\} min{f(x)∣x⩾0}
p
r
o
o
f
proof
proof:如下

以上是关于最优化学习 凸优化问题的主要内容,如果未能解决你的问题,请参考以下文章