最优化学习 算法收敛性
Posted Real&Love
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化学习 算法收敛性相关的知识,希望对你有一定的参考价值。
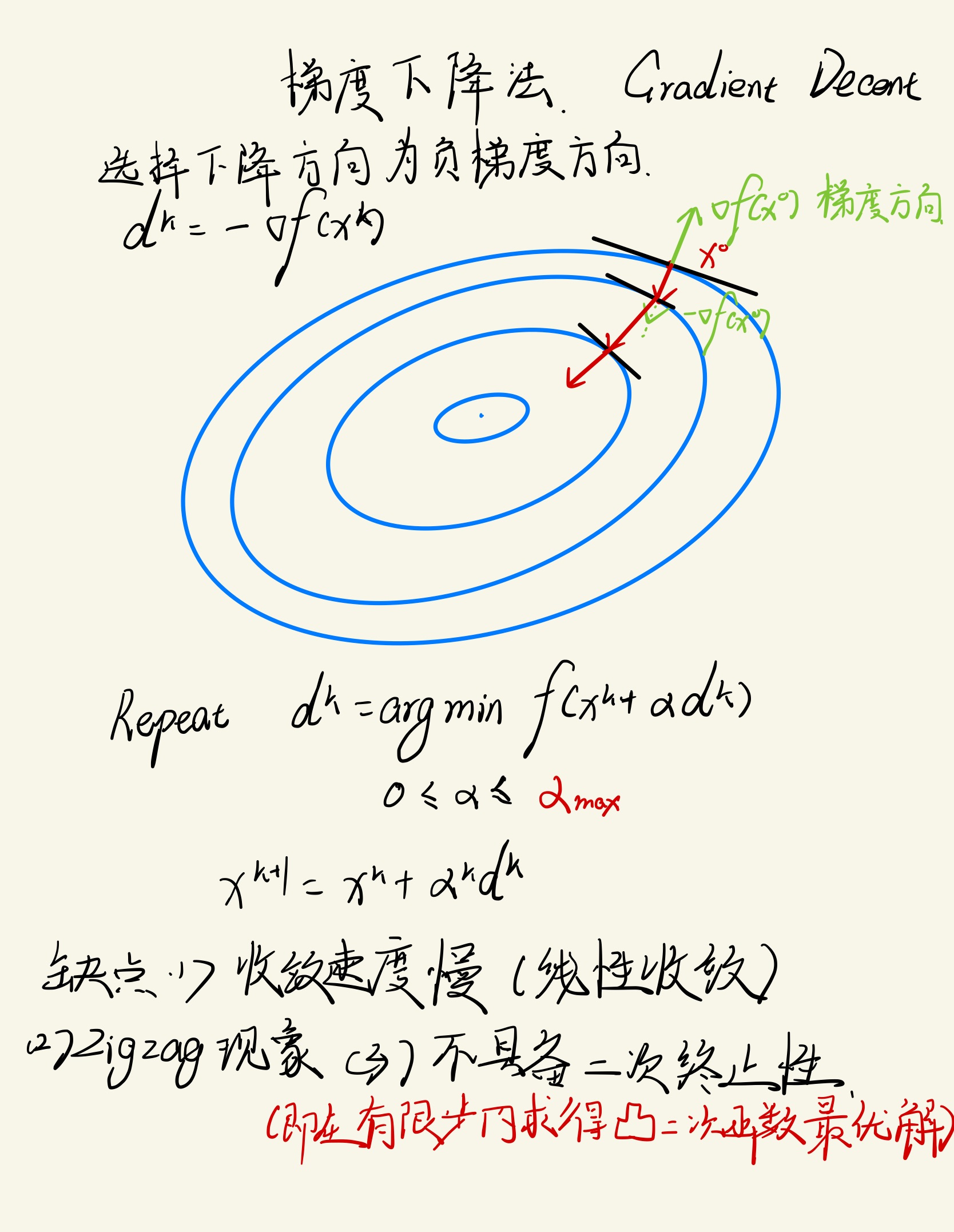
梯度下降法
d k + 1 = − ∇ f ( x k ) d^{k+1}=-\\nabla f\\left(x^{k}\\right) dk+1=−∇f(xk) f ( x k + 1 ) − P ∗ f ( x k ) − P ∗ ≤ 1 − m M \\frac{f\\left(x^{k+1}\\right)-P^{*}}{f\\left(x^{k}\\right)-P^{*}} \\leq 1-\\frac{m}{M} f(xk)−P∗f(xk+1)−P∗≤1−Mm ≤ 1 − min { 2 m γ α max , 2 m γ β M } \\leq 1-\\min \\left\\{2 m \\gamma \\alpha_{\\max }, \\frac{2 m \\gamma \\beta}{M}\\right\\} ≤1−min{2mγαmax,M2mγβ} K ∼ log ( f ( x k ) − P ∗ ) 线 性 收 敛 K \\sim \\log \\left(f\\left(x^{k}\\right)-P^{*}\\right) \\quad线性收敛 K∼log(f(xk)−P∗)线性收敛
分析算法收敛性 - 精确线搜索exact line search
∀
x
∈
d
o
m
f
,
M
I
⪰
∇
2
f
(
x
)
⪰
m
I
\\forall x \\in d o m f, M I \\succeq \\nabla^{2} f(x) \\succeq m I
∀x∈domf,MI⪰∇2f(x)⪰mI
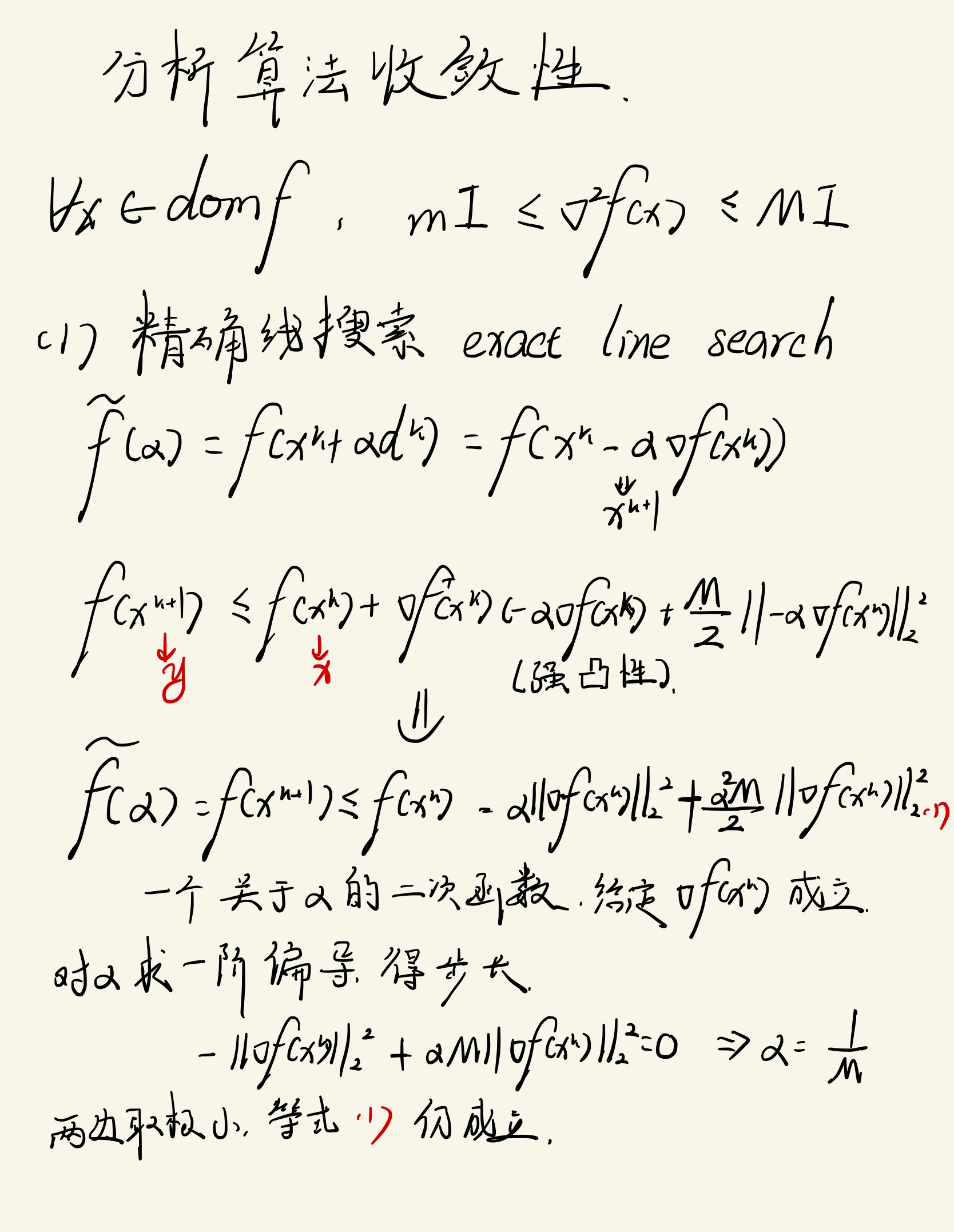

分析算法收敛性 - 非精确线搜索Inexact line search(Amijo Rule)


以上是关于最优化学习 算法收敛性的主要内容,如果未能解决你的问题,请参考以下文章