数据结构与算法概念与理解（更新中）

Posted 2021-06-10 dxj1016

1、数据结构与算法

编程语言、数据结构与算法的关系

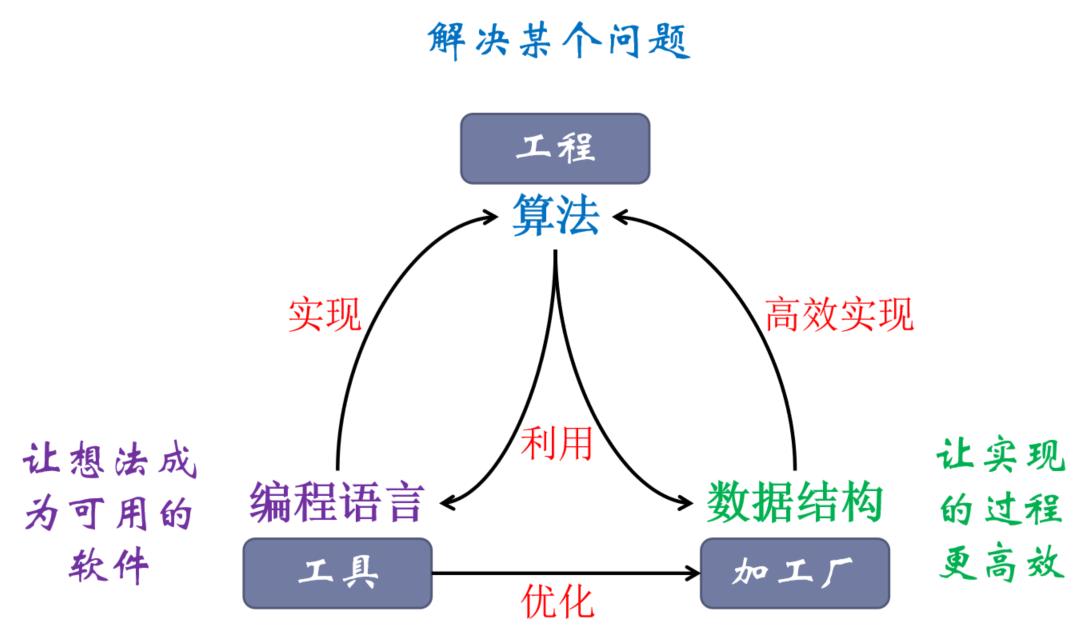
两个层次的掌握：

• 知其然：掌握算法分析方法（第2章）和八大算法（蛮力法、分治法、减治法、动态规划法、贪心法、回溯法、分支限界法和概率法）的设计思路和经典例子
• 知其所以然：熟知和理解各种算法的设计思路，应用于解决实际问题

程序=算法+数据
算法：程序的灵魂，解决一个问题采用的方法和步骤

1.1、算法特性

一个好的算法通常具有以下特性：

• 正确性：得到正确或者近似的结果
• 健壮性：抵抗尽可能多的错误或不合法输入的影响
• 可理解性：一看就懂，一懂就能实现
• 抽象分级：简练，数据合理分类
• 高效性：时间复杂度（快），空间复杂度（省）

1.2、算法的描述方法

• 自然语言：文字描述
• 流程图：用框图和流程线描述
• 结构化流程图：改进的流程图
• N-S图：简洁的流程图
• 伪代码：擅于设计算法时对算法的描述
• 计算机语言：用语言实现算法（c语言或java语言）

1.3、查找问题的经典算法

• 二分查找
• 顺序查找
• 串匹配问题
• 折半查找
• 二叉查找树

1.4、排序问题的经典算法

• 选择排序
• 起泡排序
• 归并排序
• 快速排序（重要）
• 插入排序
• 堆排序

1.5、图问题

• 哈密顿回路
• TSP问题（特殊的哈密顿回路：路径最短）
• 最短路径问题（单源点最短路径问题、多段图最短路径问题、多源点最短路径问题）
• 图着色问题
• 最小生成树问题

1.6、组合问题

• 0/1背包问题
• 最大子段和问题
• 八皇后问题

1.7、集合问题

• 最近对问题
• 凸包问题

2、时间复杂度

2.1、概念

• 执行算法的快慢与什么有关：硬件因素、软件因素

• 排除软硬因素，算法的执行速度随执行语句数量增加而就增加。

• 基本语句：最重要的语句，主要来源于循环结构（循环体内若有条件结构，则条件部分为基本语句，条件部分若包含循环结构，要具体分析访问循环结构的次数。）
  
  

• 输入规模：影响基本语句的执行次数的变量，通常来说，输入规模越大，算法的计算复杂度越长
  

• 时间复杂度函数T（n）：算法基本语句的执行次数，变量n为输入规模
• 时间复杂度O(n)
• 非递归算法的时间复杂度分析
  
  

2.2、非递归算法的时间复杂度

2.3、递归算法的时间复杂度

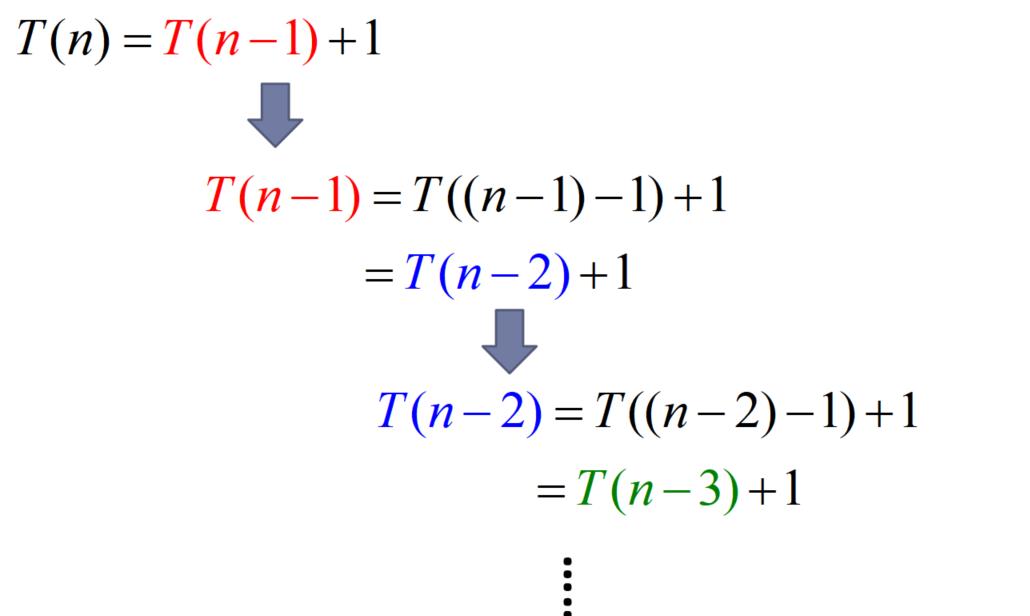
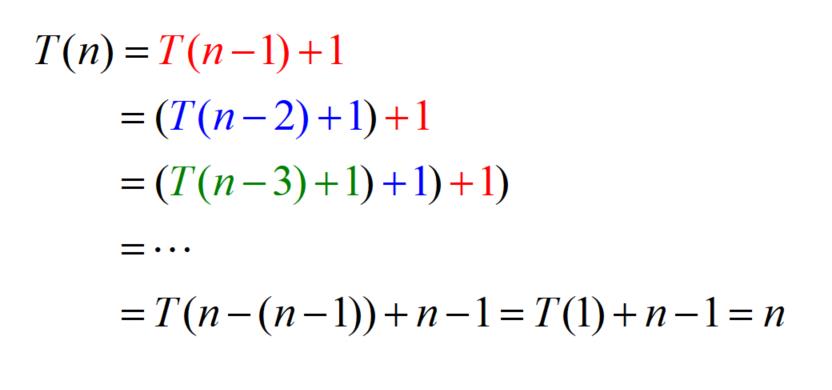
2.4、算法的空间复杂性分析

3、蛮力法

3.1、设计思路

• 基本思想：遍历所有取值，选出符合任务要去的解。
• 最简单，最容易想到的方法，几乎能解决所有的问题。
• 时间复杂度往往最高
• 蛮力法是最笨的方法。

3.2、步骤

3.3、应用

3.4、查找问题

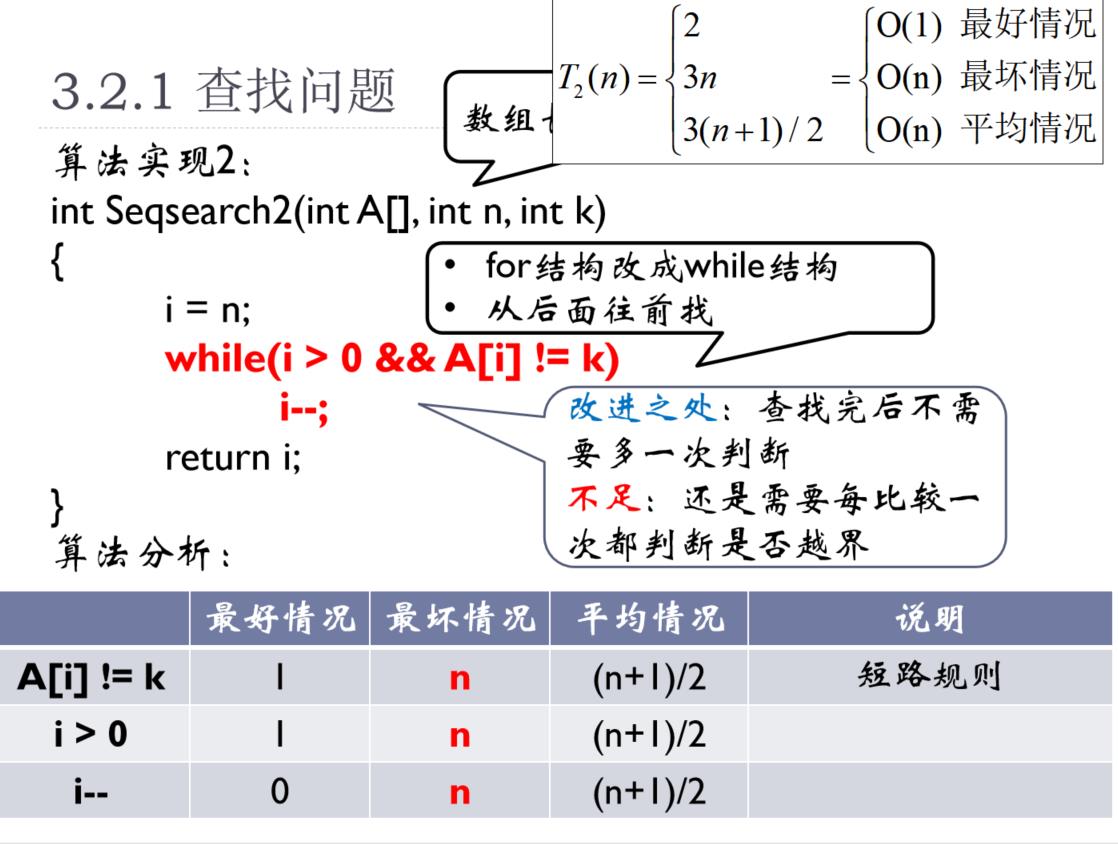
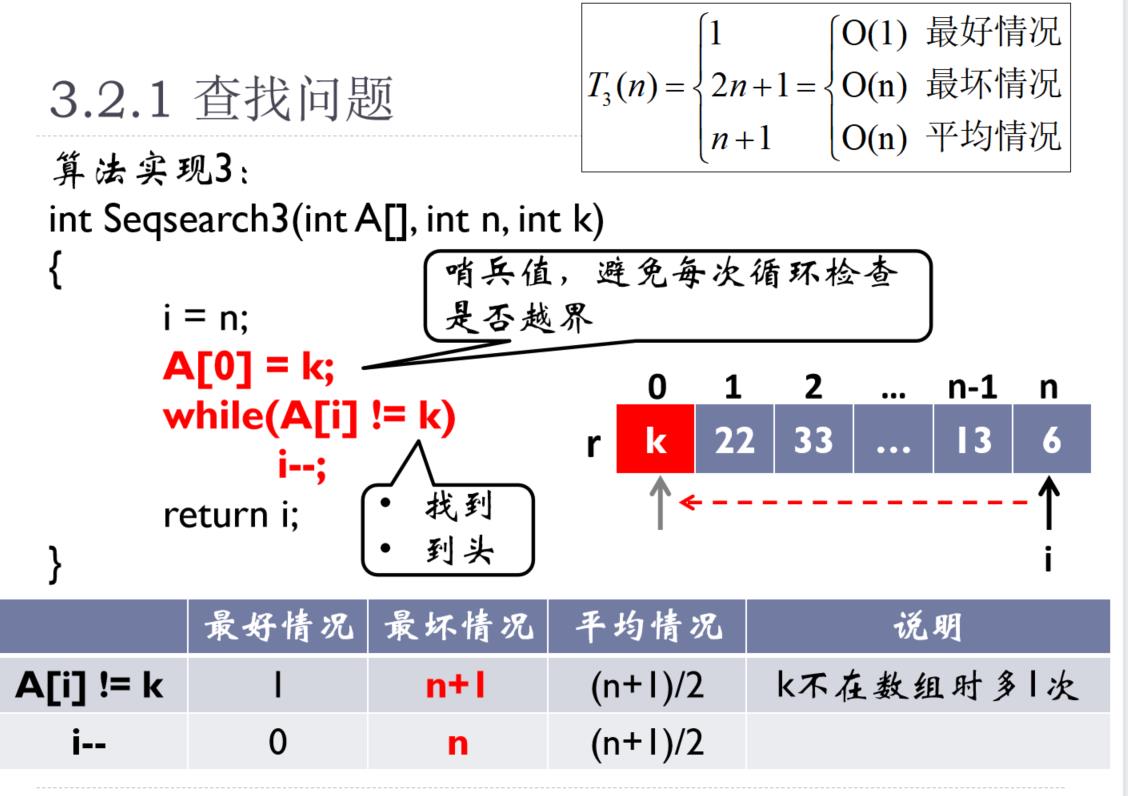
3.4.1、顺序查找

顺序查找

• 可从头向尾查找，也可从尾向头查找
• 若从尾向头查找，可通过设置哨兵值减少越界的判定
• 最好：O(1)；最坏：O(n)；平均：O(n)
  
  
  
  

3.4.2、串匹配问题

• BF算法
  （1）每次匹配失败，模式串往后移一位，从头开始进行下一次匹配
  （2）时间复杂度为O(mn)，与主串和模式串长度有关
• KMP算法
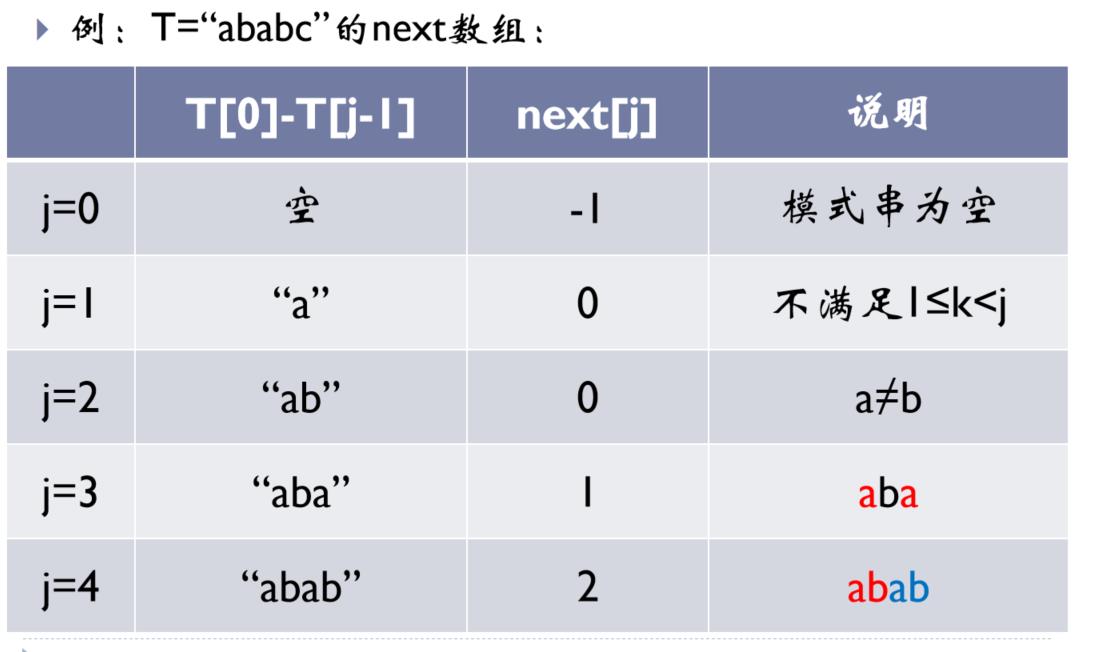
  （1）利用模式串本身的相似性，去除多余的匹配
  （2）next数组的创建
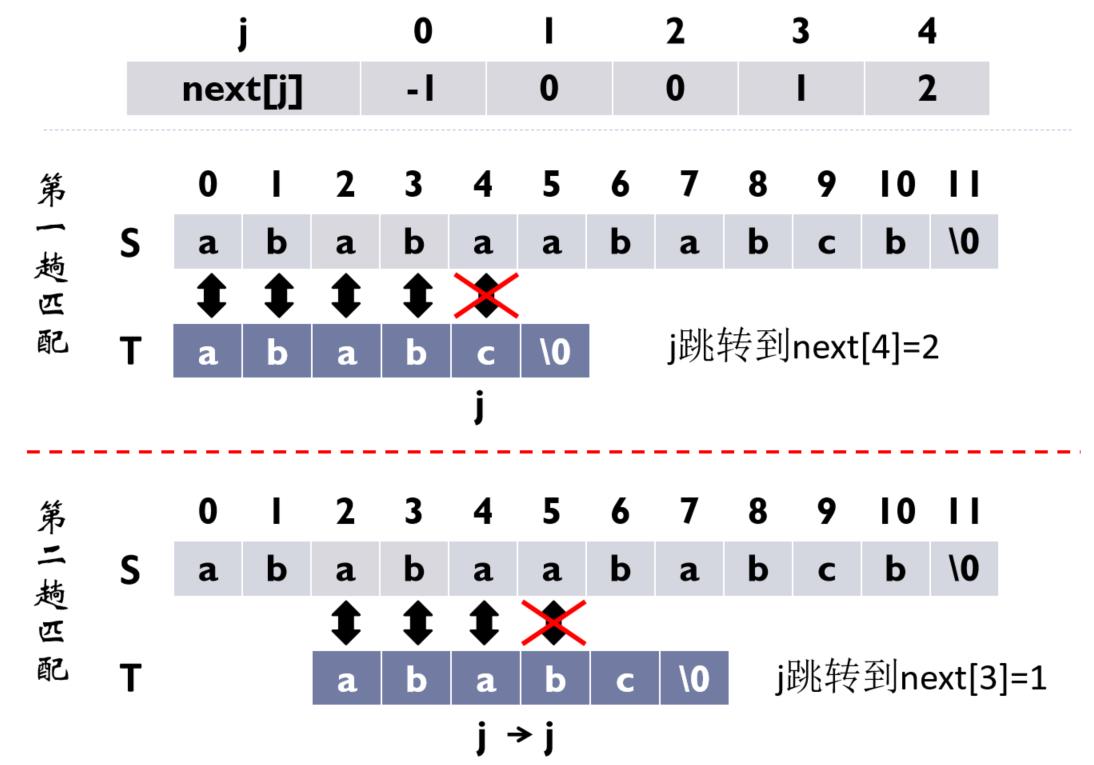
  （3）匹配算法
  当匹配不成功时，主串不回溯，模式串回溯到next[j]，其中j是指不匹配的字符在模式串中的位置
  若next[j]=-1，主串下标往向移一位，模式串从头开始匹配
  （4）时间复杂度：O(m+n)，生成next的函数采用《阅读材料》的方法

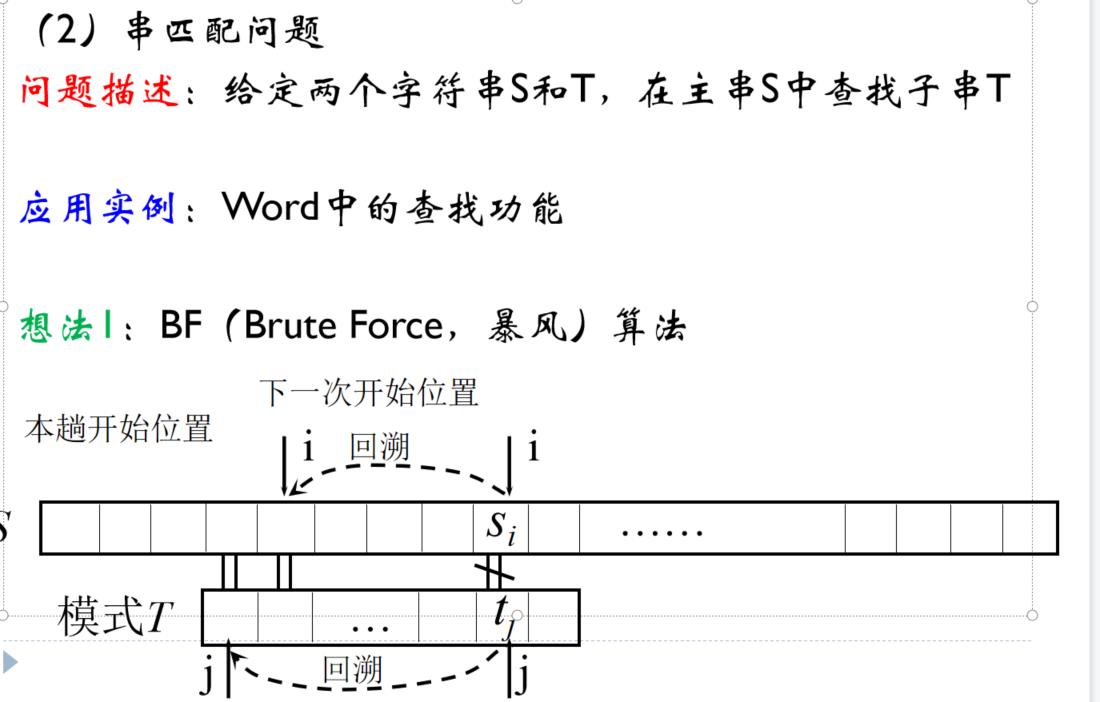
暴风BF算法过程：使用子串T去匹配原串S中的元素，T从头开始，S也从头开始，T匹配的元素跟S元素不匹配时，T从头开始，S从上次开始的下个元素开始，基础使用T所有元素去匹配S。直到找到子串T为止。

KMP算法过程：

• 求next数组：下标为0的元素值为-1，下标为1的元素值为0，下标为2的元素的值为取子串中的前两个元素看可不可弄出对称元素，对称元素个数为下标为2的元素值，例如aa，则值为1，aba值1，aaaa值为2；后面的计算跟下标为2一样。
• 匹配过程：子串和文本都从头开始，计算到不匹配的元素的时候，看子串那个不匹配的元素的下标为多少，取子串下标元素的next值，比如在子串的第四个元素也是下标为3的元素不匹配，则next[3]=1；得出的next数组的值作为子串T从文本S的哪个位置开始，比如next[3]=1;则从文本S的第二个元素开始匹配T。
  
  

3.5、排序问题

3.5.1、选择排序

基本思想：

• 将序列划分成有序区（左边）和无序区（右边）
• 初始时，有序区为空，无序区为序列全部
• 每一次选择出无序区中最小元素，与无序区中第1个元素交换，成为有序区的最后一个元素

真题：对数据48,70,8,30,23,11,15进行选择排序，写出每趟的结果
解：每次都从无序区中选择最小元素与无序区第一个元素交换成为有序区末尾
初始： （）48,70,8,30,23,11,15
第1趟：（8）70,48,30,23,11,15
第2趟：（8,11）48,30,23, 70,15
第3趟：（8,11,15）30,23, 70,48
第4趟：（8,11,15,23）30, 70,48
第5趟：（8,11,15,23,30）70,48
第6趟：（8,11,15,23,30,48）70

3.5.2、起泡排序

基本思想：

• 将序列划分成有序区（右边）和无序区（左边）
• 初始时，有序区为空，无序区为序列全部
• 每一次“起泡”相邻元素依次两两比较，将较大/小者交换到后面，成为有序区的第一个元素

例：采用起泡排序法对数据48,70,8,30,23,11,15进行升序排序，写出每趟的结果
解：
初始： 48,70,8,30,23,11,15（）
第1趟起泡：
48,70,8,30,23,11,15
48,8,70,30,23,11,15
48,8,30,70,23,11,15
48,8,30,23,70,11,15
48,8,30,23,11,70,15
48,8,30,23,11,15,（70）
第2趟起泡：
8,48,30,23,11,15,（70）
8,30,48,23,11,15,（70）
8,30,23,48,11,15,（70）
8,30,23,11,48,15,（70）
8,30,23,11,15,（48, 70）
第3趟起泡：
8,30,23,11,15,（48, 70）
8,23,30,11,15,（48, 70）
8,23,11,30,15,（48, 70）
8,23,11,15,（30,48, 70）
第4趟起泡：
8,23,11,15,（30,48, 70）
8,11,23,15,（30,48, 70）
8,11,15,（23,30,48, 70）
第5趟起泡：
8,11,15,（23,30,48, 70）
8,11,（15,23,30,48, 70）
第6趟起泡：
8,（11,15,23,30,48, 70）

3.6、组合问题

3.6.1、0/1背包问题

问题描述：给定n个不同重量不同价值的物品和一个容量一定的背包，设计方案使得在不超出背包容量的前提下，装进背包的物品总价值最高。

• 如果用0表示物品不装进去，1表示物品装进去，则问题变成对每个物品指定0或者1的过程，所以称为0/1背包问题
• 背包问题是0/1背包问题的一般化，即物品可以部分装到包里

蛮力法求解基本思想：穷举所有装包的方案，选择价值最高的一个

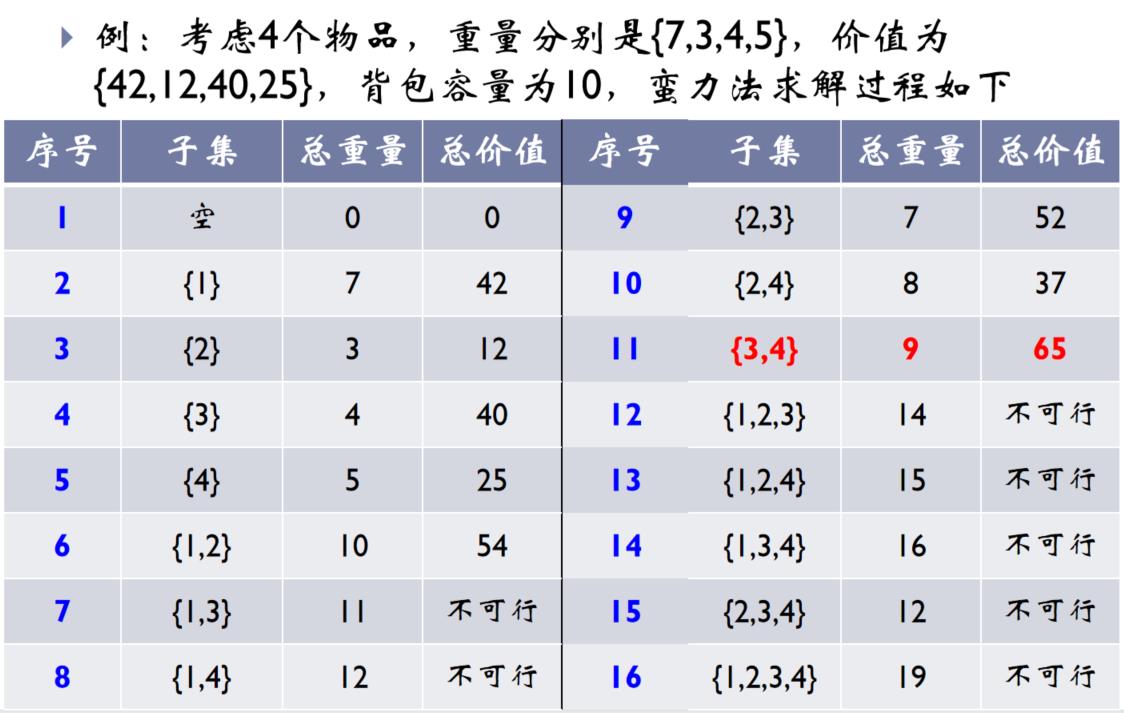
3.6.2、任务分配问题

问题描述：假设有n个任务分给n个人执行，每个人只能执行一个任务且执行不同任务的成本不同，求一个分配方法，使得总成本最小

想法：列出所有可能的分配方案，逐个去检验其成本，选择成本最小的一个方案

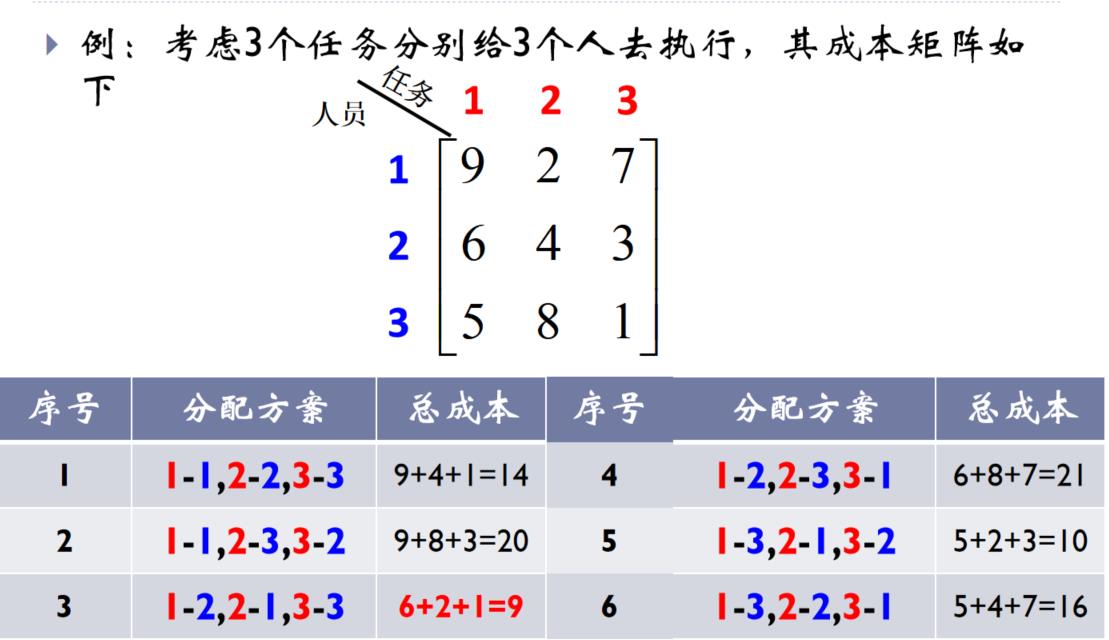
3.7、图问题

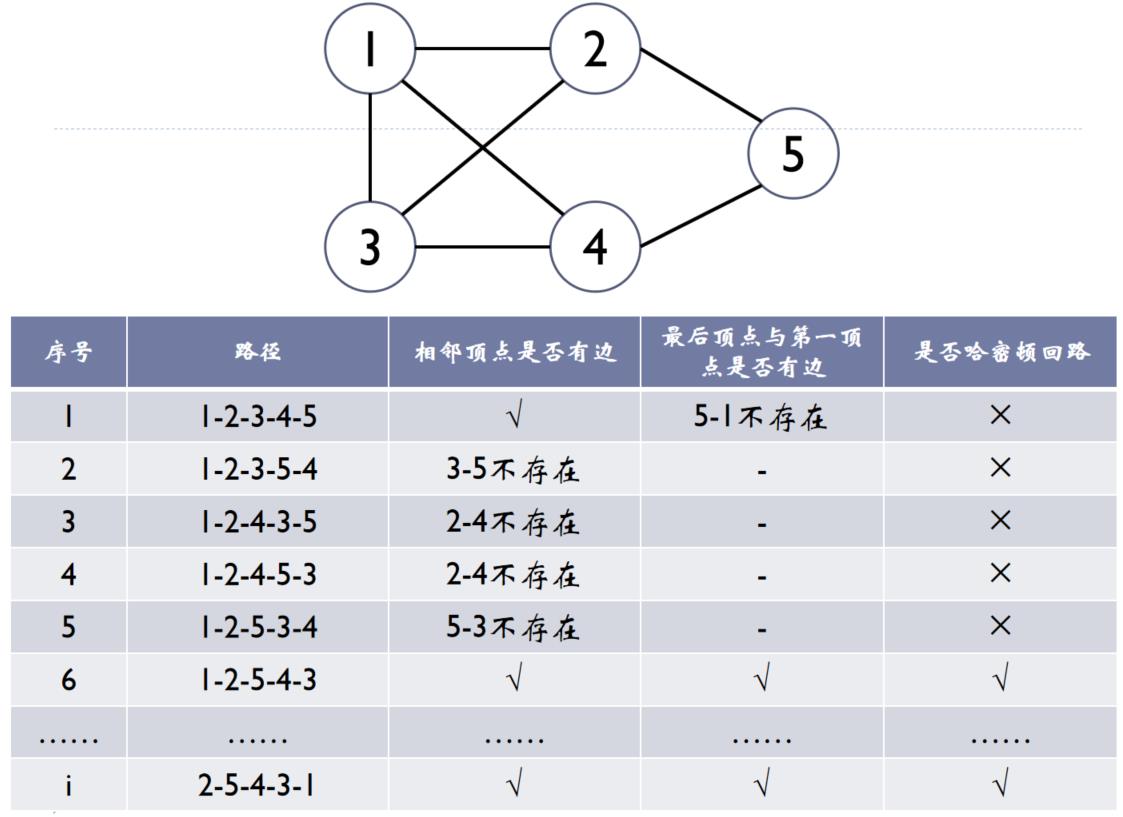
3.7.1、哈密顿回路问题（周游世界问题）

问题描述：在给定的N个城市以及城市间的通路，要求找出一条线路，使得从一个城市出发，经过每个城市恰好一次，然后回到出发城市。


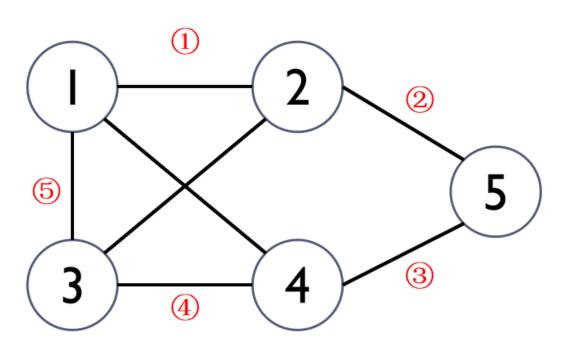
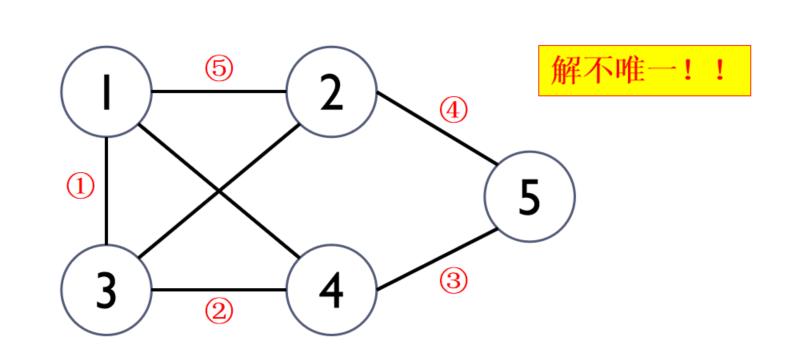
想法：

• 不考虑结点与结点之间是否连通，n个结点遍历一遍再回到原点的可能性共有n!个；例：3个城市，可能的哈密顿回路有以下3!=6条，分别是：
  1→2→3→1
  1→3→2→1
  2→1→3→2
  2→3→1→2
  3→1→2→3
  3→2→1→3
• 依次检验各种方案是否符合哈密顿回路的条件：
  （1）相邻顶点之间存在边
  （2）最后一个顶点与第一个点之间存在边

3.7.2、TSP问题

问题描述： TSP(Travelling Salesman Problem)，遍历n个城市，且要求所走路程最短，是一个特殊的哈密顿回路问题

TSP问题 VS 哈密顿问题

• 相同点：都要求从一个城市出发，遍历所有城市一次，再回到第一个城市
• 不同点：哈密顿问题在无向图中进行；TSP问题在带权无向图中进行（因为要算最短路程）

想法：与哈密顿回路想法相近
（1）穷举所有遍历各城市的方案
（2）分别检查当前方案是否构成哈密顿回路，如果是，则计算当前方案的路程，并检查是否路程最短

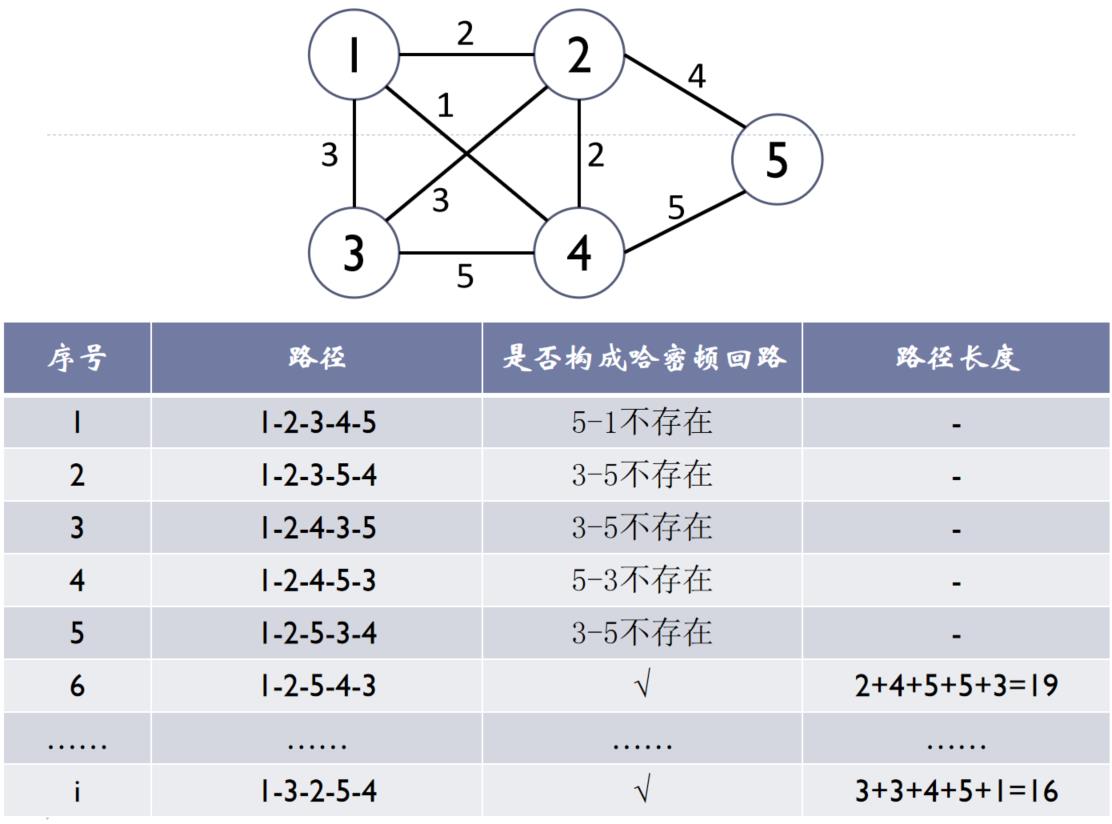
算法分析
（1）对指定出发城市的TSP问题，总共的方案数为：(n-1)!个
（2）每个方案需要检查是否为哈密顿回路，需要循环最多n条路径
（3）总计算量T(n)=n*(n-1)!=n!=O(n!)

注意： 在各方案中，有一半路径相同，只是方向相反，比如：1-3-2-5-4-1和1-4-5-2-3-1，因此可以只算一半的路径，但时间复杂度仍为O(n!)

3.8、几何问题

3.8.1、最近对问题

问题描述：在一堆散点集中，找出距离最短的一对点

想法： 对所有点两两计算其欧几里德距离，取其中最短的一对点作为输出
两个点(xA,yA)和(xB,yB)的欧几里德距离d(A,B)为：

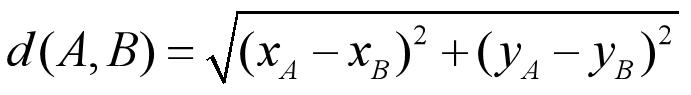
3.8.2、凸包问题

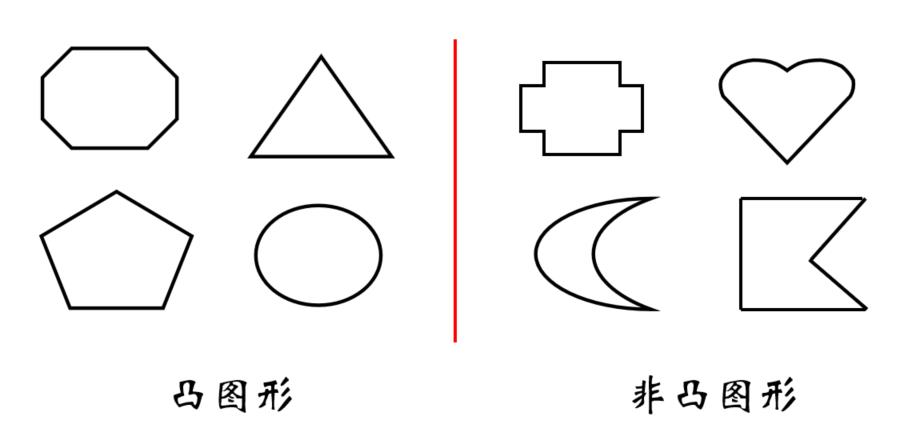
Before 凸包，什么是凸？

定义： 一个图形是凸图形，当且仅当图形内任意两点的连线，都包含在该图形内


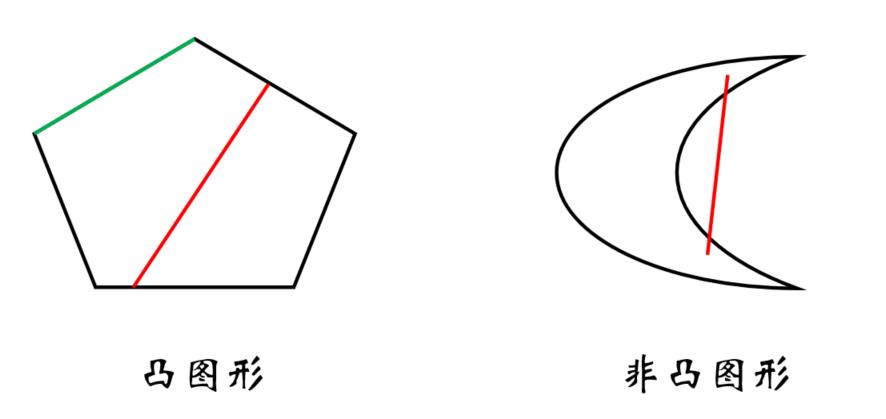
凸包问题：点集的最小凸多边形构造问题

• 在点集中找出一个子集，使得这些子集中各点相连构成一个凸图形（凸多边形），刚好把所有点集包含
• 下图p1-p8构成了点集的一个凸包，称为极点
  
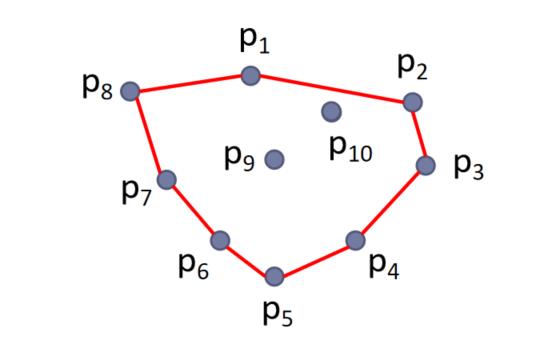
  想法：
• 考虑构成凸包的边的特点：所有点集都位于该边划分出来的一边
• 设p1和p2的坐标分别是(x1,y1)和(x2,y2)，则该两点确定的直线方程为：
  
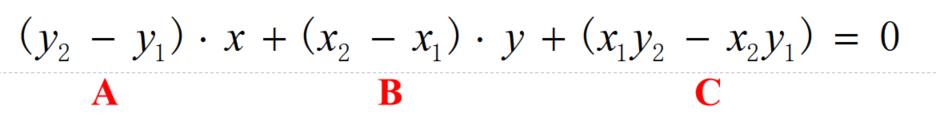
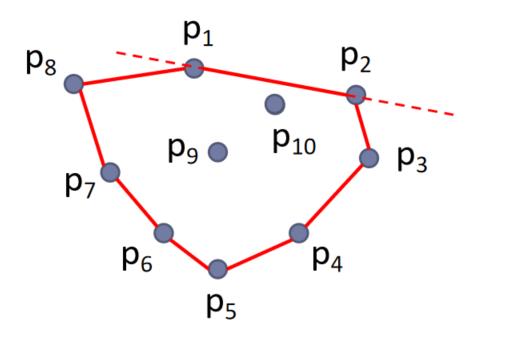
• 设点集中的两个点，其确定的直线方程为Ax+By+C=0。若所有点集都在该直线的一边，即Ax+By+C≥0或Ax+By+C≤0，则该两点为凸包上的两个极点
  

3.9、总结

（1）蛮力法的基本思想：
遍历所有自变量的取值，搜索满足任务要求的解

（2）蛮力法的设计思路：
确定自变量及其变化范围
根据任务已知条件去除冗余的穷举量

（3）蛮力法的特点：简单、慢、万能

4、分治法

4.1、分治法的基本思想

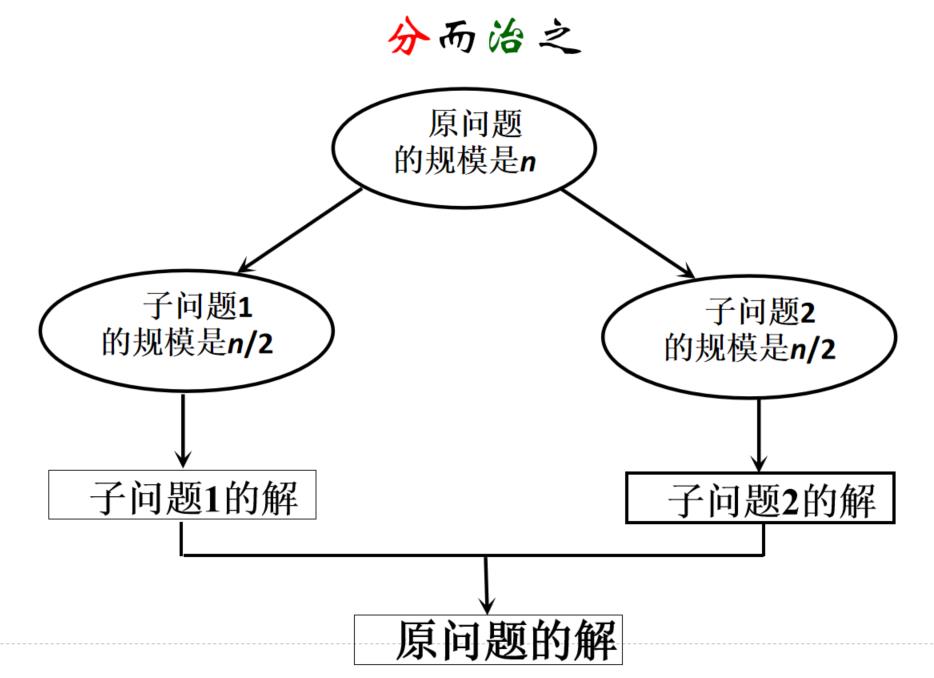
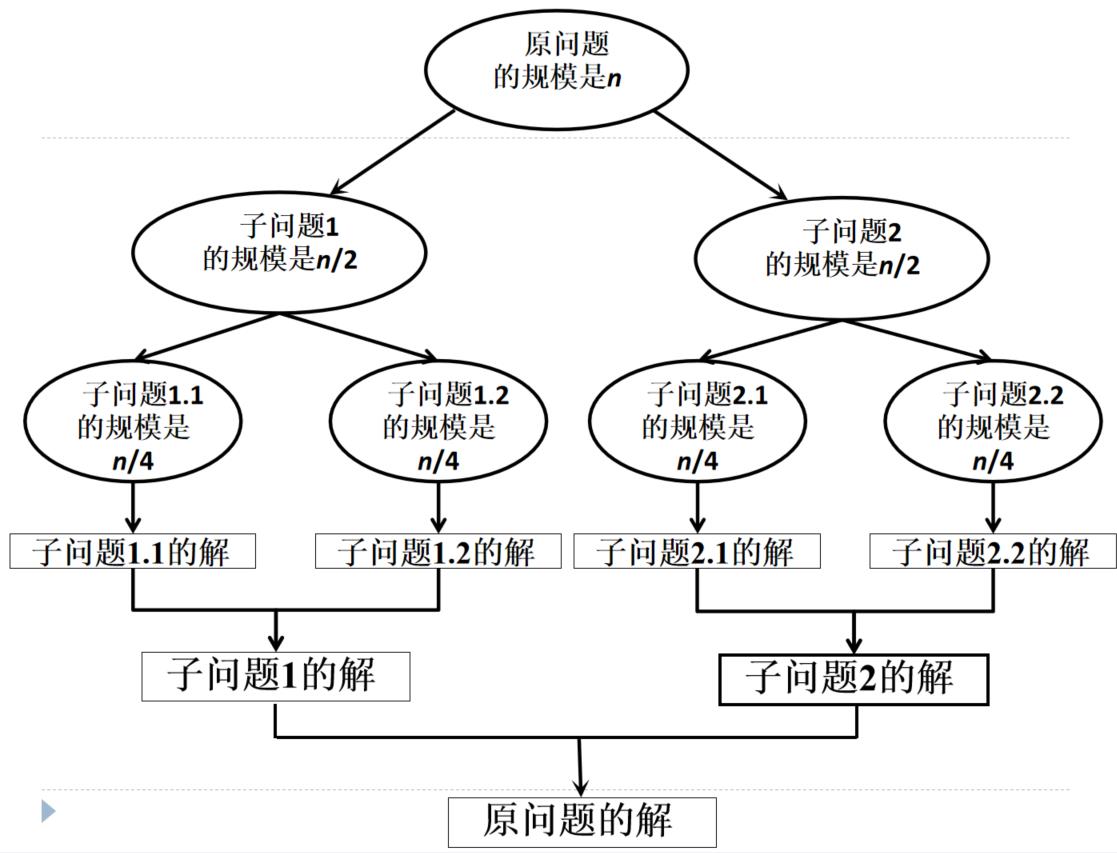
分治法求解问题的主要步骤：划分，求解，合并
（1）问题划分。将规模为n的问题划分成k个子问题
细节：

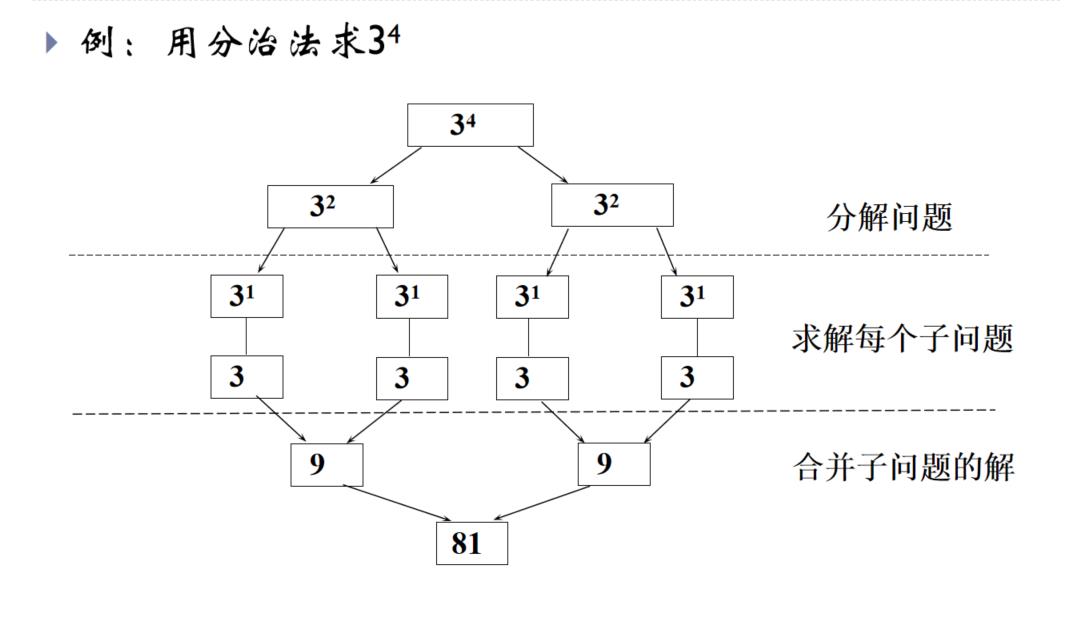
• 如果子问题规模仍然很大，可以再继续划分3^2可继续划分成2个 3的1次方相乘
• 每个子问题的规模尽可能相等（平衡子问题），便于用相同的方法去求解子问题3的4次方划分成3的2次方，再划分成3的1次方，都在算3的幂次方
• 每个子问题间尽可能独立（独立子问题），若不独立，需要另外处于公共子问题（最大子段和）

（2）求解子问题。各子问题的求解方法相同，通常采用递归方法实现。f(n)→f(n/2)→f(n/4)……
（3）合并子问题的解。将各子问题的解逐层合并，得到问题的最终解

4.2、排序问题

4.2.1、归并排序

基本思想：
将序列划分成两个长度相等的子序列，分别进行排序，最后将两个有序序列合并

步骤：

• 将序列分成两段相等长度的子序列
• 从两段序列的第一个元素开始比较两段序列的元素，取当前较小的值为新序列的元素
• 将采纳的子序列下标向后移动，采纳的元素添加到新的队列中。
• 当其中一个序列全部移动到新序列后，剩余序列直接拷贝
  
  真题：对数据48,70,8,30,23,11,15,28进行归并排序，写出每趟的结果
  ① 划分：
  48,70,8,30 23,11,15,28
  48,70 8,30 23,11 15,28
  48 70 8 30 23 11 15 28

② 求解子问题，并合并子问题：
第一趟： 48 70 8 30 23 11 15 28
第二趟： 48,70 8,30 11,23 15,28
第三趟： 8,30,48,70 11,15,23,28
第四趟： 8,11,15,23,28,30,48,70

4.2.2、快速排序

基本思想：
（1）划分：选定一个数做为轴值，把序列分成比轴值小（左边）和比轴值大（右边）两个子序列

• 选定第一个元素作为轴值，下标用i标记，后面的元素用j标记；从后面和前面比较，后面的值比轴值大就后面的下标向前移动一位，如果后面的比前面的小，那么两个元素交换位置，前面的下标向后移动一位；交换后之前是轴值有j标记，所以下次比较如果后面的大于前面的就是i向后移动不是j向前移动。
• 当i和j重合时结束
  
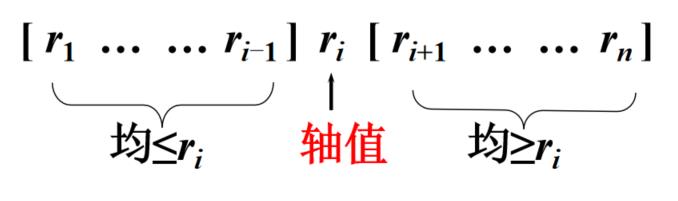
  （2）求解子问题：分别对两个子序列进行轴值划分
  （3）合并：不需要合并！！

关于快速排序的你可能不知道的事
（1）快速排序的适用场合
根据时间复杂度分析，快速排序对已有序（不管是正序还是逆序）的序列，效率最差。

（2）快速排序属于“有序度增长法”，虽然每次划分得到的序列并非有序，但每次划分实质上是找出轴值在排序后的位置，即每次划分是对轴值进行排序

（3）假如某次划分后，轴值所在位置为i，实质上表明该轴值在序列中是第i小的值（注意，这里说的序列是参与划分的序列），因此可借助快速排序的划分操作实现“求序列第i小数”

例：采用排序方法对以下序列进行排序，写出每一趟的排序结果：
48,70,8,30,23,11,15,28
解：
初始： 48,70,8,30,23,11,15,28
第一趟： [28,15,8,30,23,11],(48),[70]
第二趟： [11,15,8,23],(28),[30],(48),[70]
第三趟： [8],(11),[15,23],(28),[30],(48),[70]
第四趟： (8,11),[15,23],(28),[30],(48),[70]
第五趟： (8,11,15),[23],(28),[30],(48),[70]
第六趟： (8,11,15,23,28),[30],(48),[70]
第七趟： (8,11,15,23,28,30,48),[70]
第八趟： 8,11,15,23,28,30,48,70

加粗 表示轴值；
圆括号表示已经排好的数
中括号表示待排序的区

4.3、组合问题

4.3.1、最大子段和问题

问题：
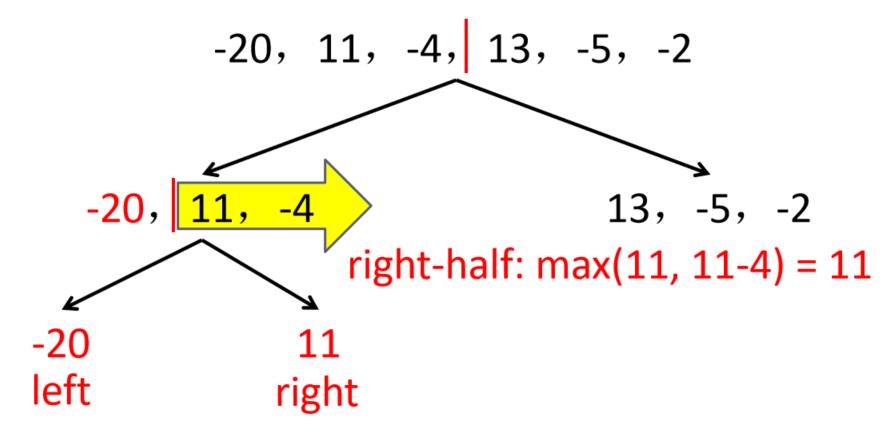
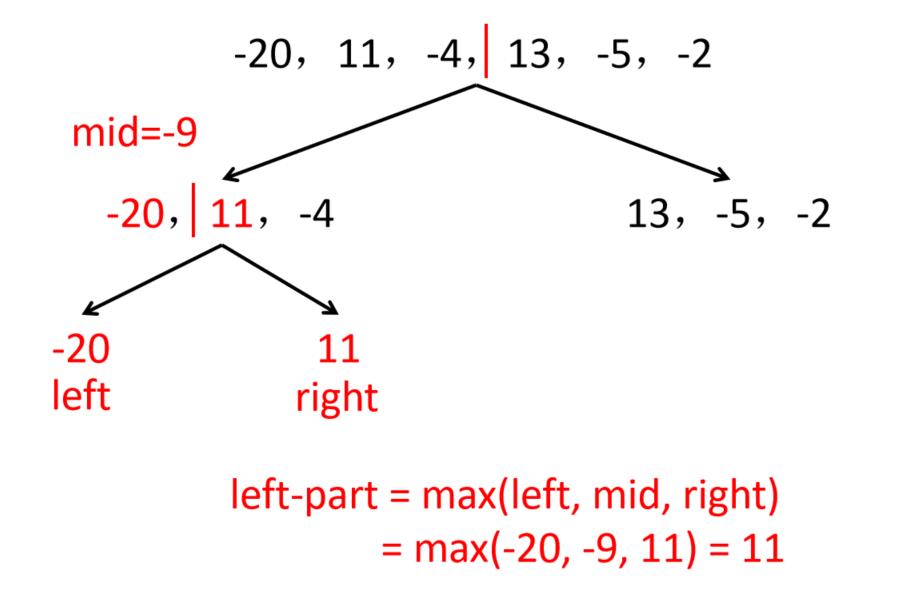
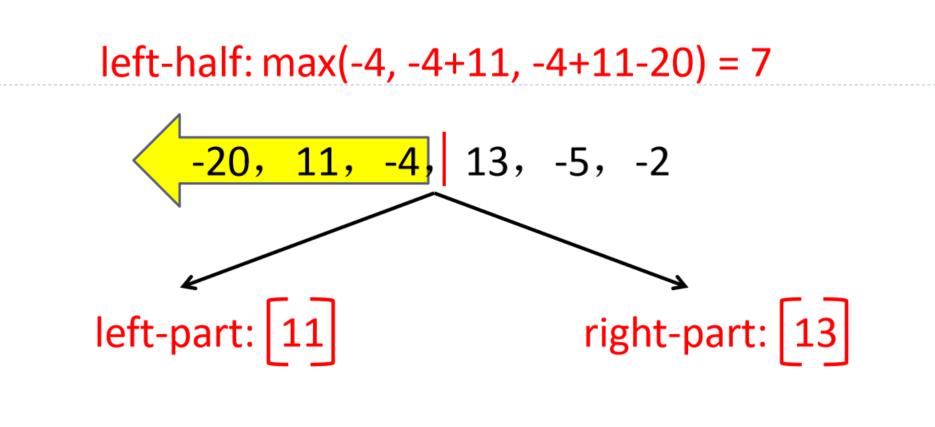
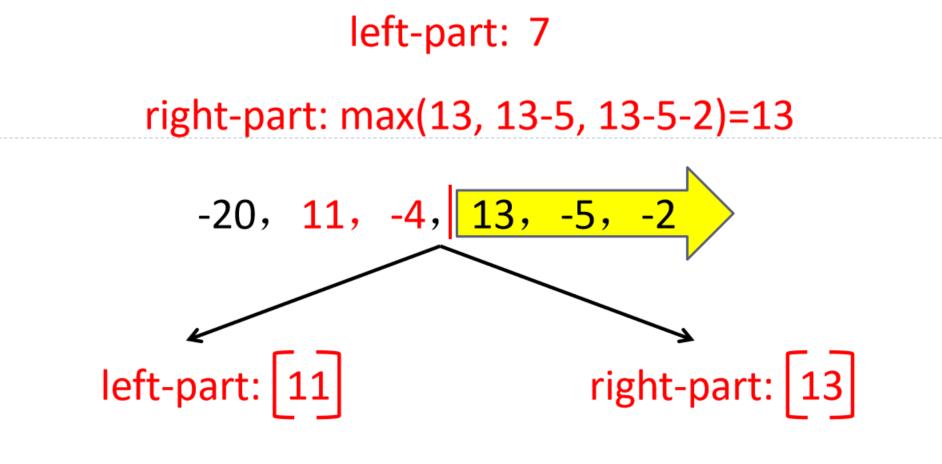
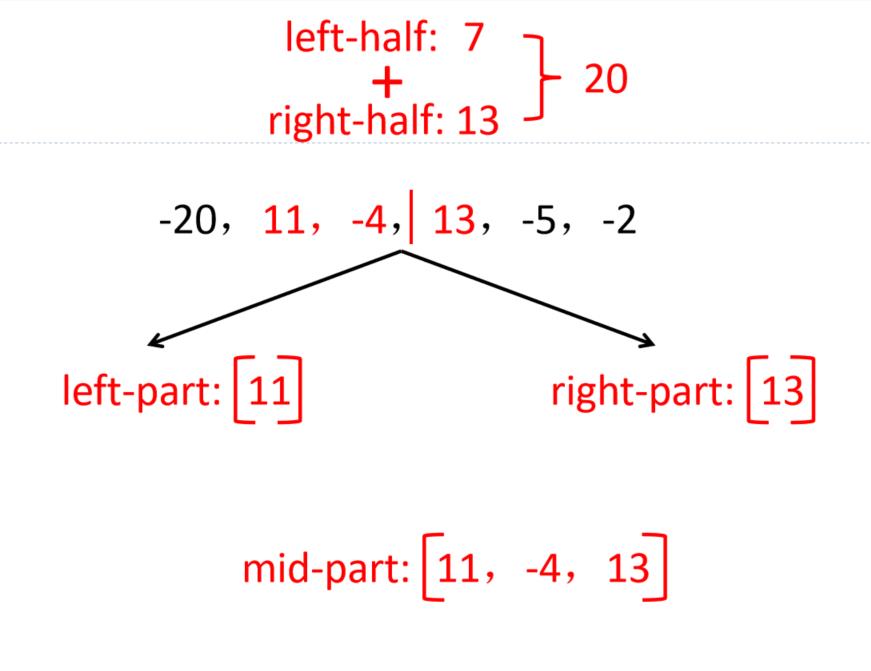
给定由n个整数（可能有负整数）组成的序列，的到其中一个连续的子序列（子段），使得该子段的和是所有连续子段中最大，如-20，11，-4，13，-5，-2

采用分治法求解最大子段和问题步骤：
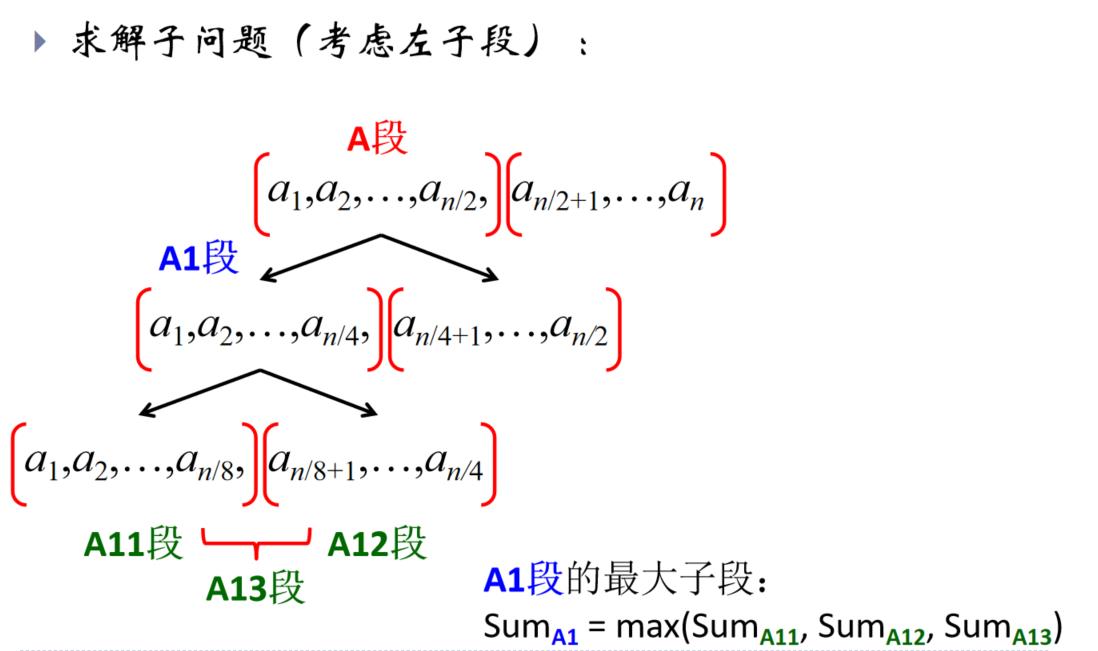
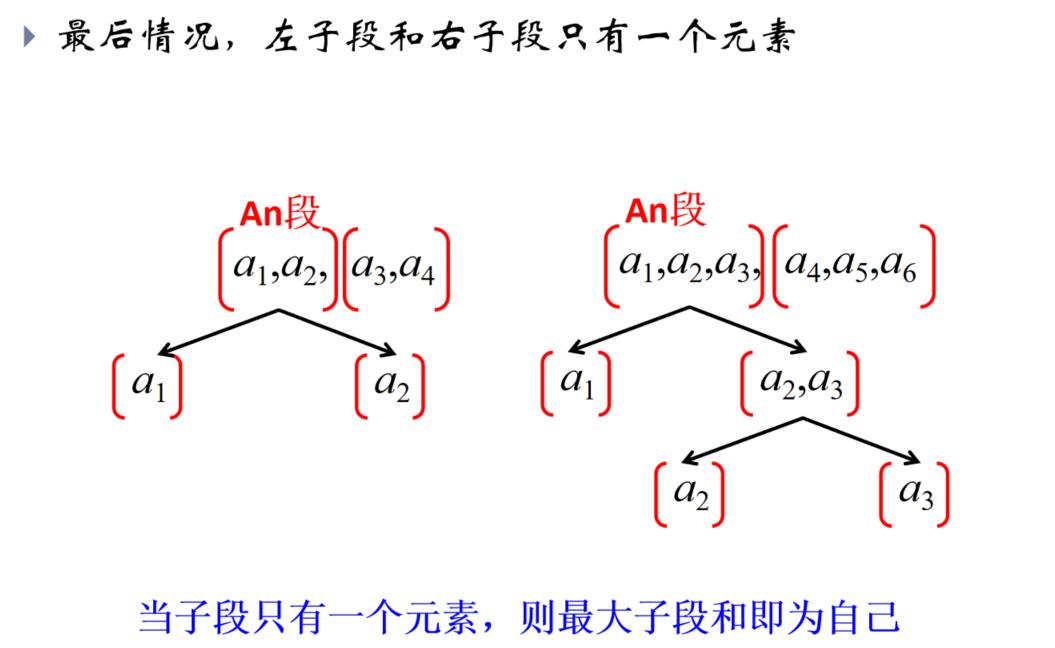
（1）划分：将序列划在长度相等的两段

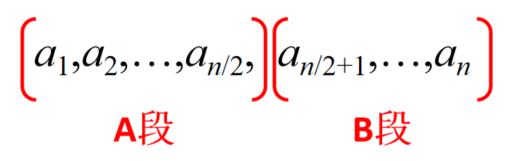
3种情况：
① 最大子段和出现在A段；
② 最大子段和出现在B段；
③ 最大子段和一部分在A段，另一部分在B段。

想法：

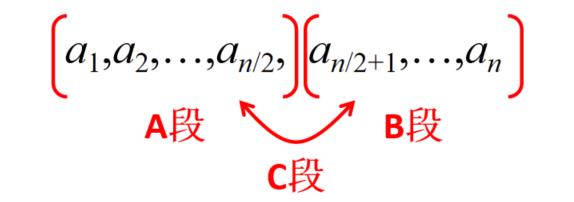
（1）分别找出上述3种情况的最大子段和：设A段的最大子段和为SumA，B段的为SumB，跨越AB段的最大子段和为SumC
（2）整段序列的最大子段和必为上面3个子段和的最大值，即MaxSum = max(SumA, SumB, SumC)



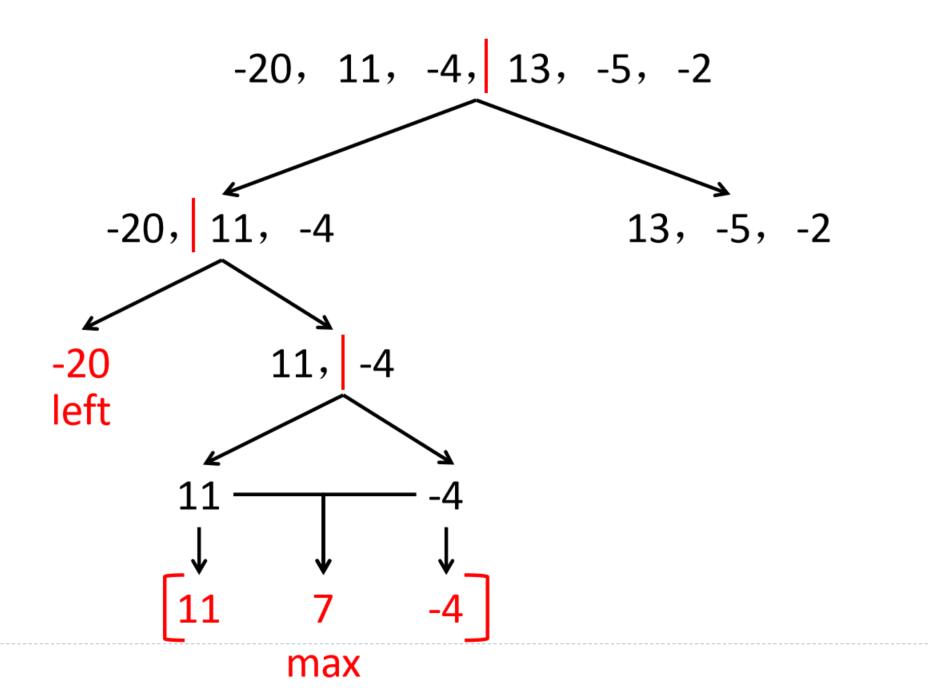
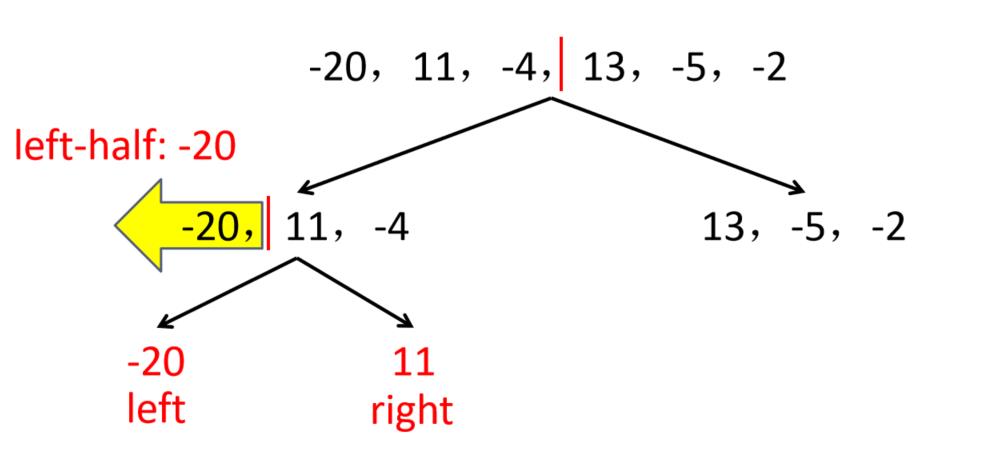
例：求以下序列的最大子段和
-20，11，-4，13，-5，-2
解：先求左子段，再求右子段，最后求跨子段

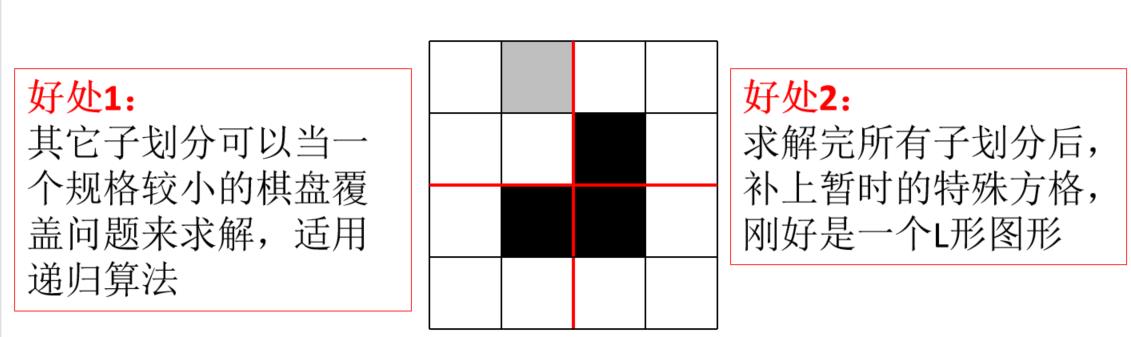
4.3.2、棋盘覆盖问题

问题描述：
在一个2k*2k个方格组成的棋盘中，恰有一个方格与其它方格不同，要求用不同角度的L形图形填充剩下的方格


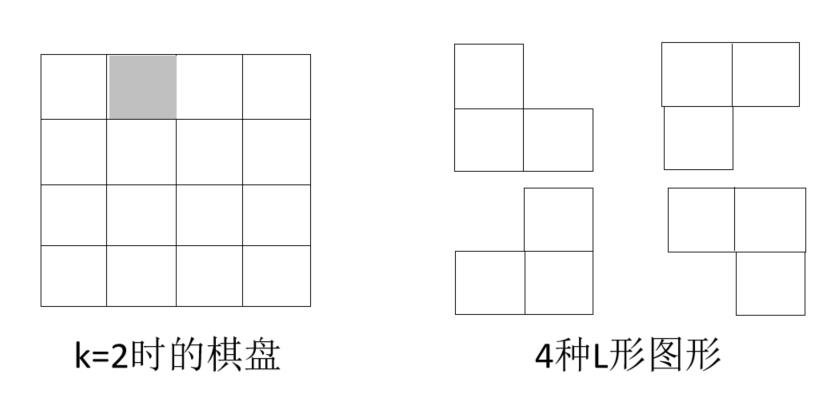
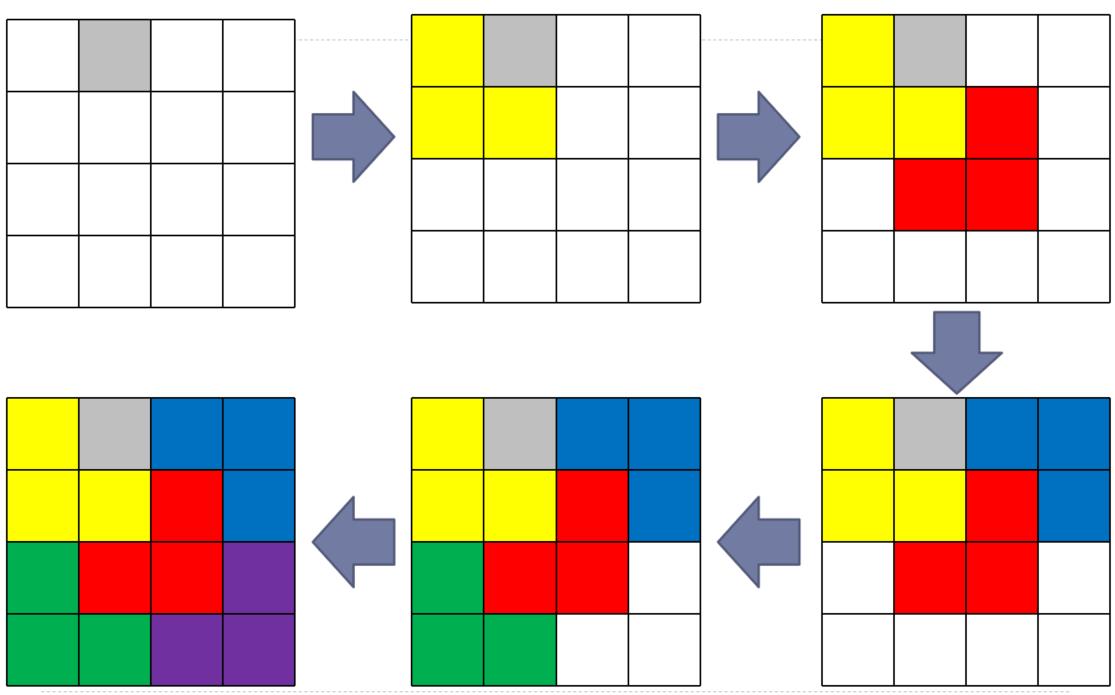
想法：
（1）划分：将棋盘划分成相等的四份，特殊的方格只会落在其中一份中
（2）将有特殊方格的一份继续平分为四份。经过多次划分后，肯定会出现一个L形图形和一个特殊方格的情况

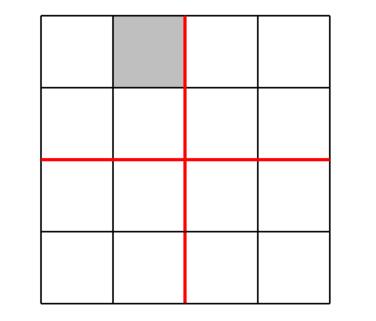
（3）为了让上述划分同样适用于其它方格，在每次划分后，对没有特殊方格的子划分接合处的方格暂时设为特殊方格

4.4、几何问题

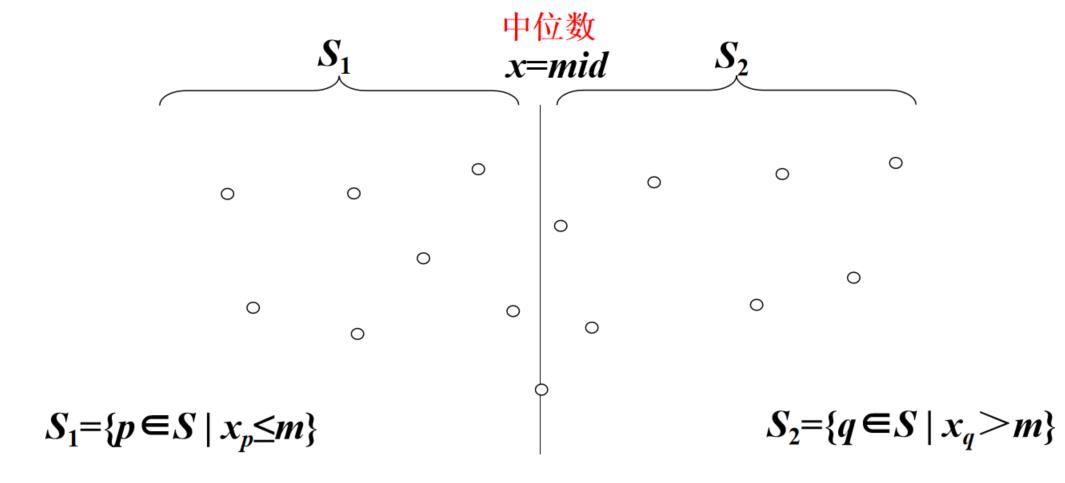
4.4.1、最近对问题

（1）划分：将点集划分成基本相等的两个子集

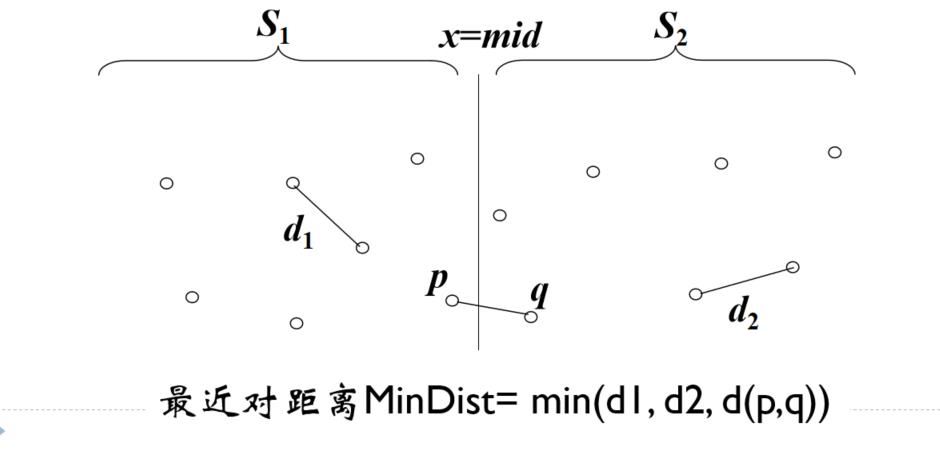
（2）子问题求解：
① 最近对在S1中，最小距离为d1
② 最近对在S2中，最小距离为d2
③ 最近对的两个点分别在S1和S2中，最小距离为d(p,q)

子问题①和②采用递归方法求解：
double closest(point s[], int low, int high){
if 子集中只剩两个点P1(x1, y1)，P2(x2,y2)
计算并返回两点的距离(即最小距离)，算法结束；

if 子集中有三个点P1(x1,y1)，P2(x2,y2)，P3(x3,y3)
{ 分别计算三个点相互的距离d(P1,P2), d(P1,P3)和d(P2,P3)
返回三个距离中的最小值，算法结束；
}
注意：要特别处理三个点的情况，是因为三个点继续划分，会出现孤立点，不能形成距离

4.4.2、凸包问题

4.5、总结

分治法的基本思想：将原问题划分成若干个规模较小的子问题，通过求解各子问题来得到原问题的解

分治法的基本步骤：
（1）划分：
（1.1）平衡子问题：子问题规模尽量相同
（1.2）独立子问题：子问题尽量相互独立
（2）求解子问题：采用递归方法
（3）合并子问题的解

5、减治法

基本思想
用减治法求两个有序序列的中位数（中间大的数）
比如：S1={11,13,15,17,19}， S2={2,4,6,8,20}
则S1和S2的中位数为两个数列合并后的中位数，即：S1∪S2={2,4,6,8,11,13,15,17,19,20}
中位数为11

想法：
（1）分别求出两个序列的中位数，记为a和b。
（2）两个序列的中位数可能出现在三种位置：
① 若a=b，则a或b即为两个序列的中位数；
比如：S1={11,13,15,17,19}，其中位数为a=15；
S2={2,4,15,18,20}，其中 位数为b=15。
S1∪S2={2,4,11,13,15, 15,17,18,19,20}
两个序列的中位数为a或b=15
② 若a<b，则中位数出现在[a, b]之间：
比如：S1={11,13,15,17,19}，其中位数为a=15；
S2={16,18,20,28,40}，其中 位数为b=20。
S1∪S2={11,13,15, 16,17,18,19,20,28,40}
两个序列的中位数在[15,20]范围内
注意：只需要考虑S1序列中位数(15)以后的数，及S2序列中位数(20)以前的数
③ 若a>b，则中位出现在[b, a]之间：
比如：S1={16,18,20,28,40}，其中位数为a=20；
S2={11,13,15,17,19}，其中 位数为b=15。
S1∪S2={11,13,15, 16,17,18,19,20,28,40}
两个序列的中位数在[15,20]范围内
（3）重复第（2）步，直到两个序列都只有一个元素时，取两者较小者。

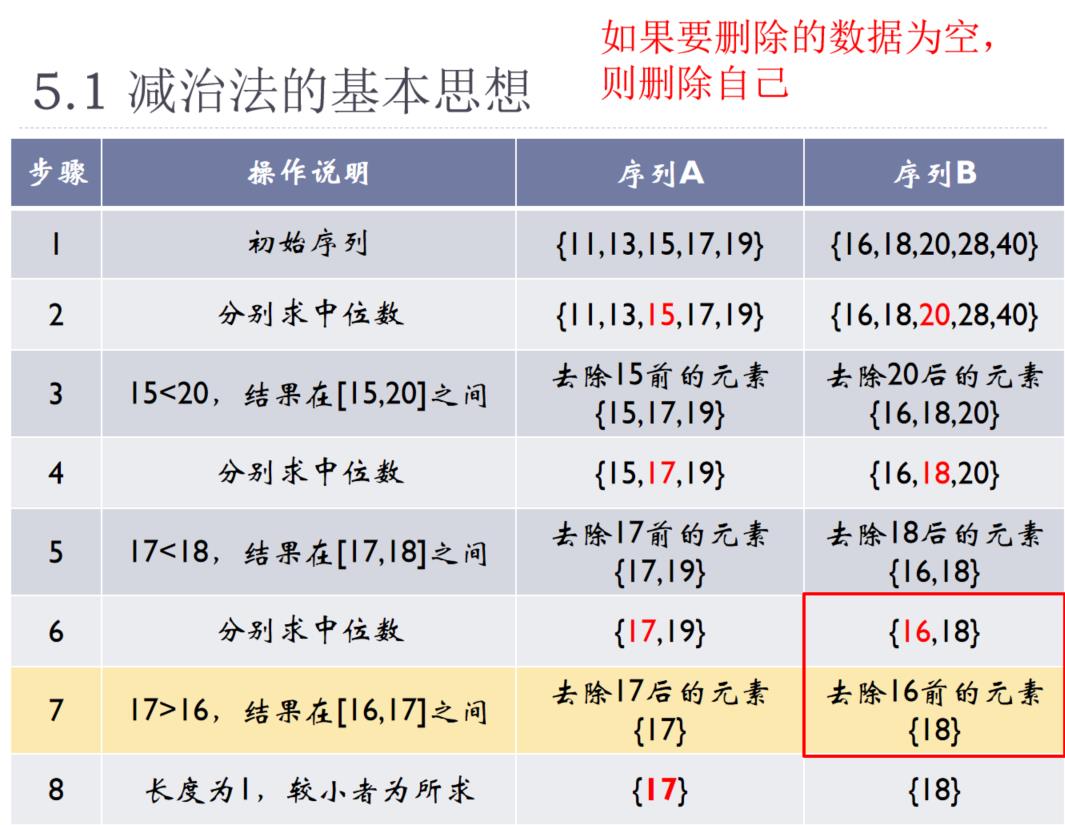
减治法的体现在于，每次求解，问题的规模都减少一半，而原问题的解就在这一半的子问题中

假如两个序列长度为n，每次迭代减少一半，一共经过log2n次后，序列长度变为1。每次迭代的任务是计算中位数位置，然后重置序列的开始和结束位置，均为O(1)

因此，其时间复杂度为O(log2n)。

5.1、折半查找

在有一个有序序列中查找值为k的记录。若查找成功，返回记录k所在的位置，否则，返回失败信息
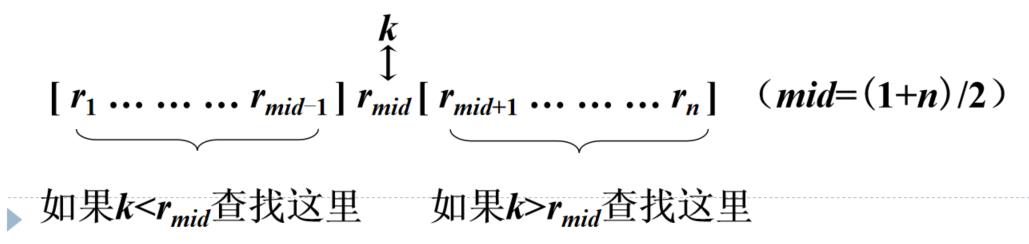
想法： 将待查找的数k与序列的中位数mid进行比较：
① 若k = rmid，返回结果；
② 若k < rmid，表明k在rmid往前的半段子序列中，下一步在前半段中寻找k；
③ 若k > rmid，表明k在rmid往后的半段子序列中，下一步在后半段中寻找k

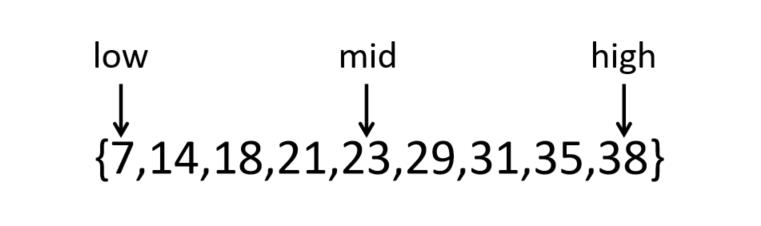
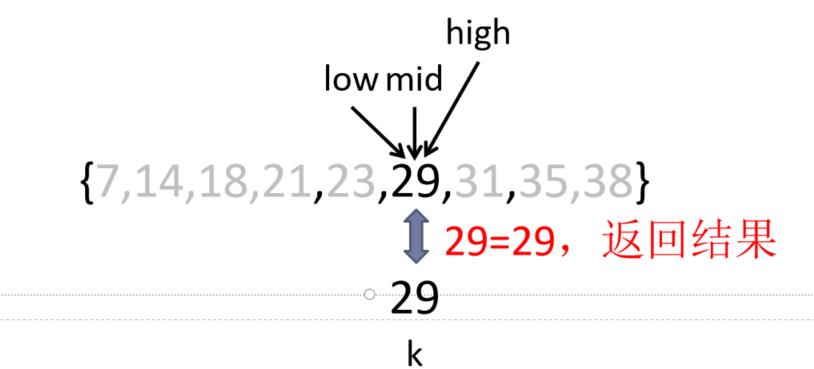
例：采用折半查找法在以下有序序列中查找29的过程
{7,14,18,21,23,29,31,35,38}
解：
①k= 29, low=0, high=8,mid=(low+high)/2=4
k与rmid比较；k>rmid；取mid往后的后半段；
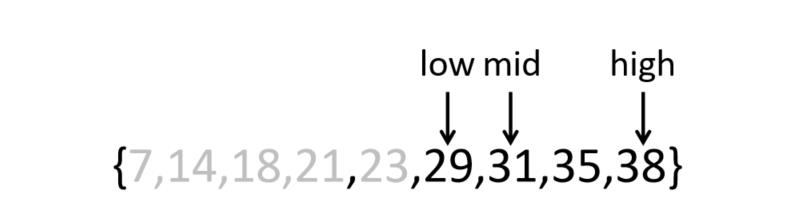
②k= 29, low=5, high=8,mid=(low+high)/2=6；
k与rmid比较；k<rmid;取mid往前的前半段。
③k= 29, low=5, high=5,mid=(low+high)/2=5
k与rmid比较，k=rmid；返回结果

时间复杂度分析
① 最好情况：序列中值即为待查找的数，比较1次
② 最坏情况：待查找的数需要一直折半，直到最后折半后的区域只乘一个元素时，才是待查找数或者也不是查找数。此时共比较的次数为折半的次数，为⌈log2n⌉
③ 平均情况
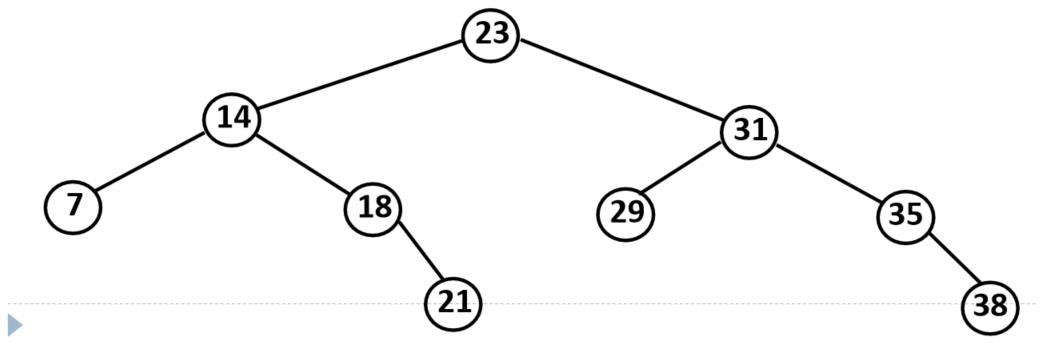
假设待查找的数是下列树结点中的其中一个，则可能的情况有n种，故pi = 1 / n；
若待查找的数是第i个结点，则若比较的次数为其在树中的层数。

5.2、二叉查找树

定义：二叉查找树是具有以下性质的二叉树：
① 若它的左子树不空，则左子树上所有结点的值均小于根结点的值；
② 若它的右子树不空，则右子树上所有结点的值均大于根结点的值；
③ 它的左右子树也是二叉排序树

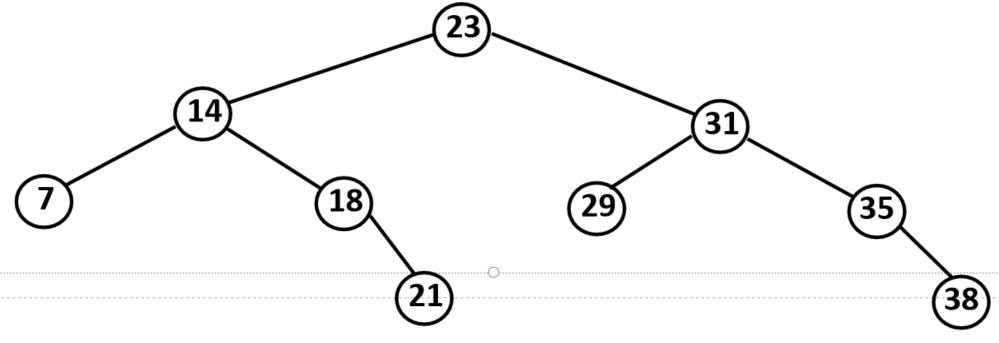
二叉查找树的建立——根据二叉查找树的定义来建立，依次对输入的数据建立查找树


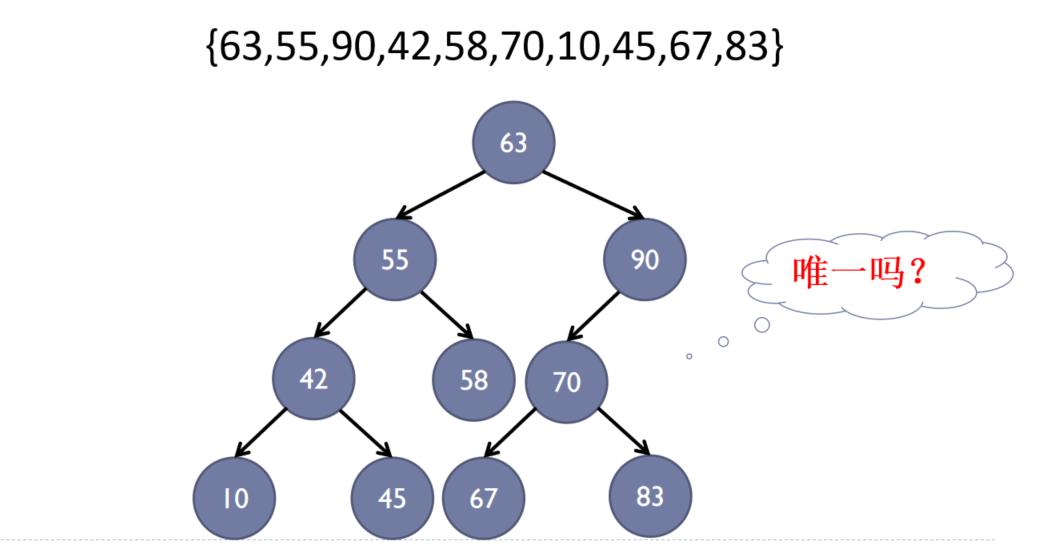
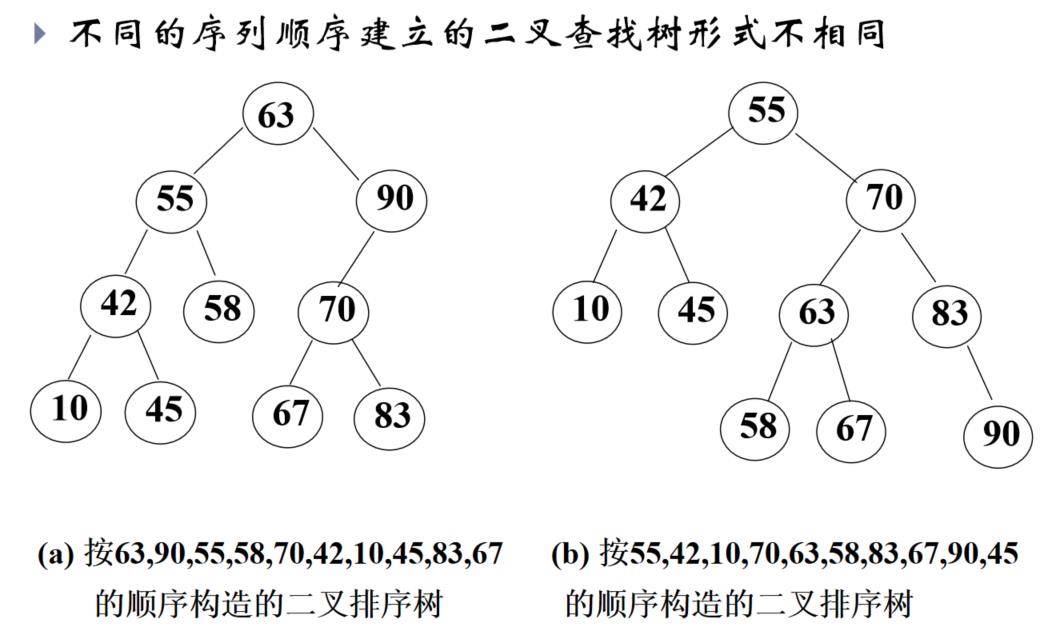
基于二叉查找树的查找算法：
（1）若root是空树，则查找失败；
（2）k=根结点的值，则查找成功；
（3）若k<根结点的值，则在root的左子树上查找；
（4）若k>根结点的值，则在root的右子树上查找。

在下面二叉查找树上查找83
① 跟根结点(63)比较，得到83>63，因此向右子树移动
② 跟结点(90)比较，得到83<90，因此向左子树移动
③ 跟结点(70)比较，得到83>70，因此向右子树移动
④ 跟结点(83)比较，得到83=83，查找成功

时间复杂度
查找所比较的次数实质上是二叉查找树从根结点到待查数所在结点的路径长度
① 最好情况：根结点即为待查找的数，比较1次；
② 最坏情况：与查找树的建立方式有关：
若建立查找树时以正序的方式输八，则查找树最深深度为n，而待查找数为序列的最后一个数，此时比较次数最多，为n
若查找树刚好能建立成完全二叉树，则树的最深深度为log2n
因此，最坏情况的时间复杂度在O(log2n)和O(n)之间

5.3、选择问题

问题： 设无序序列 T =(r1, r2, …, rn)，T的第k(1≤k≤n)小元素定义为T按升序排列后在第k个位置上的元素。给定一个序列T和一个整数k，寻找T的第k小元素的问题称为选择问题。特别地，将寻找第n/2小元素的问题称为中值问题。
想法：
（1）升序排序后直接读取第k个元素。采用最快的排序算法(归并排序)，其时间复杂度为O(nlog2n)
（2）采用减治法可把平均复杂度降低为O(n)：利用快速排序的划分过程
采用减治法求解选择问题的步骤：
（1）采用快速排序中的划分操作将无序序列分成两个子列，其中，轴值左侧子序列均比轴值小，轴值右侧子序列均比轴值大
（2）划分后，轴值所在的位置i实质上是轴值在序列按升序排序后所在的位置，即第i小。
（3）比较k和i：
① k=i, 表示ri即为要查找的数，返回；
② k<i, 表明要查的数比ri小，则递归在左侧子序列找第k小；
③ k>i, 表明要查的数比ri大，则递归找右侧子序列找第k小。

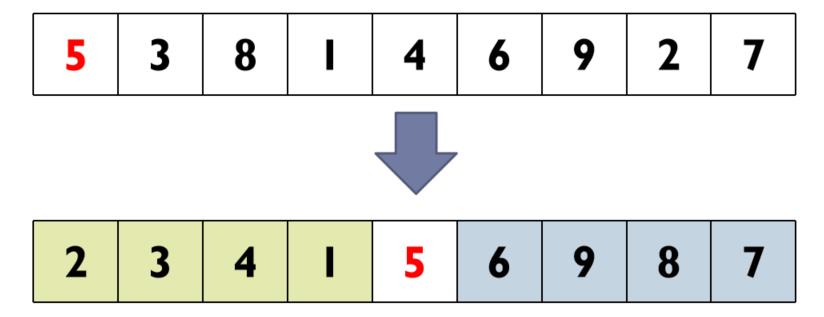
例： 采用减治法在序列{5,3,8,1,4,6,9,2,7}中查找第3小的过程
① 选择5为轴值，对序列进行第一次划分

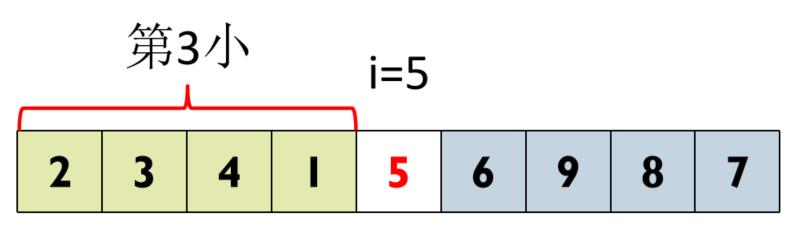
② 5是序列第5小元素，由于3<5，表明第3小元素在序列左侧子序列中

③ 选择2为轴值，对左侧子序列进行第二次划分

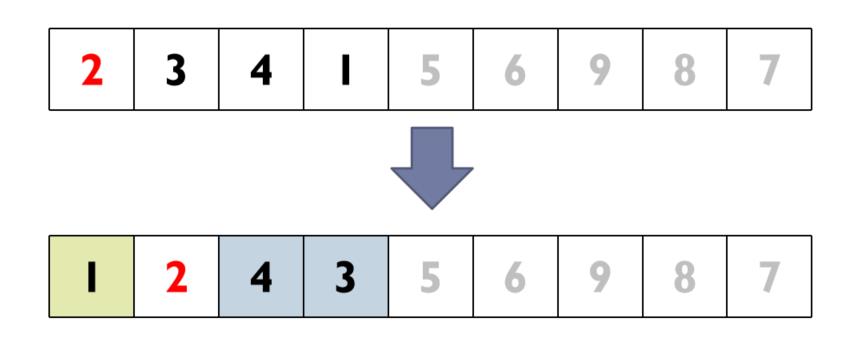
④ 2为序列第2小元素，由于2<3，表明第3小元素在右侧子序列中

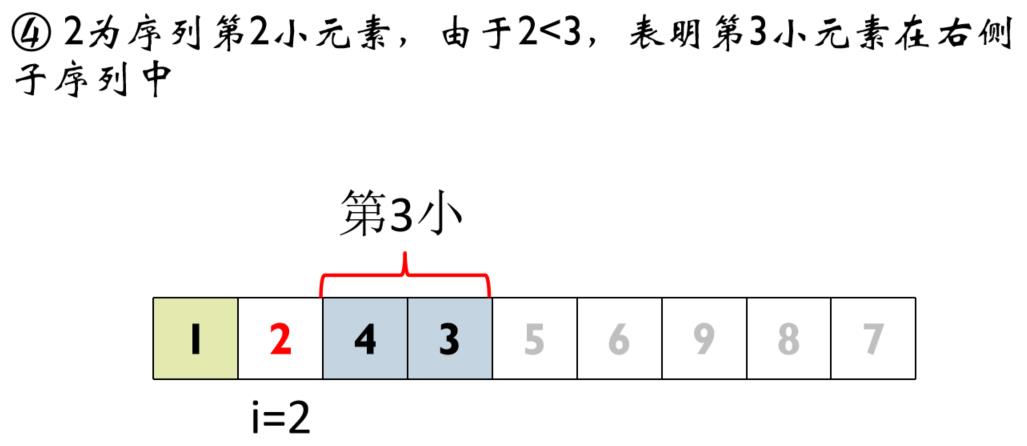
⑤ 选择4为轴值，对右侧子序列进行第三次划分

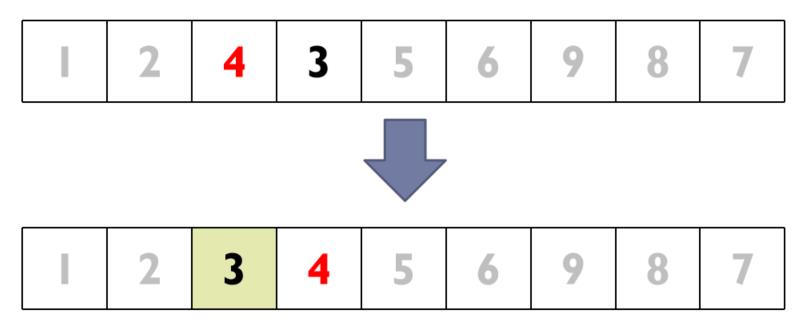
⑥ 4为序列第4小元素，由于3<4，表明第3小元素在其左侧子序列中

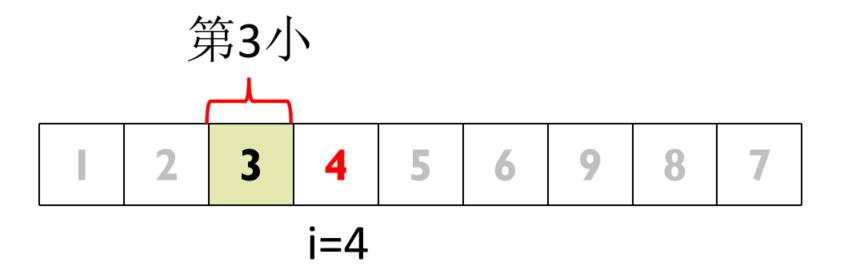
⑦ 选择3为轴值，对子序列进行第四次划分。由于序列中只有一个元素，则其即为第3小元素

5.4、排序问题

5.4.1、插入排序

基本思想： 依次将待排记录插入到有序区适当位置，直到全部记录插入完毕
基本思想（考虑升序排序情况）：
（1）将序列划分为有序区和无序区。有序区为序列第一个元素，无序区为剩下的元素。
（2）每一次操作都将无序区的第一个元素ri与有序区里从最后一个元素开始向前比较，直到找到第一个比ri小的元素rj，并将ri插入到rj后面；如果找不到元素比ri小，则ri要插入的位置为序列首部
（3）将ri插到rj后面，调整有序区中其它元素位置
插入排序的算法策略是减一法，即每插入一个元素后，原问题规模变成少了一个元素的子问题

例题：
对数据43,32,18,26,21,4,12,7,10,12进行插入排序，写出每趟的结果，并写出比较次数
注意：若当前数据插入到有序区最开头，与哨兵值也要比较1次

初始： (43) 32,18,26,21,4,12,7,10,12
第一趟： (32,43) 18,26,21,4,12,7,10,12 插32比较2次
第二趟： (18,32,43) 26,21,4,12,7,10,12 插18比较3次
第三趟： (18,26,32,43) 21,4,12,7,10,12 插26比较3次
第四趟： (18,21,26,32,43) 4,12,7,10,12 插21比较4次
第五趟： (4,18,21,26,32,43) 12,7,10,12 插4比较6次
第六趟： (4,12,18,21,26,32,43) 7,10,12 插12比较6次
第七趟： (4,7,12,18,21,26,32,43) 10,12 插7比较7次
第八趟： (4,7,10,12,18,21,26,32,43) 12 插10比较7次
第九趟： (4,7,10,12,12,18,21,26,32,43) 插12比较6次
共44次

5.4.2、堆排序

问题：采用堆结构来描述数据，并在此基础上实现排序
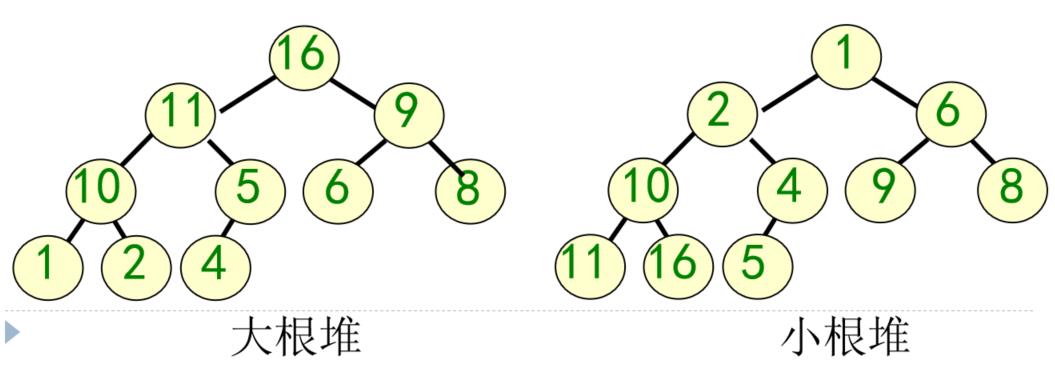
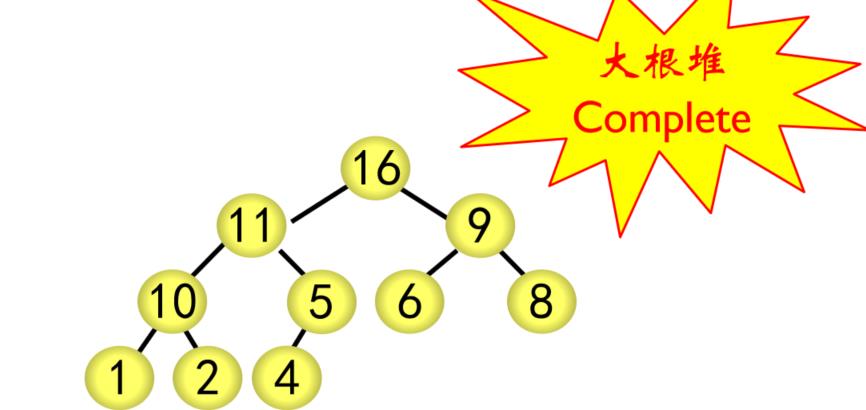
定义：堆——具有以下性质的完全二叉树：
每个结点的值都小于或等于左右孩子结点的值（小根堆）；或者每个结点的值都大于或等于其左右孩子结点的值（大根堆）。

基本思想：
（1）根据堆的特性，将待排序序列建立堆。升序排序采用大根堆；降序排序采用小根堆
（2）堆顶元素为最大值（大根堆）或最小值（小根堆），将该元素与最后一个元素交换并移入有序区
（3）调整无序区为一个堆结构
（4）重复（2）和（3）直到无序区剩一个元素
由于每次交换堆顶元素并调整堆后，无序区都是比原问题少一个元素的堆，因此堆排序也是采用减一法的设计策略
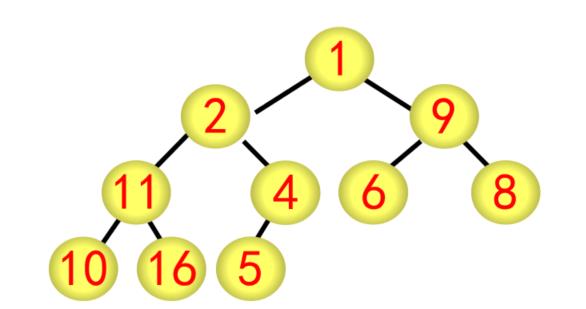
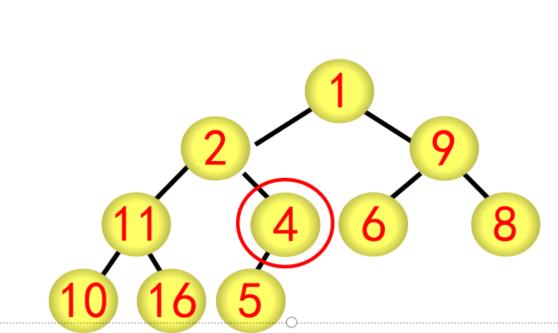
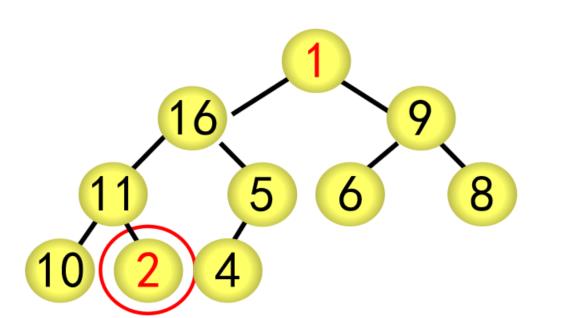
基本步骤（以序列{1,2,9,11,4,6,8,10,16,5}为例）
（1）建立堆
① 按广度优先方式建立完全二叉树，每个结点的编号按广度优先分配，如根结点为1号，最后的结点(5)为10号

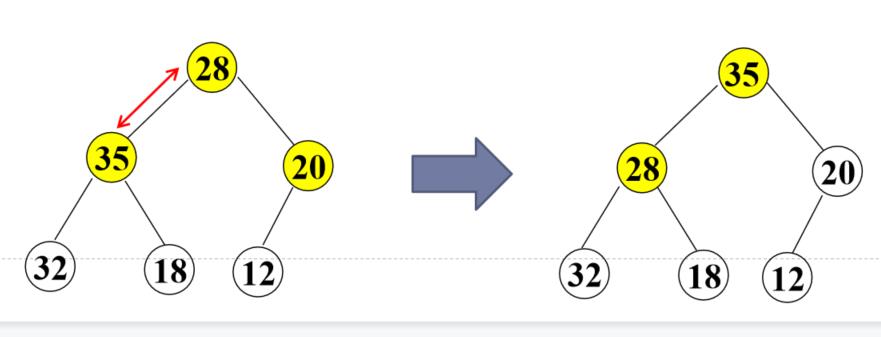
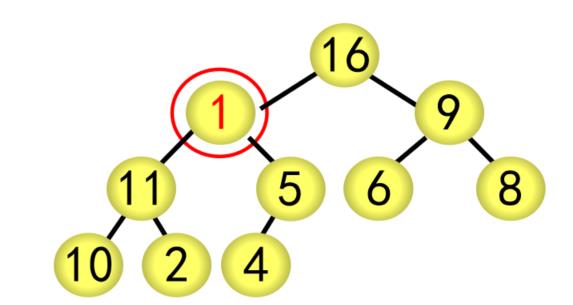
② 采用筛选法调整为大根堆
对当前结点(28)，若左右子树不全为空，则与左右子树的根结点比较，将较大者移为当前结点
对移动后的结点(28)，若左右子树不全为空，继续进行上述调整，直到该结点(28)的左右子树均为空


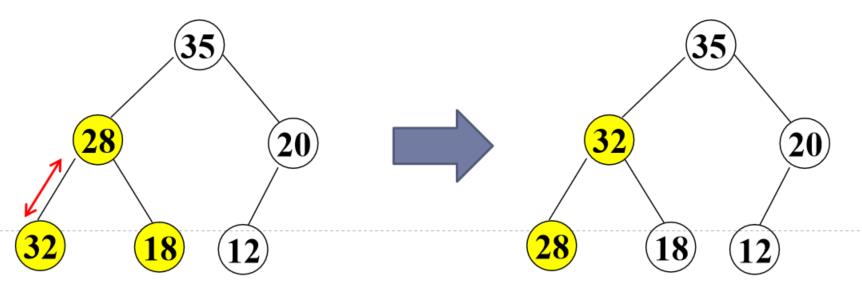
② 采用筛选法调整为大根堆，从编号为[n/2]5的结点开始往前调整








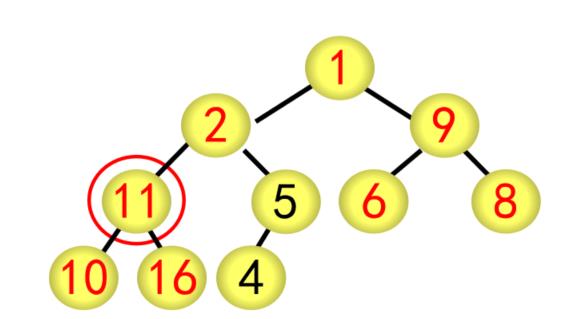
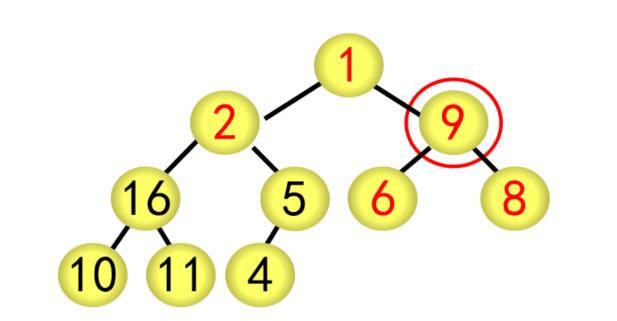
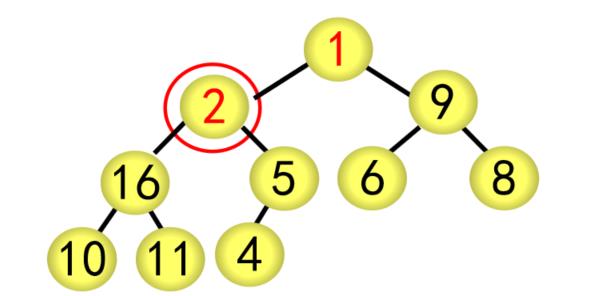
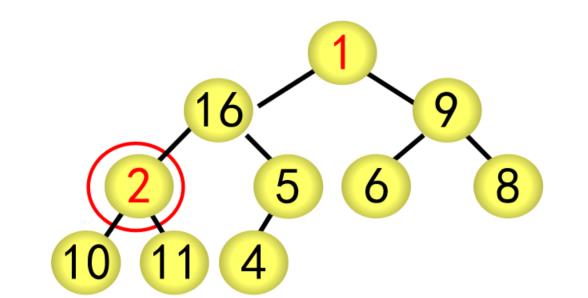
（2）交换
建立好大根堆后，堆顶元素即为最大值，将堆顶元素与最后的元素进行交换

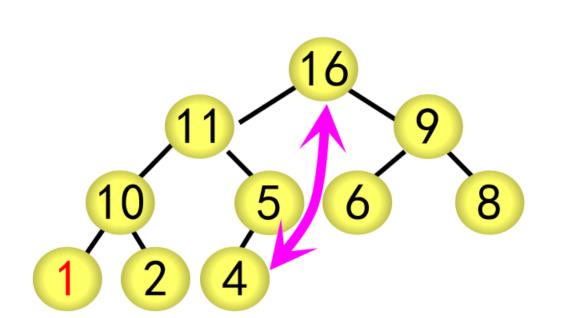
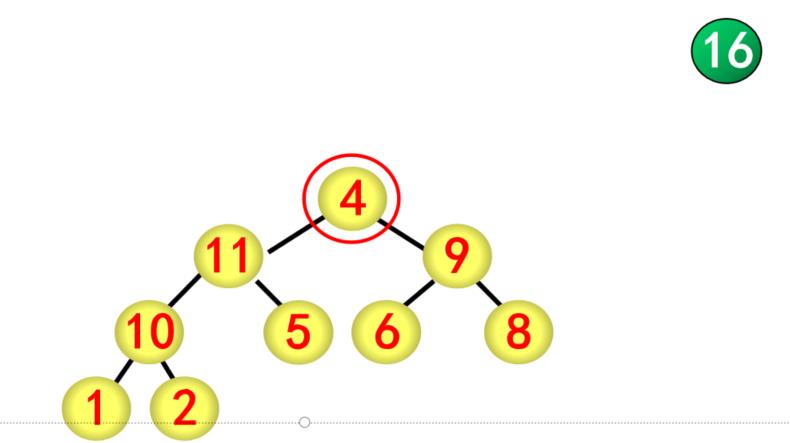
（3）调整堆
采用筛选法对根结点进行调整

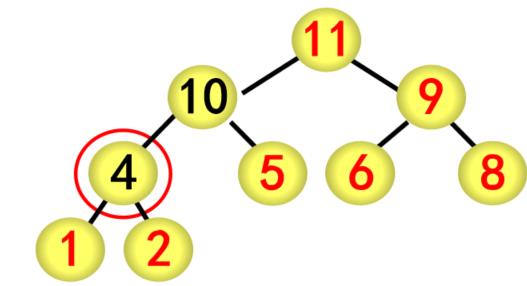
（4）重复交换与调整

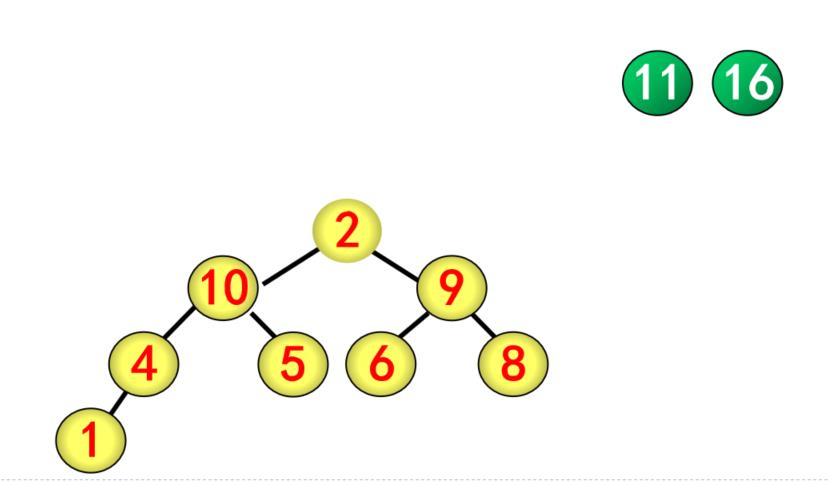
5.5、组合问题

5.5.1、淘汰赛冠军问题

淘汰赛：两队进行比赛，赢的一方继续下一场比赛；输的一方不得参加后面的比赛
（1）分治法思路：将选手分成2组（划分），分别决出两组各自的胜者（求解子问题），然后最后两组胜者再进行一次决赛（合并）。

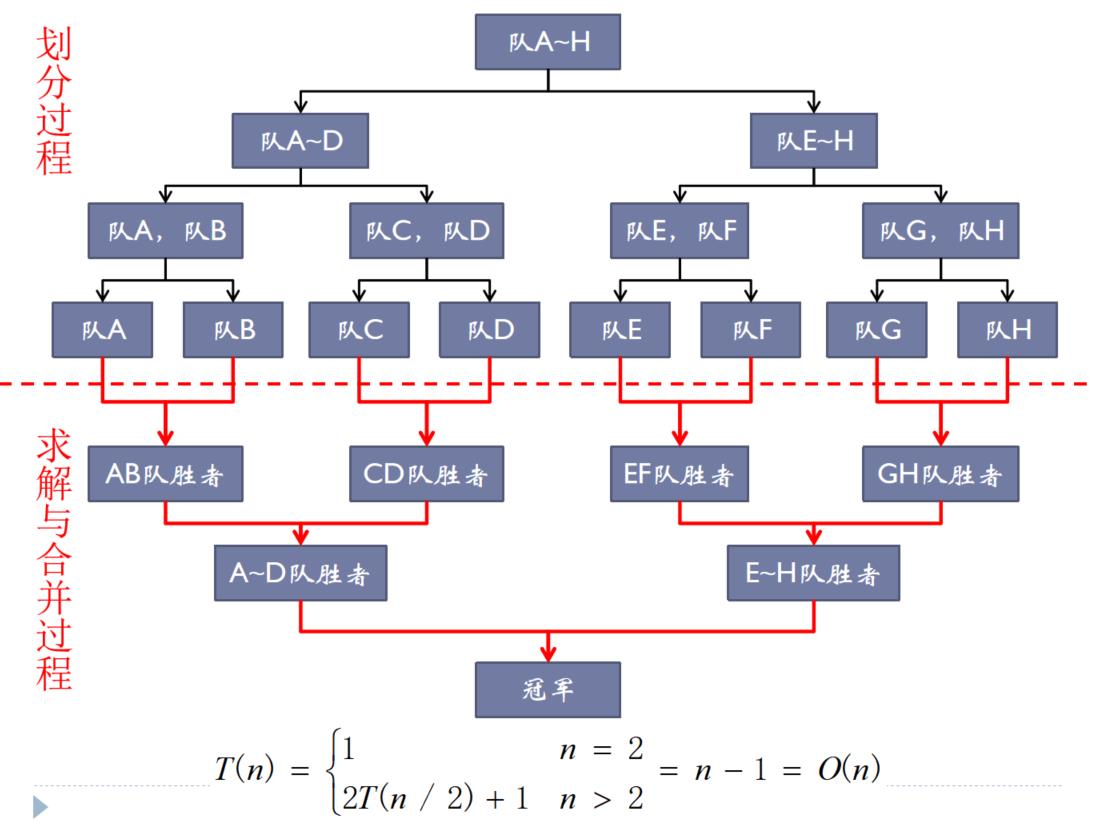
（2）减治

以上是关于数据结构与算法概念与理解（更新中）的主要内容，如果未能解决你的问题，请参考以下文章

CNN卷积概念理解

算法常识——结构与复杂度

通过动画轻松理解递归与动态规划

看动画轻松理解“递归”与“动态规划”

经典书数据结构与算法C++，第二版，738页pdf

看动画轻松理解「递归」与「动态规划」