[数据结构] 时间复杂度与空间复杂度

Posted 2021-06-09 哦哦呵呵

1. 算法效率如何确定

  算法的效率我们一般通过时间复杂度与空间复杂度两个方面一起来界定。时间复杂度来确定算法执行所需要的时间，空间复杂度用来确定该算法所需要的空间大小。

2. 时间复杂度

  时间复杂度怎么表示：基本语句的总执行次数就为时间复杂度，一般关注算法的最坏运行情况。通过大O渐进表示法表示。
1.算法最坏情况：任意输入规模的最大运行次数(上界) 时间复杂度
2.算法平均情况：任意输入规模的期望运行次数
3.算法最好情况：任意输入规模的最小运行次数(下界)

推导大O阶方法：

1. 用常数1取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

下面通过代码示例，进行时间复杂度计算：

普通代码时间复杂度

代码一：

// 计算基本语句的执行总次数
// 时间复杂度为 O(N*N + 2*N + 10)
// 根据大O阶表示法，可以省去系数常数，只保留最高阶
// 所以时间复杂度为 O(N^2)
void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; ++i)
	{
		for (int j = 0; j < N; ++j)
		{
			++count;
		}
	}

	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}

	int M = 10;
	while (M--)
	{
		++count;
	}

	printf("%d\\n", count);
}

代码二：

// 时间复杂度为 O(N + M)
// 因为N M 无法确定，所以无法省去
void Func3(int N, int M)
{
	int count = 0;
	for (int k = 0; k < M; ++k)
	{
		++count;
	}
	for (int k = 0; k < N; ++k)
	{
		++count;
	}
	printf("%d\\n", count);
}

代码三：

// 时间复杂度为O(1)
// 参数N与函数内基础语句执行次数无关
void Func4(int N)
{
	int count = 0;
	for (int k = 0; k < 100; ++k)
	{
		++count;
	}
	printf("%d\\n", count);
}

代码四：

// 时间复杂度为 O(log2 n)
// 每次查找为上次长度的一半，所以可得公式为 2^M = N; (N为总长度，M为次数)
// 所以 M = log2 N
int BinarySearch(int* a, int n, int x)
{
	assert(a);
	int begin = 0;
	int end = n - 1;

	while (begin < end)
	{
		int mid = begin + ((end - begin) >> 1);
		if (a[mid] < x)
			begin = mid + 1;
		else if (a[mid] > x)
			end = mid;
		else
			return mid;
	}

	return -1;
}

递归时间复杂度

递归时间复杂度 = 单次递归次数 * 总的递归次数

代码一：

// 时间复杂度 O(N)
long long Factorial(size_t N)
{
	return N < 2 ? N : Factorial(N - 1) * N;
}

  图示：N=5为例

代码二：

// 时间复杂度 O(2^N)
// 根据图可以看出是一颗二叉树，并且每一层递归次数为等差数列 公差为2 所以时间复杂度按照等差数列计算
long long Fibonacci(size_t N)
{
	return N < 2 ? N : Fibonacci(N - 1) + Fibonacci(N - 2);
}

  图示：N=5为例

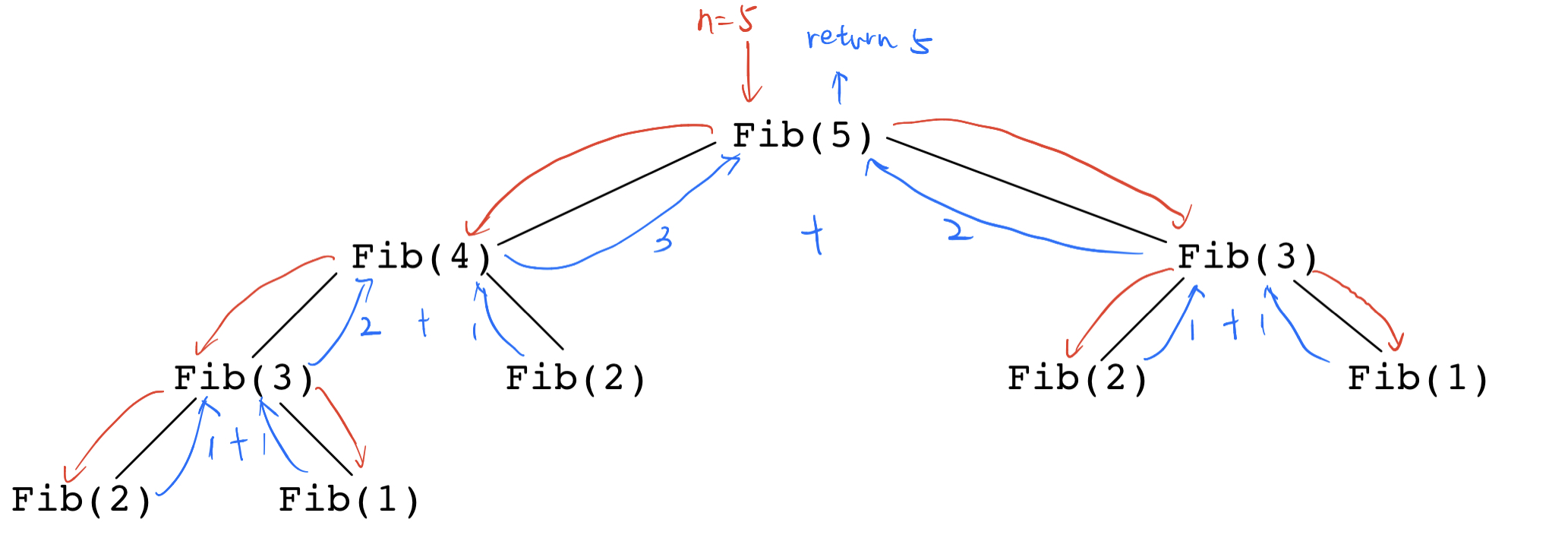
  从图片可以看出，每层递归调用次数为等差数列形式递增，所以可根据等差数列得出：1*(1-2^n) / (1-2)，根据大O阶可得出时间复杂度为O(2^N);
  可见，根据递归计算斐波那契数列时间复杂度非常之高，所以一般不适用递归计算斐波那契数列，而是使用迭代方法计算，可将时间复杂度降至 O(N)

3. 空间复杂度

  空间复杂度是在运行过程中临时占用空间的大小的密度，由于上述已经详细讲述了时间复杂度的算法，空间复杂度算法与上述基本相同。


代码一:

// 计算BubbleSort的空间复杂度？
// 因为没有使用额外空间 所以空间复杂度为 O(1)
void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

代码二：

// 因为循环中每次开辟一个长整型空间
// 所以空间复杂度为 O(N)
long long* Fibonacci(size_t n)
{
	if (n == 0)
		return NULL;

	long long* fibArray =
		(long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1; for (int i = 2; i <= n; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}

递归空间复杂度

递归空间复杂度 = 单次需要空间 * 递归深度

  递归每个函数执行时，都需要开辟一个栈帧，在整个递归调用过程中，栈帧最大累积了多少个就是空间复杂度。

代码一：

long long Factorial(size_t N)
{
 return N < 2 ? N : Factorial(N-1)*N;
}

由图可见，单次所需空间为1个栈帧，最大深度为5
图示: N=5

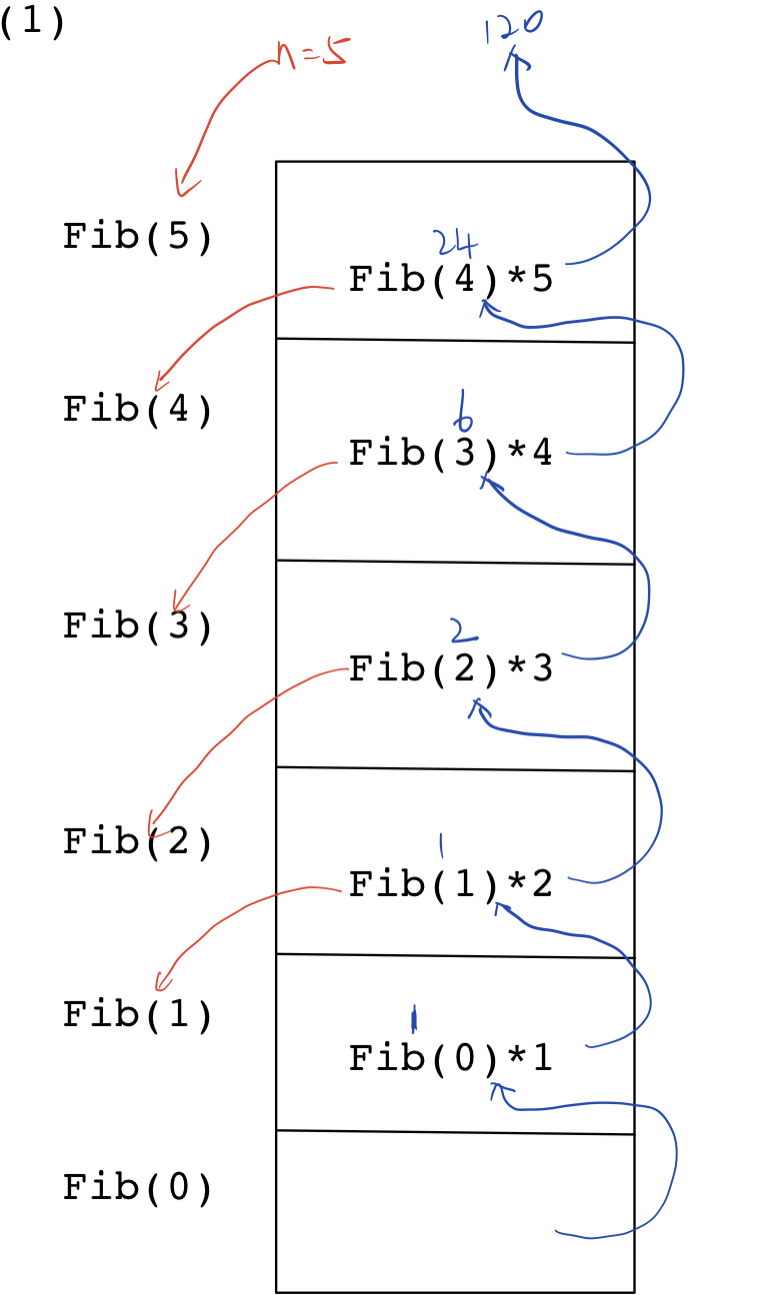
代码二：

// 空间复杂度 O(N)
long long Fibonacci(size_t N)
{
	return N < 2 ? N : Fibonacci(N - 1) + Fibonacci(N - 2);
}

斐波那契数列的递归空间复杂度为O(n)，因为在函数递归调用时，最大深度为N，并且计算顺序先计算左递归值，在进行右递归。在左递归返回时，就已经释放了栈帧空间，所以累计深度为 N个，所以复杂度为O(n)。

注意：栈空间有固定大小，函数递归深度不能太深。