[蓝桥杯]看一看,国二变国一,第十一届决赛B组试题解析
Posted @书生
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[蓝桥杯]看一看,国二变国一,第十一届决赛B组试题解析相关的知识,希望对你有一定的参考价值。
A 美丽的2
题目描述:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝特别喜欢 22,今年是公元 2020 年,他特别高兴。 他很好奇,在公元 1年到公元 2020年(包含)中,有多少个年份的数位中包含数字 22?
题解:
本题是比较简单的一道题,即让我们1~2020这些数字中,哪些数字上包含2,犹如范围较小,我们只需要循环遍历,就可以轻松的解决这个问题,代码如下:
代码
#include <iostream>
using namespace std;
int main()
{
// 请在此输入您的代码
int result=0;
for(int i=1;i<=2020;i++){
int num=i;
while(num){
if(num%10==2)
{
result+=1;
break;
}
num/=10;
}
}
cout<<result<<endl;
return 0;
}
题目链接:
https://www.lanqiao.cn/problems/1018/learning/
B 扩散
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝在一张无限大的特殊画布上作画。
这张画布可以看成一个方格图,每个格子可以用一个二维的整数坐标表示。
小蓝在画布上首先点了一下几个点:(0,0),(2020,11),(11,14),(2000,2000)。
只有这几个格子上有黑色,其它位置都是白色的。
每过一分钟,黑色就会扩散一点。具体的,如果一个格子里面是黑色,它就会扩散到上、下、左、右四个相邻的格子中,使得这四个格子也变成黑色(如果原来就是黑色,则还是黑色)。
请问,经过 2020 分钟后,画布上有多少个格子是黑色的。
题解:
在这道题中,我们需要注意 扩散的方向是垂直方向即(上下左右),且每过一分钟就会扩散一个距离,题目要求2020分钟之后,即在单个方向上,扩散的距离为2020,即使题目上说坐标是无限大的,但是由于条件限制,我们是可以模拟出坐标的:
四个点经过2020分钟的扩散,情况如下
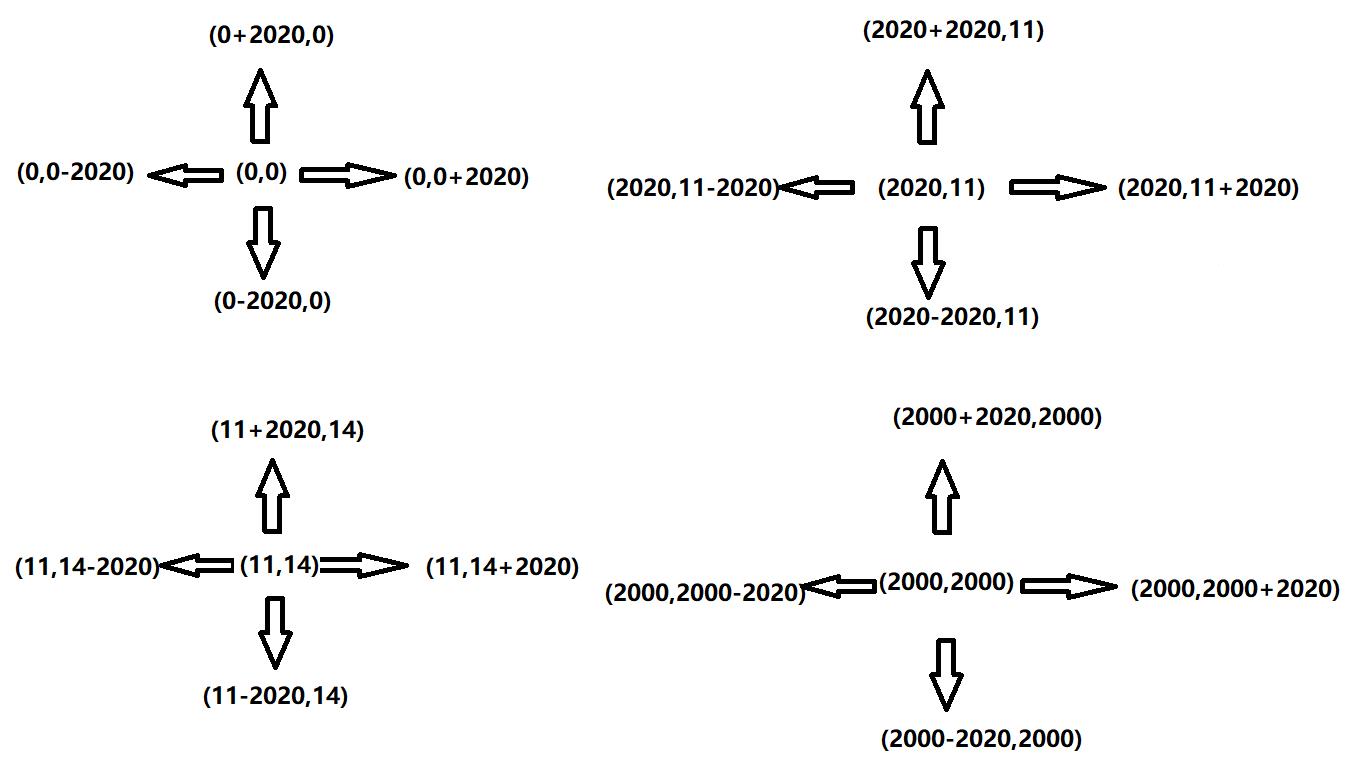
通过上面的扩散情况,我们发现坐标的范围其实在 x轴属于(0-2020,2000+2020) , y轴属于(0-2020,2020+2020)
我们仅仅需要用一个二位数组表示坐标系(未扩散到的地方用0表示,扩散到的地方用1标识),每过一分钟,从四个点的位置处扩散,2020分钟扩散完毕之后,判断二维数组中1的个数即可
代码:
#include<iostream>
#include<queue>
using namespace std;
struct node{
node(int _x,int _y,int _cnt)
:x(_x)
,y(_y)
,cnt(_cnt)
{
}
int x , y , cnt;
//cnt记录本次移动是第几次移动
};
//因为有的编程语言中数组坐标不支持负数,所以我们整体加上2020
int nex[4][2] = {{1 , 0} , {-1 , 0} , {0 , 1} , {0 , -1}};
const int row=2020+2020+2020+1;
const int col=2000+2020+2020+1;
const int B = 2020;
int map[row][col];
int bfs()
{
queue<node> que;
int cnt = 4; // 初始的黑色的点的个数
//我们需要使用队列来记录我们需要从那个点进行方向移动
que.push(node(0 + B , 0 + B , 0));
que.push(node(2020 + B , 11 + B , 0));
que.push(node(2000 + B , 2000 + B , 0));
que.push(node(11 + B , 14 + B , 0));
map[0 + B][0 + B] = 1;
map[2020 + B][11 + B] = 1;
map[2000 + B][2000 + B] = 1;
map[11 + B][14 + B] = 1;
while(!que.empty())
{
node u = que.front();
que.pop();
//移动次数为2020时,表示我们已经移动了2020分钟,则可以停止扩散了
if(u.cnt == 2020) continue ;
for(int i = 0 ; i < 4 ; i ++)
{
int tx = u.x + nex[i][0] , ty = u.y + nex[i][1];
if(map[tx][ty]) continue ;
cnt ++ ;
map[tx][ty] = 1;
que.push(node(tx , ty , u.cnt + 1));
}
}
return cnt;
}
int main()
{
cout << bfs() << '\\n';
return 0;
}
题目链接:
https://www.lanqiao.cn/problems/1019/learning/
C 阶乘约数
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
定义阶乘 n! = 1 × 2 × 3 × · · · × n
请问 100!(100 的阶乘)有多少个正约数。
题解:
所谓的正约数,就是指约数是一个整数。
本题的暴力解:先求出100!,然后进行1~100!循环遍历,判断每个数是否是100!的约数即(100! % i==0) ,然而不幸的是100! 是非常大的,即使我们使用long long也存储不下,因此暴力解是无法实现的!
但是我们可以采用其他的方法,唯一分解定理进行求解;
什么是唯一分解定理,我们先不去理会。首先我们达成一个共识:一个数必定由n个质数相乘得到(质数仅有1和它本身相乘,而合数可以分解称若干个质数相乘,如4=2*2 ,因此任何数都可以分解成若干个质数相乘)
那这个与我们这道题有什么关系呢?
我们以5!为例 5!=5* 4 * 3 * 2 可以分解为5! =5 * ( 2 * 2)* 3 * 2
而唯一约数定理的内容

也就是说5!=2^3 * 3^1 * 5^1 ; 2,3,5就是p1,p2,p3即质数;其对应的指数a1,a2,a3就是3,1,1

再根据约束个数定理:我们将 指数+1 再全部相乘就可以得到我们想要的结果。
2^3 的约数为1 2 4 8
3^1 的约数为1 3
5^1 的约数为1 5
这些约数再次相乘又会得到其他的约数,这就是约数个数定理;
我们采用暴力方法来确认依靠两个定理解题是否正确,根据定理解的5!的约数个数为16 ,与暴力解的结果相同
暴力解验证:
int main(){
int result=0;
int num=1;
for(int i=1;i<=5;++i)
{
num*=i;
}
for(int i=1;i<=num;i++){
if(num%i==0)
{
cout<<i<<endl;
result++;
}
}
cout<<"result:"<<result<<endl;
return 0;
}

代码:
#include <iostream>
using namespace std;
int main(){
long long result=1;
int arr[101]={0}; //用来存储质数的指数 ,100以内数的约数不会超过100,故去数组大小为101
for(int i=1;i<=100;i++){
int tmp=i;
for(int j=2;j*j<=tmp;j++){
if(tmp%j==0){
//如果找到约数,一直相除,就可以得到此约数的指数,这个约数一定是质数
//因为质数2,3在前面即使此处j=4或6,一定取余不为0,在前面已经被分解了
while(tmp%j==0){
tmp/=j;
arr[j]++;
}
}
}
if(tmp>1)
{
//设置该if语句的原因 eg:2 2*2>2 ;进不去上面的for循环,我们需要再次判断,以防遗漏
//cout<<"i"<<i<<"tmp"<<tmp<<endl;
arr[tmp]++;
}
}
for(int i=0;i<101;i++){
if(arr[i]!=0)
result*=(arr[i]+1);
}
cout<<result<<endl;
return 0;
}
题目链接:
https://www.lanqiao.cn/problems/1020/learning/
D 本质上升序列
题目描述:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。 小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个? 例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
题解:
动态规划
dp[i] 表示前i个字符构成上升序列的个数
如果我们遍历到第j个字符,我们由两种选择:
1不将其加入上升序列,那么dp[j] =dp[j-1]
2将其加入上升序列,要构成上升序列,我们要找str[j]之前的字符,显然使用一维数组是无法满足我们解题需要的,因此我们重新构建二维数组
dp[ i ][ 26 ] 表示前i个字符以a+[0,26)字符结尾的上升序列的个数
如果我们遍历到第j个字符c,我们由两种选择:
1不将其加入上升序列,那么dp[j][c] =dp[j-1][c]
2将其加入上升序列,要构成上升序列,我们要找c之前的字符
for(int k=0;k<c-'a';k++){
dp[j][c]+=dp[j-1][k];
}
因为要构成本质不同的序列,我们需要知道前面最近的一个相同字符的位置
因此构造一个last数组,保存其位置;
代码:
#include <iostream>
#include<vector>
using namespace std;
int main(){
//给字符串前面增加一个空格,使得dp数组的含义容易理解
string str=" tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
//字符串的大小
int size=str.size();
//cout<<"size"<<size<<endl;
//前面一个最近相同字母的位置
vector<int> last(26,0);
//动态规划数组 ,表示前i个字符,以‘a’+j字符结尾构成上升序列的个数
vector<vector<int> > dp(size,vector<int>(26,0));
for(int i=1;i<size;i++){
//直接舍弃第i个字符加入上升序列
for(int j=0;j<26;j++){
dp[i][j]=dp[i-1][j];
}
//将第i个字符加入上升子序列
//单独的一个元素可以作为一个上升子序列
dp[i][str[i]-'a']++;
//倘若当前字符为c ,我们需要找前面以a或者b结尾的字符,
//以此构成递增序列
for(int j=0;j<str[i]-'a';j++){
dp[i][str[i]-'a']+=dp[i-1][j];
}
//因为题目要求构成本质不同的序列,我们需要找到上一次字符,
//减去上一次字符对应的次数
//(ablb) ab由两种情况前两个字符构成ab
//第二种跳过第二个第三个字符与第四个字符构成b
//由于要求本质不同的上升序列,我们需要减去重复的情况
dp[i][str[i]-'a']-= dp[last[str[i]-'a']][str[i]-'a'];
//更新字符的位置
last[str[i]-'a']=i;
}
long long result=0;
for(int i=0;i<26;i++){
result+=dp[size-1][i];
}
cout<<result<<endl;
return 0;
}
题目链接:
https://www.lanqiao.cn/problems/1021/learning/
E 玩具蛇
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝有一条玩具蛇,一共有 16节,上面标着数字 1至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
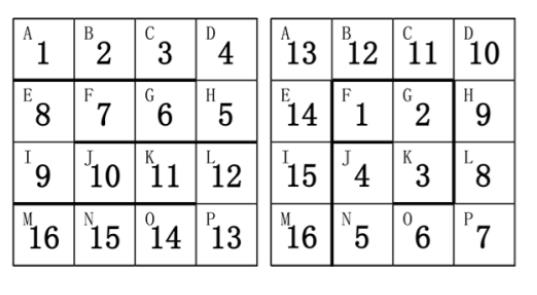
请帮小蓝计算一下,总共有多少种不同的方案。如果两个方案中,存在玩具蛇的某一节放在了盒子的不同格子里,则认为是不同的方案。
题解:
这道目的话,其实考察的是dfs算法,也可以认为是回溯算法:
也许你并不了解这算法,但是实现很简单:
- 我们需要设定一个起点
- 从起点选择一个方向(上下左右)进行移动
- 继续执行步骤2,直到我们把整个4*4方盒全部放满后,就是一种存放方案
代码:
#include <iostream>
#include<vector>
using namespace std;
//某个位置放有字符0,表示可以放置字符
vector<vector<char> > vv(4,vector<char>(4,'0'));
int dir[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
void dfs(int row,int col,int count,int& result){
//我们将16个字符全部防止完毕之后,构成一种方法
if(count>=16){
result++;
return;
}
//选择四个方向中的一个方向移动
for(int i=0;i<4;i++){
int x=row+dir[i][0];
int y=col+dir[i][1];
//判断移动后的位置是否合理,越界不合理,我们不能移动;
//要移动的位置如果已经存放过东西,也不合理,不进行移动
if(x<0||x>=4||y<0||y>=4){
continue;
}
if(vv[x][y]!='0'){
continue;
}
//存放我们要防止的字符
vv[row][col]=count+'0';
dfs(x,y,count+1,result);
//上一次方法完毕,将该位置字符清除
vv[row][col]='0';
}
}
int main(){
int result=0;
for(int i=0;i<4;i++){
for(int j=0;j<4;j++){
//利用双重循环,使得方盒每个位置都可以设置为起点
dfs(i,j,1,result);
}
}
cout<<result<<endl;
return 0;
}
题目链接:
https://www.lanqiao.cn/problems/1022/learning/
注:如果本篇博客有任何错误和建议,欢迎伙伴们留言,你快说句话啊!
部分参考《蓝桥云课》,如有侵权请及时联系!
如有帮助,希望伙伴可以点赞+收藏!
👇 👇
点赞 收藏
以上是关于[蓝桥杯]看一看,国二变国一,第十一届决赛B组试题解析的主要内容,如果未能解决你的问题,请参考以下文章