线索二叉树详解

Posted 2021-06-09 即刻笔记CS

1 由来

当用二叉链表作为二叉树的存储结构时，可以很方便地找到某个节点的左右孩子；但一般情况下，无法直接找到该节点在某种遍历序列中的前驱和后继节点。

如何寻找特定遍历序列中二叉树节点的前驱和后继？

解决的方法：

• 通过遍历寻找（土方法）——费时间（设立指针在遍历是始终指向访问结点的前驱）
• 利用二叉链表中的空指针域（线索二叉树）。

线索二叉树的节点结构

2 用土方法找到中序前驱

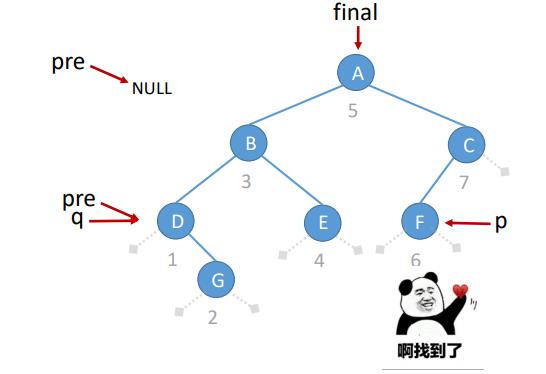
//中序遍历
void FindPre(BiTree T){
 if(T!=ULL){
        FindPre(T->lchild);
        visit(T);
        FindPre(T->rchild);
    }
}
//访问结点q
void visit(BiTNode *q){
 if(q==p)   //当前访问结点刚好是p
        final = pre;  //找到p的前驱
    else
        pre = q;    //pre指向当前访问的节点
}
//辅助全局变量，用于查找节点p的前驱
BiTNode *p;    //p指向目标节点
BiTNode * pre=NULL;   //指向当前访问节点的前驱
BiTNode * final=NULL;  //用于记录最终的结果

3 线索二叉树实现

    3.1 中序线索化

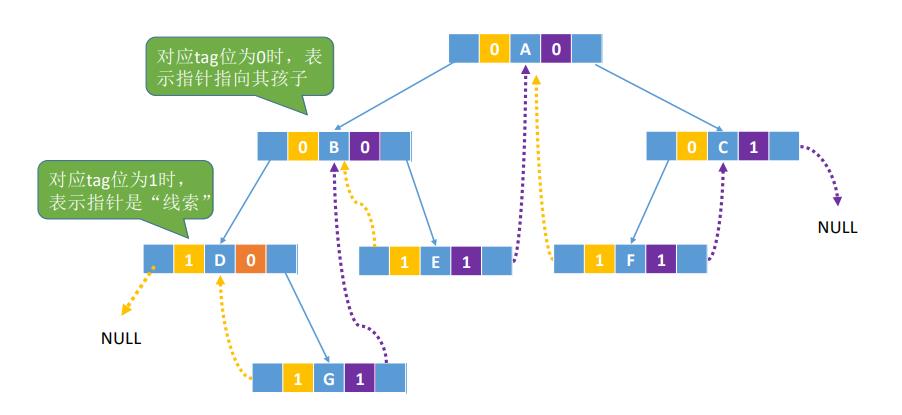
//全局变量 pre ，指向当期访问节点的前驱
ThreadNode *pre=NULL;
//线索二叉树结点
typedef struct ThreadNode{
    int data;
    struct ThreadNode *lchild, *rchild;
    int ltag=0, rtag=0;//左右线索标志
}ThreadNode,*ThreadTree;
//中序遍历二叉树。一边遍历一边线索化
void InThread(ThreadTree T){
    if(T!=NULL){
        InThread(T->lchild);
        visit(T);
        InThread(T->rchild);
    }
}
//访问线索二叉树结点
void visit(ThreadTree q){
    if(q->lchild==nullptr){//左子树为空，建立前驱线索
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre!=nullptr&&pre->rchild==nullptr)
    {
        pre->rchild = q;//建立前驱结点的后继线索
        pre->rtag = 1;
    }
    pre = q;
}
//在经历上面InThread()遍历之后，除了最右下的节点都已经线索化了，所以还需将最右下节点的rtag更改为1；
//中序先线索化二叉树T
void CreatInThread(ThreadTree T){
    pre = nullptr;
    if(T!=nullptr){
        InThread(T);
        if (pre->rchild==nullptr)
            pre->rtag = 1;
    }
}

       3.2 先序线索化

//全局变量 pre，指向当前访问节点的前驱
ThreadNode *pre = NULL;
//先序遍历二叉树，一边遍历一边线索化
void PreThread(ThreaTree T){
    if(T!=NULL){
        visit(T);
        if(T->ltag == 0)//lchild不是前驱线索
            PreThread(T->lchild);
        PreThread(T->rchlid);
    }
}
void visit(ThreadNode *p){
    if(q->lchild == NULL){//左子树为空，建立前驱线索
  q->lchild = pre;
         q->ltag = 1;
    }
    if(pre!=NULL && pre->rchild == NULL){
        pre->rchild = q;//建立前驱结点的后继线索
        pre->rtag = 1;
    }
    pre = q;
}
//
void CreatPreThread(ThreadTree T){
 pre = NULL;  //pre初始化为NULL
    if(T!=NULL){  
        PreThread(T);
        if (pre->rchild == NULL)
            pre->rtag = 1;//处理最后一个节点
    }
}

    3.3 后序线索化

//全局变量 pre ，指向当期访问节点的前驱
ThreadNode *pre=NULL;
//后序遍历二叉树。一边遍历一边线索化
void PostThread(ThreadTree T){
    if(T!=NULL){
        PostThread(T->lchild);
        PostThread(T->rchild);
        visit(T);
    }
}
//访问线索二叉树结点
void visit(ThreadTree q){
    if(q->lchild==nullptr){//左子树为空，建立前驱线索
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre!=nullptr&&pre->rchild==nullptr)
    {
        pre->rchild = q;//建立前驱结点的后继线索
        pre->rtag = 1;
    }
    pre = q;
}
//在经历上面InThread()遍历之后，除了最右下的节点都已经线索化了，所以还需将最右下节点的rtag更改为1；
//后序先线索化二叉树T
void CreatInThread(ThreadTree T){
    pre = nullptr;
    if(T!=nullptr){
        PostThread(T);
        if (pre->rchild==nullptr)
            pre->rtag = 1;
    }
}

4 在线索二叉树中找前驱后继（以中序线索化为例）

*⭐⭐在中序线索二叉树中找到指定结点 p 的中序后继 next

①若 p->rtag==1 ，则 next = p->rchild

②若 p->rtag==0 ,

next = p 的右子树中最左下结点

//找到以P为根的子树中，第一个被中序遍历的节点
ThreadNode *Firstnode(ThreadNode *p){
    //循环找到最坐下节点（不一定是叶结点）
    while (p->ltag==0)
        p = p->lchild;
    return p;
}
//在中序线索二叉树中找到节点p的后继节点
ThreadNode *Nextnode(ThreadNode *p){
    //右子树中最左下节点
    if(p->rtag==0)
        return Firstnode(p->rchild);
    else
        return p->rchild;//rtag==1直接返回搜索
}
//对中序线索二叉树进行中序遍历（利用线索实现的非递归算法）
void Inorder(ThreadNode *T){
    for (ThreadNode *p = Firstnode(T); p != nullptr;p=Nextnode(p))
        visit(p);
}
//时间复杂度O(1)

*⭐⭐在中序线索二叉树中找到指定结点 p 的中序前驱 pre

①若 p->ltag==1 ，则 pre = p->lchild

②若 p->ltag==0

pre = p 的左子树中最右下结点

//找到以P为根的子树中，第一个被中序遍历的节点
ThreadNode *Lastnode(ThreadNode *p){
    //循环找到最坐下节点（不一定是叶结点）
    while (p->ltag==0)
        p = p->lchild;
    return p;
}
//在中序线索二叉树中找到节点p的前驱节点
ThreadNode *Prenode(ThreadNode *p){
    //右子树中最左下节点
    if(p->ltag==0)
        return Lastnode(p->lchild);
    else
        return p->lchild;//ltag==1直接返回搜索
}
//对中序线索二叉树进行中序遍历（利用线索实现的非递归算法）
void Inorder(ThreadNode *T){
    for (ThreadNode *p = Lastnode(T); p != nullptr;p=Prenode(p))
        visit(p);
}

（图片、代码来源于王道考研）