基于GMM-HMM的语音识别系统

Posted 栋次大次

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于GMM-HMM的语音识别系统相关的知识，希望对你有一定的参考价值。

目录

本文介绍GMM-HMM语音识别系统，虽然现在主流端到端系统，但是传统识别系统的学习是很有必要的。阅读本文前，需要了解语音特征提取、混合高斯模型GMM、隐马尔科夫模型HMM的基础知识（可以参考我的前几篇文章）。笔者能力有限，如有错误请指正！

GMM-HMM语音识别系统的框架：

  1. 数据准备：数据源准备(wav/txt)、其他数据(词典、音素集等)、验证集、测试集
  2. 特征提取：MFCC
  3. 单音素GMM-HMM训练：单音素为三音素提供对齐
  4. 三音素GMM-HMM训练
  5. 解码

语音识别的几个概念：

  • 对齐：音频和文本的对应关系
  • 训练：已知对齐，迭代计算模型参数
  • 解码：根据训练得到的模型参数，从音频推出文本

基于孤立词的GMM-HMM语音识别

问题简化，我们考虑(0-9)数字识别。整体思路：

  • 训练阶段，对于每个词用不同的音频作为训练样本，构建一个生成模型 P ( X ∣ W ) P(X|W) P(X∣W)，W是词，X是音频特征（MFCC、Fbank参考这篇博客）
  • 解码阶段：给定一段音频特征，经过训练得到的模型，看哪个词生成这段音频的概率最大，取最大的那个词作为识别结果。

X t e s t \\mathbf{X}_{test} Xtest​测试特征， P w ( X ) P_w(\\mathbf{X}) Pw​(X)是词 w w w的概率模型， v o c a b vocab vocab是词表：

a n s w e r = arg ⁡ max ⁡ w ∈  vocab  P w ( X test  ) answer =\\underset{w \\in \\text { vocab }}{\\arg \\max } P_{w}\\left(\\boldsymbol{X}_{\\text {test }}\\right) answer=w∈ vocab argmax​Pw​(Xtest ​)

假设我们给每个词建立了一个模型： P o n e ( X ) , P t w o ( X ) . . . P_{one}(X),P_{two}(X)... Pone​(X),Ptwo​(X)...，计算在每个词上的概率，选择所有词中概率最大的词作为识别结果。这样会有几个问题：用什么方法进行建模：DNN，GMM?这些够可以进行建模，但是语音任务的特点是序列性，不定长性，很难使用DNN、GMM直接进行建模。为了解决这些问题，我们可以利用HMM来进行序列建模。

语音是一个序列， P w ( X ) P_w(X) Pw​(X)可以用HMM的概率问题来描述，并且其中的观测是连续概率密度分布，我们可以为每个词建立一个GMM-HMM模型。

建模

语音识别中的GMM，采用对角GMM（协方差为对角阵），因为一般我们使用MFCC特征，MFCC特征各维之间已经做了去相关处理，各维之间相互独立，直接使用对角阵就可以描述，而且对角GMM参数量小。

语音识别中的HMM，采用3状态，左右模型的HMM：

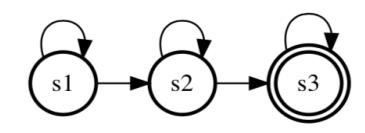
  • 为什么采用3状态？这是前人大量实验给出的经验值；
  • 左右模型的HMM：对于每个状态，它只能跳转到自身或者下一个状态。类似于人的发音过程，连续不可逆。

HMM、GMM语音识别中如何结合？

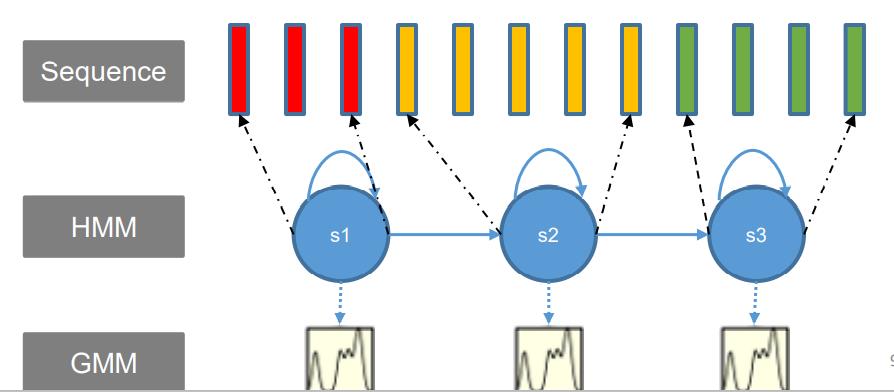
对于每个状态有一个GMM模型，对于每个词有一个HMM模型，当一段语音输入后，根据Viterbi算法得到一个序列在GMM-HMM上的概率，然后通过Viterbi回溯得到每帧属于HMM的哪个状态（对齐）。

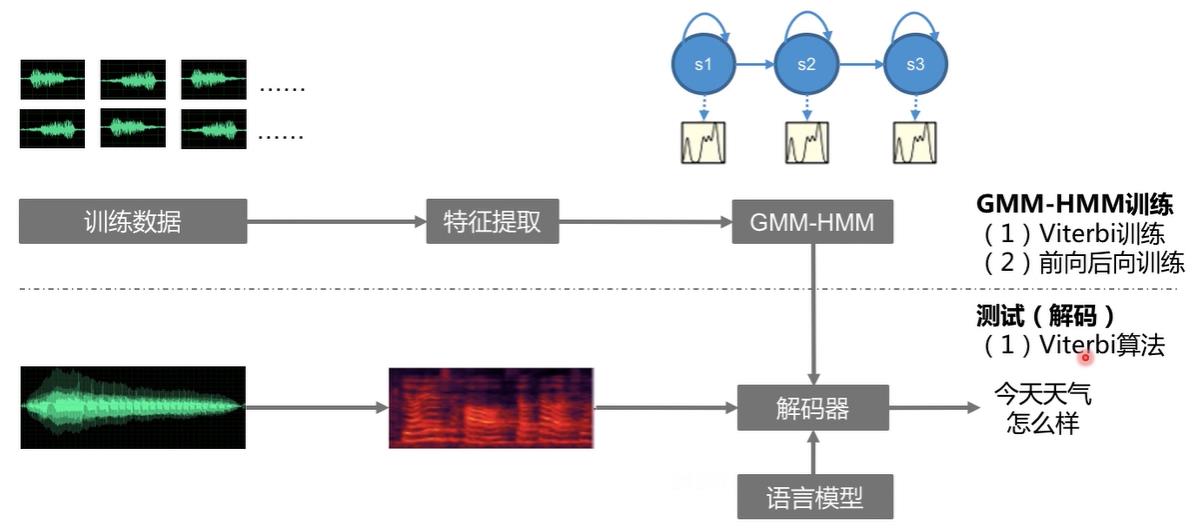
训练

GMM-HMM模型参数：

  • 初始化参数（左右HMM）：这参数没必要
  • 转移参数：自跳或者跳向下一个（两个参数）
  • 观测参数：混合系数、均值、方差

Viterbi训练

  1. E步
    • Viterbi算法得到最优的状态序列（对齐），也就是在t时刻处于状态i上的概率（非0即1）
    • GMM模型中在t时刻处于状态i第k个GMM分量的概率
  2. M步
    • 更新转移参数、GMM参数（混合系数、均值、方差）
  3. 重复E、M步

如何初始化GMM-HMM模型的参数？把语音进行均等切分，给每个状态分配对应的特征，然后去估计初始化的参数。

前向后向训练（Baum-Welch训练）

  1. E步
    • 通过前向后向算法得到在时刻t处于状态i的概率
    • 在时刻t处于状态i且为GMM第k个分量的概率
  2. M步
    • 更新转移参数、GMM参数（混合系数、均值、方差）
  3. 重复E、M步

Viterbi和Baum-Welch学习算法的详细内容参考我之前的文章。

解码

输入：各个词的GMM-HMM模型，未知的测试语音特征。

输出：哪个词。

主要关键点：对所有的词，如果计算 P w ( X t e s t ) P_w(X_{test}) Pw​(Xtest​)。可以通过：前向后算法，或者Viterbi算法（可以回溯到最优的状态序列），一般采用Viterbi算法。

解码主要在图上做，我们现在看one two两个数字识别问题：

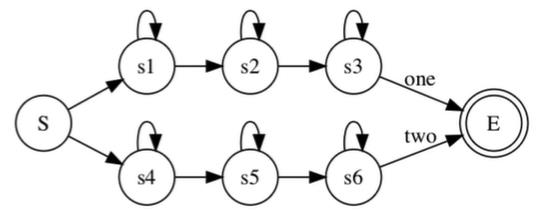
构建HMM模型的拓扑图，下图是紧凑的解码图：

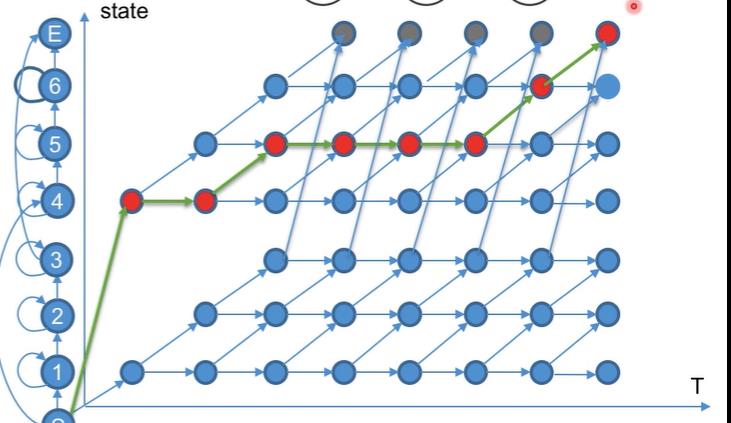
通过Viterbi算法，找过最优的路径得到最终输出的词。那么如果我们需要对连续的多个词识别，需要如何建模？

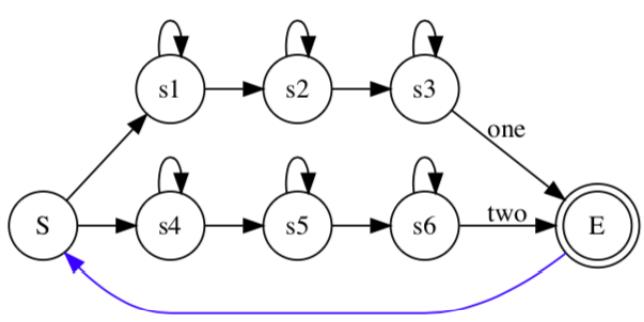
我们只需要再拓扑图上加一个循环连接，对于孤立词，如果达到了识别状态就结束了，对于连续词，如果达到了结束状态，就继续识别下一个词。每个HMM内部还是采用Viterbi算法，在每个时刻对于每个状态选择一条最大概率的路径。因为是并行的，在某个时刻，可能同时会有多个词达到结束状态，分别对应着一段路径，然后又要同时进行下一个词的识别，那么为了避免多余的计算，采用和Viterbi一样的思路，只选取最大概率的路径，扔掉其他。

基于单音素的GMM-HMM语音识别系统

孤立词系统的缺点：

  • 建模单元数、计算量和词典大小成正比
  • OOV（out of Vocabulary）问题，训练中没有这个词，测试中存在这个词；
  • 词的状态数对每个词不用，长词使用的状态数更多

为了克服上边的问题，采用音素建模。每个音素使用3状态结构：

简化问题：假设一句话中包含一个单词，比如one(W AA N)，我们可以很容易得到三个音素的HMM状态图，将状态图进行平滑连接得到one的一整个HMM，然后进行和上述孤立词相同的过程。

问题：如果一句话中包含多个单词？

这个采用和上述相同的方法，加入循环结构，当到达结束状态时进行下一个词的识别。

基于三音素的GMM-HMM语音识别系统

单音素缺点：

  • 建模单元数少，一般英文系统的音素数30-60个，中文的音素数100个左右；
  • 音素的发音受上下文影响，比如：连读、吞音。

可以考虑音素的上下文，一般考虑前一个/后一个，称为三音素，表示为A-B+C。比如：KEEP K IY P => #-K+IY, K-IY+P, IY-P+#。

问题1：假设有N个音素，一共有多少个三音素？ N 3 N^3 N3

问题2：有的三音素训练数据少或者不存在，怎么办？

问题3：有的三音素在训练中不存在，但在测试中有怎么办?

问题2和问题3通过参数共享解决，下文将介绍决策树。

参数共享

共享可以在不同层面：

  • 共享高斯模型：所有状态都用同样的高斯模型，只是混合权重不一样；
  • 共享状态：允许不同的HMM模型使用一些相同的状态；
  • 共享模型：相似的三音素使用同样的HMM模型。

笔者主要介绍共享状态，可以采用自顶向下的拆分，建立决策树来聚类。

三音素决策树

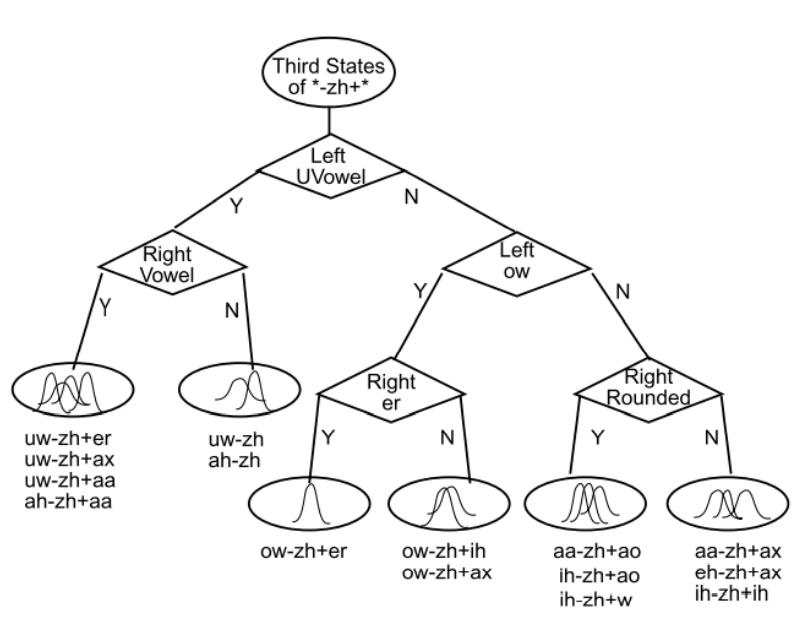
决策树是一个二叉树，每个非叶子节点上会有一个问题，叶子节点是一个绑定三音素的集合。绑定的粒度为状态（A-B+C和A-B+D的第1个状态绑定在一起，并不表示其第二第三个状态也要绑定在一起），也就是B的每个状态都有一颗小的决策树。

问题集

常见的有：

  • 元音 AA AE AH AO AW AX AXR AY EH ER …
  • 爆破音 B D G P T K
  • 鼻音 M N NG
  • 摩擦音 CH DH F JH S SH TH V Z ZH
  • 流音 L R W Y

问题集的构建：语言学家定义，Kaldi中通过自顶向下的聚类自动构建问题集。

决策树构建

初始条件类似图中的根节点，"*-zh+*"，从问题集中选择合适的问题，分裂该节点，使相近的三音素分类到相同的节点上。假设根节点所有三音素对应的特征服从一个多元单高斯分布，可以计算出该单高斯分布的均值和方差，则可以计算出该节点任意一个特征在高斯上的似然。

模型：假设其服从单高斯分布，并且各维独立，也就是对角GMM
Pr ⁡ [ x ] = 1 ∏ k = 1 N ( 2 π σ k 2 ) 1 / 2 ∏ k = 1 N exp ⁡ ( − 1 2 ( x k − μ k ) 2 σ k 2 ) \\operatorname{Pr}[x]=\\frac{1}{\\prod_{k=1}^{N}\\left(2 \\pi \\sigma_{k}^{2}\\right)^{1 / 2}} \\prod_{k=1}^{N} \\exp \\left(-\\frac{1}{2} \\frac{\\left(x_{k}-\\mu_{k}\\right)^{2}}{\\sigma_{k}^{2}}\\right) Pr[x]=∏k=1N​(2πσk2​)1/21​k=1∏N​exp(−21​σk2​(xk​−μk​)2​)
似然
L ( S ) = − 1 2 ∑ i = 1 m [ ∑ k = 1 N log ⁡ ( 2 π σ k 2 ) + ∑ k = 1 N ( x i k − μ k ) 2 σ k 2 ] = − 1 2 [ m ∑ k = 1 N log ⁡ ( 2 π σ k 2 ) + m ∑ k = 1 N σ k 2 σ k 2 ] = − 1 2 [ m N ( 1 + log ⁡ ( 2 π ) ) + m ∑ k = 1 N log ⁡ ( σ k 2 ) ] \\begin{aligned} L(S) &=-\\frac{1}{2} \\sum_{i=1}^{m}\\left[\\sum_{k=1}^{N} \\log \\left(2 \\pi \\sigma_{k}^{2}\\right)+\\sum_{k=1}^{N} \\frac{\\left(x_{i k}-\\mu_{k}\\right)^{2}}{\\sigma_{k}^{2}}\\right] \\\\ &=-\\frac{1}{2}\\left[m \\sum_{k=1}^{N} \\log \\left(2 \\pi \\sigma_{k}^{2}\\right)+m \\sum_{k=1}^{N} \\frac{\\sigma_{k}^{2}}{\\sigma_{k}^{2}}\\right] \\\\ &=-\\frac{1}{2}\\left[m N(1+\\log (2 \\pi))+m \\sum_{k=1}^{N} \\log \\left(\\sigma_{k}^{2}\\right)\\right] \\end{aligned} L(S)​=−21​i=1∑m​[k=1∑N​log(2πσk2​)+k=1∑N​σk2​(xik​−μk​)2​]=−21​[mk=1∑N​log(2πσk2​)+mk=以上是关于基于GMM-HMM的语音识别系统的主要内容，如果未能解决你的问题，请参考以下文章

我们基于kaldi开发的嵌入式语音识别系统升级成深度学习啦

GMM-HMM声学模型

基于DNN-HMM的语音识别技术

[转] 语音识别基本原理介绍----gmm-hmm中的embedded training （嵌入式训练）

如何解释语音识别的技术原理？

声学模型GMM-HMM