嵌入式DSP开发的定点数和浮点数

Posted 2021-06-09 一只学习的猫

文章目录

• 1 前言
• 2 什么是原码、反码和补码
• • 2.1 原码表示法
  • 2.2 反码表示法
  • 2.3 补码表示法
  • 2.4 小结
  • 2.4 在计算机中为什么采用补码来进行存储
• 3 十进制的数和二进制数之间的转换
• • 3.1 十进制的数转换为二进制数
  • 3.2 二进制的数转换为十进制数
• 4 定点数和浮点数的概念
• • 4.1 定点数
  • • 4.1.1 定点数存储格式（Q格式）
    • 4.1.2 定点数与浮点数之间的转换
    • • 4.1.2.1 浮点数到定点数
      • 4.1.2.2 定点数到浮点数
      • 4.1.2.2 定点数到定点数
    • 4.1.3 定点数能够表示的数值范围与精度
    • 4.1.3 定点数的动态范围
    • 4.1.3 定点数的算术运算
    • • 4.1.3.1 定点数加减运算
      • 4.1.3.2 定点数乘法运算
    • 4.1.1 定点DSP芯片
  • 4.2 浮点数
  • • 4.2.1 科学计数法
    • 4.2.1 浮点数的存储格式
    • 4.2.2 浮点数能够表示的数值范围与精度
    • 4.2.2 浮点运算
• 5 总结

1 前言

在DSP芯片的介绍中，我们常常会听到定点数运算、浮点数运算，那到底什么是定点数，什么是浮点数呢？为回答这个问题，本篇文章打算谈一谈定点数和浮点数的一些基本概念，在此之前作为预备知识，会先介绍一些关于原码、反码和补码的内容，然后介绍一下十进制数与二进制数之间的转化，最后再介绍定点数和浮点数。

2 什么是原码、反码和补码

2.1 原码表示法

最高位为符号位(正数为0，负数为1)，其它位为符号位。
一个正数的原码，是按照十进制绝对值大小转换成的二进制数；
一个负数的原码，是按照十进制绝对值大小转换成的二进制数，然后最高位补1。
例子：
假设一个int类型的数，数值是5，则在计算机中的表示为：
00000000 00000000 00000000 00000101
5转换成二制是101，不过int类型的数占用4字节（32位），所以前面填了一堆0。
-5的表示为符号位为1，其它位表示数值，则在计算机中的表示为：
10000000 00000000 00000000 00000101。

2.2 反码表示法

如果是正数，则按照原码形式不变；
如果是负数，则符号位不变，该数的原码的其它位按位取反。
如上例，+5的反码和原码相同，都为00000000 00000000 00000000 00000101，
-5的反码为符号位不变，其它位按位取反，11111111 11111111 11111111 11111010

2.3 补码表示法

如果是正数，则按原码形式不变；
如果是负数，则符号位不变，该数的原码其它位按位取反再加1。
如上例，+5的补码和原码相同，都为00000000 00000000 00000000 00000101，
-5的补码为原码的符号位不变，其它位按位取反然后加1，即为：
11111111 11111111 11111111 11111011

2.4 小结

在n位的机器数中，最高位为符号位，该位为零表示为正，为1表示为负； 其余n-1位为数值位，各位的值可为0或1。
当真值为正时:原码、反码、补码数值位完全相同；
当真值为负时: 原码的数值位保持原样，反码的数值位是原码数值位的各位取反，补码则是反码的最低位加1， 注意进位不能进到符号位。
结论：
（1） 正数
原码反码补码
（2）负数
原码数值位保持不变，符号位为1
反码符号位为1 不变，原码其它位取反
补码==符号位为1 不变，反码加1

2.4 在计算机中为什么采用补码来进行存储

在计算机中，数据是以补码的形式存储的。
为什么要采用补码存储呢？这是为了简化计算机基本运算电路，使加减法都只需要通过加法电路实现，也就是让减去一个正数或加上一个负数这样的运算可以用加上一个正数来代替。于是改变负数存储的形式，存储成一种可以直接当成正数来相加的形式，这种形式就是补码（补码可以直接进行加减运算）。
具体参见网址：https://blog.csdn.net/a1285398438/article/details/88396285。
https://blog.csdn.net/niusi1288/article/details/96452179

3 十进制的数和二进制数之间的转换

3.1 十进制的数转换为二进制数

（1）对于正整数：
“除2取余，逆序排列”；
（2）对于小数：
“乘2取整，顺序排列”；
举例子：
0.6252=1.25取出整数部分1
0.25*2=0.5取出整数部分0
0.52=1========取出整数部分1
所以：
（0.625）10=（0.101）2
（3）对于正整数+小数：
整数部分的二进制表示和小数部分的二进制表示相加即可；
比如上述的173.625=173+0.625，最后得到的二进制表示为：
（173.625）10=（10101101.101）2
（4）对于负整数：
先将对应的负整数的原码表示出来，然后取反再加1（符号位不取反）；
（5）对于负整数+小数：
可以将负实数写成负整数+小数的形式，然后分别表示出负整数的二进制补码表示和小数部分的二进制表示，然后相加即可。

3.2 二进制的数转换为十进制数

方法：按权展开求和。
注意，对于负的十进制数，需要先将二进制减一再取反，得到十进制表示，再进行转换。

具体的转换原理参见：
https://baike.baidu.com/item/%E5%8D%81%E8%BF%9B%E5%88%B6%E8%BD%AC%E4%BA%8C%E8%BF%9B%E5%88%B6/393189?fr=aladdin

4 定点数和浮点数的概念

在用二进制存储数据时，如果小数点的位置事先已有约定，不再改变，此类数称为“定点数”。相比之下，如果小数点的位置可变，则称为“浮点数”。

4.1 定点数

定点数的本质是小数，整数只是其表现形式，确定小数点的位置称为定标。常用的定点数有两种表示形式：
（1） 如果小数点位置约定在最低数值位的后面，则该数只能是定点整数；
（2） 如果小数点位置约定在最高数值位的前面，则该数只能是定点小数。
目前计算机中多采用定点纯整数表示，因此将定点数的运算简称为整数运算。
定点数表达法的缺点在于其形式过于僵硬，固定的小数点位置决定了固定位数的整数部分和小数部分，不利于同时表达特别大的数或者特别小的数。最终，绝大多数现代的计算机系统采纳了所谓的浮点数表达方式。
对于各种整型数据所能表达的数值范围如下：

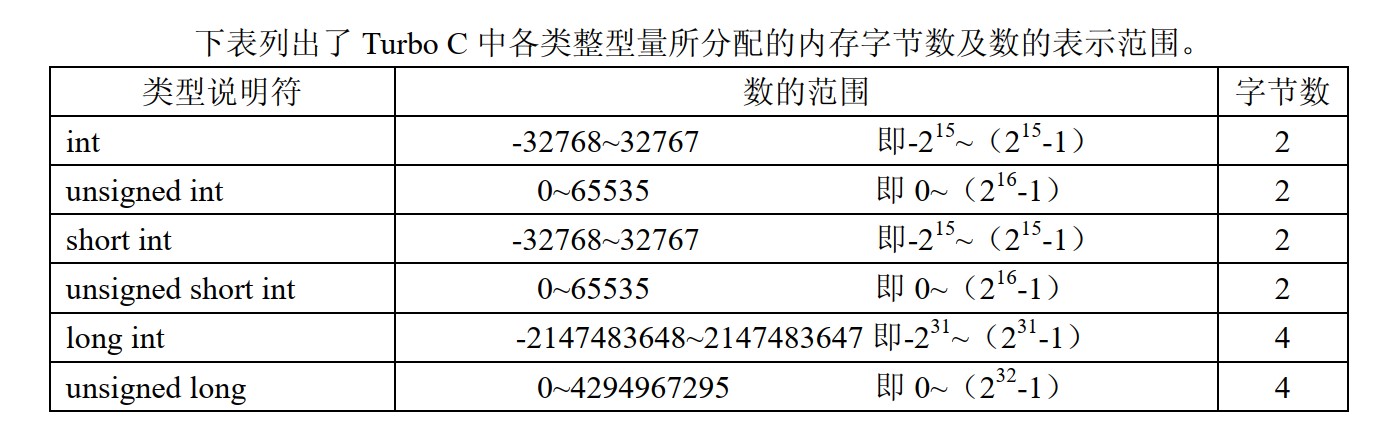
4.1.1 定点数存储格式（Q格式）

整数小数点固定在最后，定点数小数位固定使用Qn格式（n表示小数位数）表示，两者都使用二进制补码形式表示。
假设是8位字长，则存储格式是：1位符号位+(7-n)位整数位+n位小数位

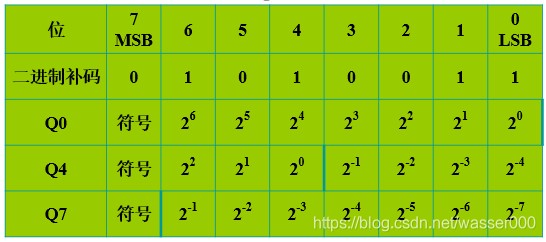
比如Q4格式存储的定点数：01010011b
对应的定点数为：12^2+1*20+12^(-3) +1*2^(-4)=5.1875

4.1.2 定点数与浮点数之间的转换

定点数与浮点数转化时需要使用2^n的关系进行转化。

4.1.2.1 浮点数到定点数

4.1.2.2 定点数到浮点数

4.1.2.2 定点数到定点数

4.1.3 定点数能够表示的数值范围与精度

假设是N位字长的定点运算，假设有n位小数，则：
数值范围：

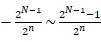
精度:

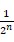
由于符号位占1位，所以数据位为N-1，n越大，能表示的数值范围越小，但精度越高。例如，当N=16时，n取不同值时，可表示的数值范围和精度如下所示：

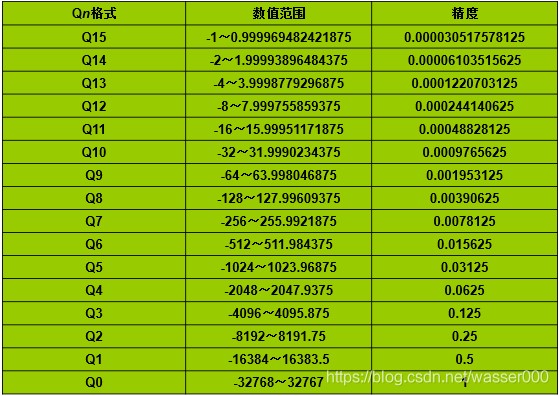
4.1.3 定点数的动态范围

动态范围是指数据格式中最大值与最小值之比。
N位定点数动态范围：

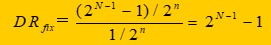
分贝表示：dsp大多采用16位定点数，动态范围为90.3db。

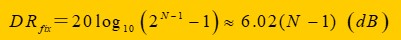
DSP大多采用16位定点数，运算硬件实现较为简单，更大动态范围应用可以使用拓展字长方式。

4.1.3 定点数的算术运算

定点运算的硬件实现较为简单，功耗较小，主要注意的是数据的定标、溢出以及误差。

4.1.3.1 定点数加减运算

首先需要保证小数点对齐，但是运算结果可能会溢出。如果进位位与最高位（MSB）相同无溢出，不同则有溢出。处理溢出通常有饱和模式与非饱和模式，饱和模式溢出时会对溢出进行限幅，非饱和模式不会处理，例如：

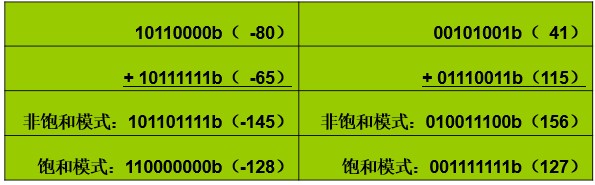
注意表中都是二进制补码。

4.1.3.2 定点数乘法运算

DSP处理器都有硬件乘法器和乘法指令，可实现单周期乘法运算。二进制乘法运算包含了移位与加法运算。
定点数乘法不要求小数点位统一，两个相乘数分别为Qn和Qm格式，字长为N，结果为Q(n+m)格式，字长为2N。
在进行运算时，需要字长保持不变，则两个定点小数作乘法运算，结果左移一位，保存高位得到运算结果，结果为Qm（m≤ n）格式。
若整数乘小数，则输出结果为整数，丢弃后8位为截尾误差。误差小于等于Qn格式精度的一半，即小于等于 1/(2^(n+1)) 。单次计算误差不大，但连续计算，尤其是递归算法中，误差影响较大。
整数相乘，结果为Q0格式，需查询标志位确定保存的位数，结果不需要左移一位。若结果没有超出8位数的表示范围时，结果在低8位，保存低8位。若结果超出8位数的表示范围时，则高8位也包含乘积结果，应保存整个16位结果。

4.1.1 定点DSP芯片

在定点DSP芯片中，采用定点数进行数值运算，其操作数一般采用整型数来表示。一个整型数的最大表示范围取决于DSP芯片所给定的字长，一般为16位或24位。显然，字长越长，所能表示的数的范围越大，精度也越高。
以16位字长为例。DSP芯片的数以2的补码形式表示。每个16位数用一个符号位来表示数的正负，0表示数值为正，1则表示数值为负。其余15位表示数值的大小。对DSP芯片而言，参与数值运算的数就是16位的整型数。但在许多情况下，数学运算过程中的数不一定都是整数。那么，DSP芯片是如何处理小数的呢？应该说，DSP芯片本身无能为力（需要人为将小数转化为整数进行运算）。那么是不是说DSP芯片就不能处理各种小数呢？当然不是。这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。这就是数的定标。不同的定标对应取不同n的Q格式。

4.2 浮点数

4.2.1 科学计数法

比如123.45用十进制科学计数法表示为：1.234510^2
其中给出几个概念：1.2345称为尾数(有效数字的非正式说法)，10为基数，2为指数（exponent，也称为阶码）。浮点数利用指数达到了浮动小数点的效果，从而可以灵活地表达更大范围的实数。对于一个二进制的数，比如1011.01，用科学计数法可以表示为：1.011012^3。
小数部分占的位（ bit）数愈多，数的有效数字愈多（有效数字指的是从左往右第一个不为0的数开始的数的位数），精度愈高。指数部分占的位数愈多，则能表示的数值范围愈大。换句话说就是，浮点数所能表示的范围取决于阶码；精度取决于尾数。

4.2.1 浮点数的存储格式

计算机中是用有限的连续字节保存浮点数的。保存这些浮点数当然必须有特定的格式，C中的浮点数类型float和double采用了IEEE 754标准中定义的单精度32位浮点数类型和64位双精度浮点数的格式。
IEEE 754标准，是一种科学计数法。在 IEEE 标准中，浮点数是将特定长度的连续字节的所有二进制位分割为特定宽度的符号域，指数域和尾数域三个域，其中保存的值分别用于表示给定二进制浮点数中的符号，指数和尾数。这样，通过尾数和可以调节的指数（所以称为"浮点"）就可以表达给定的数值了。浮点数格式：

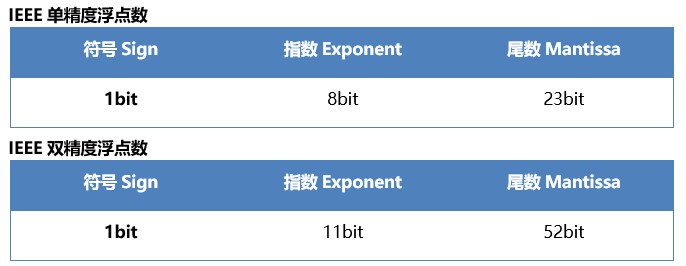
1. 第一个域为符号域。其中 0 表示数值为正数，而 1 则表示负数。
2. 第二个域为指数域。其中单精度数为 8 位，双精度数为 11 位。以单精度数为例，8 位的指数为可以表达 0 到 255 之间的 255 个指数值。但是，指数可以为正数，也可以为负数。为了处理负指数的情况，实际的指数值按要求需要加上一个偏差（Bias）值作为保存在指数域中的值，单精度数的偏差值为 127，而双精度数的偏差值为 1023。比如，单精度的实际指数值 0 在指数域中将保存为 127；而保存在指数域中的 64 则表示实际的指数值 -63。 偏差的引入使得对于单精度数，实际可以表达的指数值的范围就变成 -127 到 128 之间（包含两端）。我们后面还将看到，实际的指数值 -127（保存为 全 0）以及 +128（保存为全 1）保留用作特殊值的处理。这样，实际可以表达的有效指数范围就在 -127 和 127 之间。
3. 第三个域为尾数域，其中单精度数为 23 位长，双精度数为 52 位长。除了我们将要讲到的某些特殊值外，IEEE 标准要求浮点数必须是规范的。这意味着尾数的小数点左侧必须为 1，因此我们在保存尾数的时候，可以省略小数点前面这个 1，从而腾出一个二进制位来保存更多的尾数。这样我们实际上用 23 位长的尾数域表达了 24 位的尾数。比如：对于单精度数而言，二进制的 1001.101（对应于十进制的 9.625）可以表达为 1.001101 × 23，所以实际保存在尾数域中的值为 0011 0100 0000 000 0000 0000，即去掉小数点左侧的 1，并用 0 在右侧补齐。
   举例：
   浮点数：+27.5
   二进制：11011.1
   指数式（754标准）：1.10111*2^4，即尾数是1.10111，指数为4，符号位为0
   因此符号域为0
   指数域的值为4+127=131 对应二进制为：1000 0011
   尾数域为10111 000000000000000000
   因此在计算机中的单精度存储：
   
   0100 0001 1101 1100 0000 0000 0000 0000 ，在DSP中的十六进制表示为0x41DC0000
   将十六进制表示的浮点数转换成十进制，则首先要读出浮点数的数符s，阶码e，十进制尾数x,然后按照如下计算公式计算对应的十进制数：(-1)^s * (1 + x) * 2^(e - 127)

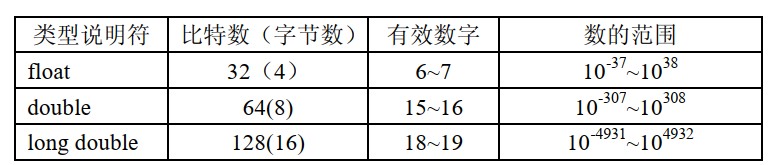
4.2.2 浮点数能够表示的数值范围与精度

4.2.2 浮点运算

浮点器件结构较为复杂，但是精度较高，高级语言容易支持。
参考网址：https://blog.csdn.net/tercel_zhang/article/details/52537726

5 总结

主要介绍了定点数和浮点数的一些基本概念。之后在嵌入式开发中再给出一些相关的实例哈~~~~