多阶二叉树模型

Posted 2021-06-09 期权世界

上海濡圣投资管理有限公司

为了让一阶二叉树模型更符合实际，我们把一阶段分成多个阶段，即二阶、三阶，甚至 100 阶等，然后查看 Delta 对冲在多阶模型中是否同样有效。

先来看二阶二叉树模型。二阶二叉树模型由开始、中间、到期三个时点组成。这里假定利率为 10%。在各个时点上，矩形的上半部分为标的资产的价格，下半部 分为认购期权的价格，如图所示。

与前面的案例不同，到期时标的资产的价格不再是两种情形而是三种情形。二叉树模型的阶段越多到期时标的资产价格可能的情形也会越多。本模型的阶段每增加一个，标的资产价格变化的幅度就会发生改变。假设上涨和下跌的幅度一律为 1000。多阶二叉树模型应该如何上手？我们可以采用数学归纳法求解多阶二叉树模型。所不同的是，我们不知道初值，反而知道终值（期权到期价格）。另外，利用一阶模型中所用的方法也可知道各阶段和其前一阶段的关系。因此，依靠数学归纳法可以求出认购期权价格。

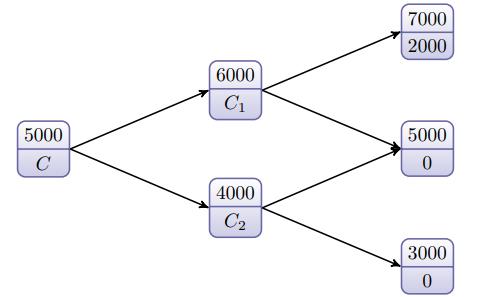
图：二阶二叉树模型

在图中，该认购期权的行权价为 5000 元，因此到期时期权价值在标的资产价格为 7000 元、5000 元、3000 元时分别为 2000 元、0、0。在这里关注到期价格变为 7000 元和 5000 元的情形，及其前一时点（6000，C1）。仔细观察该情形可以发现， 该问题和求解初始价格为 6000 元、行权价为 5000 元的认购期权一阶二叉树模型的求解方法相同，即与一阶二叉树模型中求期权合理价格时的结构相同，只是数字稍有变化。重复之前在一阶二叉树模型的方法可以求出 C1，同样的方法也可以求出 C2，再利用 C1、C2，最终求出开始阶段认购期权的合理价格 C。

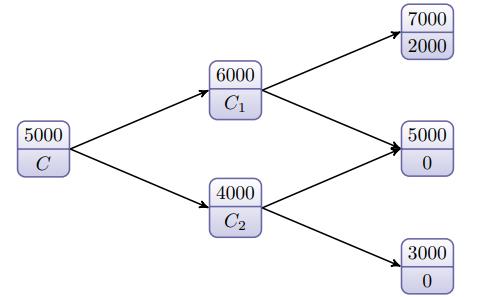
图：二阶二叉树模型

总之，只要我们知道最终阶段（到期）的期权价格，就可以求出其前一时点的认购期权合理价格，再利用该时点的认购期权合理价格，求出再前一阶段的期权合理价格，重复该方法最终可以求出开始阶段认购期权的合理价格。

    

利用这个案例，我们一起来求开始阶段的认购期权合理价格。在一阶二叉树模 型中，已知下一阶段期权价格（CU,CD）和标的资产价格（SU,SD）的情况下，求解期初期权合理价格的公式如下：

    

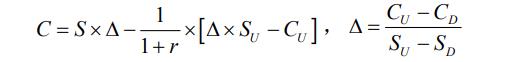
利用公式求 C1、C2、C。在给定的条件中，SU=7000，SD=5000，CU=2000， CD=0，r=0.1，带入公式得 C1 = 1454.55。虽然 C2 也可以用如上公式求得，但从下图可以看到，C2 在到期时不管标的资产上涨或下跌，期权价值均为 0。

图：二阶二叉树模型中求认购期权合理价格

到期时价值恒为 0 的期权现在的价值也只能为 0。结果，二阶二叉树模型还原为如下图所示的一阶二叉树模型。

图：还原为一阶二叉树模型

    

二阶模型还原为一阶模型，同样三阶模型也可还原为二阶模型，二阶模型又还原为一阶模型。因此，即便是 100 阶二叉树模型，虽然计算量会较大，但依然能求出二叉树模型开始时点的期权合理价格。