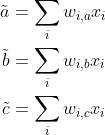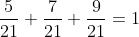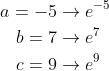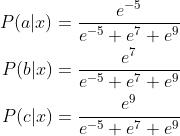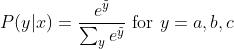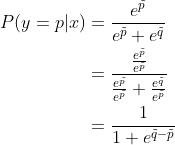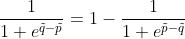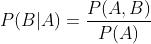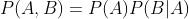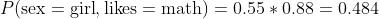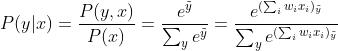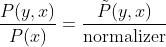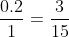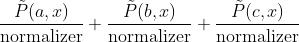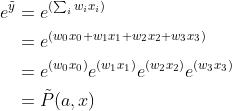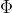sigmoid和softmax函数详解

Posted 2023-03-31

参考技术A 参考: https://baijiahao.baidu.com/s?id=1636737136973859154&wfr=spider&for=pc

在一个最近的一个项目中,发现自己对sigmoid函数和softmax函数的概念和用法比较模糊,特地做一下总结

假设一张图片丢进一个神经网络(例如resnet50),最后的输出为一个向量,如[-0.5, 1.2, -0.1, 2.4],分别对应四中不同的标签.

Sigmoid函数或Softmax函数可以将分类器的原始输出值映射为概率。那么什么时候用到sigmoid,什么时候用softmax呢?

下图显示了将前馈神经网络的原始输出值（蓝色）通过Sigmoid函数映射为概率（红色）的过程：

然后采用Softmax函数重复上述过程：

如图所示，Sigmoid函数和Softmax函数得出不同结果。

原因在于，Sigmoid函数会分别处理各个原始输出值，因此其结果相互独立，概率总和不一定为1，如图0.37 + 0.77 + 0.48 + 0.91 = 2.53。

相反，Softmax函数的输出值相互关联，其概率的总和始终为1，如图0.04 + 0.21 + 0.05 + 0.70 = 1.00。因此，在Softmax函数中，为增大某一类别的概率，其他类别的概率必须相应减少

Sigmoid函数如下所示（注意e）：

在该公式中，σ表示Sigmoid函数，σ（zj）表示将Sigmoid函数应用于数字Zj。 “Zj”表示单个原始输出值，如-0.5。 j表示当前运算的输出值。如果有四个原始输出值，则j = 1,2,3或4。在前面的例子中，原始输出值为[-0.5,1.2，-0.1,2.4]，则Z1 = -0.5，Z2 = 1.2，Z3 = -0.1，Z4 = 2.4。

所以，

Z2，Z3、Z4 的计算过程同上。

由于Sigmoid函数分别应用于每个原始输出值，因此可能出现的输出情况包括：所有类别概率都很低一种类别的概率很高但是其他类别的概率很低，多个或所有类别的概率都很高。

下图为Sigmoid函数曲线：

Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）

构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出值 。

Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。

Softmax函数表述如下：

除分母外，为综合所有因素，将原始输出值中的e ^ thing相加，Softmax函数与Sigmoid函数差别不大。换言之，用Softmax函数计算单个原始输出值（例如Z1）时，不能只计算Z1，分母中的Z1，Z2，Z3和Z4也应加以计算，如下所示：

区分手写数字时，用Softmax函数处理原始输出值，如要增加某一示例被分为“8”的概率，就要降低该示例被分到其他数字（0,1,2,3,4,5,6,7和/或9）的概率。

Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）

构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。

Softmax与Sigmoid函数的联系

译自：http://willwolf.io/2017/04/19/deriving-the-softmax-from-first-principles/

本文的原始目标是探索softmax函数与sigmoid函数的关系。事实上，两者的关系看起来已经是遥不可及：一个是分子中有指数！一个有求和！一个分母中有1！。当然，最重要的是两个的名称不一样。

推导一下，很快就可以意识到，两者的关系可以回溯到更为泛化的条件慨率原理的建模框架（back out into a more general modeling framework motivated by the conditional probability axiom）。本文首先探索了sigmoid函数是一种特殊的softmax函数，以及各自在Gibbs distribution, factor products和概率图模型方面的理论支撑。接下来，我们继续展示概框架如何自然的扩展到canonical model class，如softmax回归，条件随机场（Conditional Random Fields）,朴素贝叶斯（Naive Bayes）以及隐马尔科夫模型(Hidden Markov Model)。

目标（Our Goal）

下图是一个预测模型（predictive model），其中菱形表示接收输入，并产生输出。输入向量，有3种可能的输出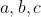：。模型的目标在于在输入的条件下产生各种输出的概率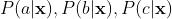：。概率是位于闭区间[0,1]的一个实数值。

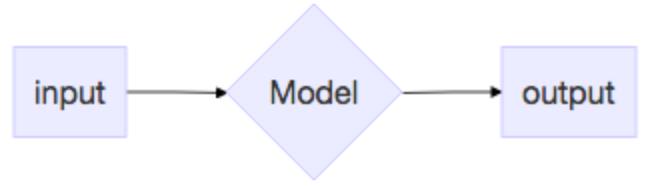
输入对输出的影响（How does the input affect the output?）

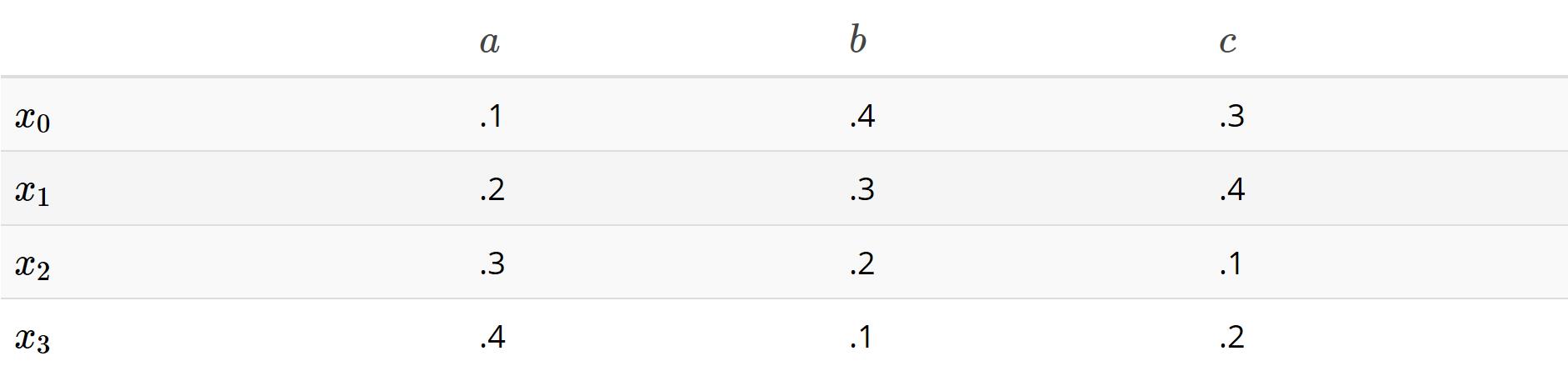
每个输入是4个数的列表（输入向量是4维），每一维度对各个可能的输出影响程度不同，这里我们称它为权重（weight）。4个输入数据乘以3个输出，代表了12个不同的权重。可能如下表所示：

生成输出（Producing an Output）

给定一个输入向量，我们的模型将使用上述权重来生成输出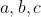。这里假设每个输入元素的影响是加性的（The effect of each input element will be additive.）。至于原因留待后续解释。

这些求和公式会对模型的输出结果产生贡献。最大的数将会胜出。例如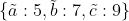，若上式得到的结果是，则我们的模型会得到结论：最大可能产生c。

转换为概率（Converting to Probabilities）

之前说过，我们的目标在于获得概率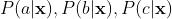：。其中为黑体，为了表示任意的输入向量。当给定一个具体的输入向量时，我们用花体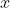表示，这样我们的目标可以更精确的表示为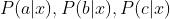：。至此，我们已经获得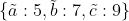。为了将这些值转换成一个概率，也就是闭区间[0,1]之间的一个实数值，我们只需要用这些值的和去除原始值。 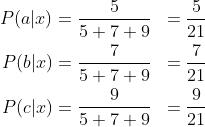最后我们得到一个合理的概率分布，所有值的和相加为1.

如果我们得到的值是负数怎么办？（What if our values are negative?）

如果其中的一个未经正则化的概率的值为负数，例如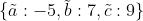，，那么所有的都会被破坏。该值对应的概率值也不会是一个合理的概率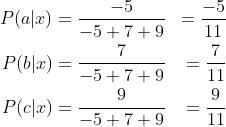， 因为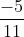它不能落在[0,1]闭区间之内。

为了保证所有没有正则化的概率值为正数，我们必须用一个函数对这些值进行处理，以保证能够产生一个严格的正实数。简单来说，就是指数函数，我们选额欧拉数e作为底。这种选择的原理有待后续解释。

这样我们正则化后的概率，也就是合法的概率，如下式所示：

泛化表示为：，也就是softmax函数。

与Sigmoid函数的联系（Relationship to the sigmoid）

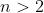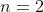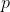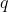如果说Softmax可以得到在多于两个（）不同的输出上的一个合理的概率分布，那么sigmoid可以得到针对两种输出（）的一个合理的概率分布。也就是说，sigmoid仅仅是softmax的一个特例。用定义来表示，假设模型只能产生两种不同的输出：和，给定输入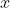，我们可以写出sigmoid函数如下：

然而，值得注意的是，我们只需要计算一种结果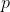的产生概率，因为另外一种结果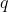的产生概率可以由概率分布的性质得到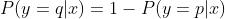：。接下来，我们对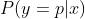的产生概率的表示进行扩展：

然后，对该分式的分子和分母都同时除以，得到：

最后，我们可以用该式代入求另一种结果的产生概率的式子中得到：

该等式是欠定的（underdetermined），由于等式中有多于1个的未知变量。如此说来，我们的系统可以有无穷多组解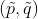。因此，我们对上式进行简单的修改，直接固定其中一个值。例如：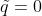

这就是sigmoid函数，最终，我们得到：

为什么这些未正则化概率值是求和得到（影响是加性的）？（Why is the unnormalized probability a summation?）

我们理所当然的认为canonical线性组合的语义是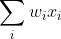。但是为什么先求和？

为了回答这个问题， 我们先复述一下我们的目标：给定输入，预测各种可能结果的产生概率，即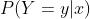。接下来，我们重新看一下条件概率的定义式：

发现这个式子很难解释，我们对这个式子重新变化一下，以或则某些直觉：

得到的信息是：同时观测到A与B的值的概率，也就是A与B的联合概率，等于观测到A的概率乘以给定A观测到B的概率。

例如，假设生一个女孩的概率是0.55，而女孩喜欢数学的概率是0.88，因此，我们得到：

现在，我们对原始的模型输出，利用条件概率的定义式，进行重写：

值得注意的是，这里采用指数函数，以保证将每个未正则的概率值转换为一个严格概率值。技术上来讲，这个数字称为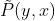，因为可能大于1，所以并非一个严格的概率，我们需要引入另一个项到我们的等式链中：

例如，我们的算术等式：

等式左边的项：

分子是一个严格的联合概率分布。

分母为观测到任意一个x值的概率，为1

等式右边的项：

分子是一个严格的正的未经归一化的概率值

分母是某个常数，以保证和为1。这里归一化项称为partition function。

知道了这些，我们可以对softmax等式中的分子进一步分解：

Lemma:若我们的输出函数softmax函数通过指数函数得到一个多个可能结果上的合理的条件概率分布，那么下述结论肯定成立：该softmax函数的输入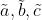（）必须是原始输入元素的加权求和模型。

上述Lemma成立的前提是我们首先接收这样的事实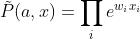：。从而引出来Gibbs distribution。

（二）Gibbs Distribution

Gibbs Distribution给出了一个结果集合上的未归一化的联合概率分布，类似于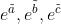，定义如下：

其中定义了一个factor的集合。

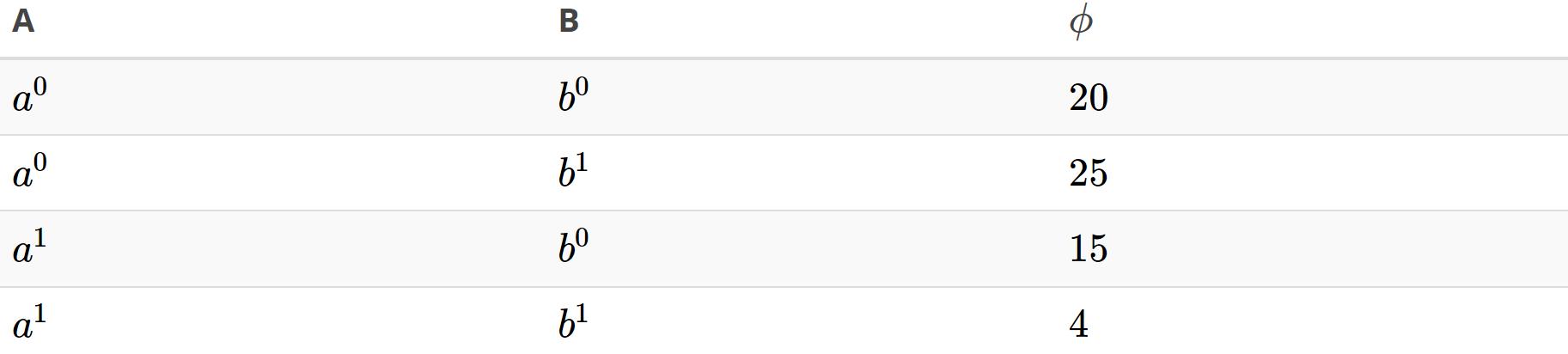
Factor本质为满足下面两个条件的函数：（1）将随机变量作为输入，所有输入随机变量构成的列表称为scope；（2）针对每个可能的随机变量的组合值（即scope的叉积空间中的点），返回一个值。例如，scope为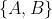的factor可能如下所示：

 

（三）Softmax regression

未完待续