排序4-堆排序与海量TopK问题

Posted 2021-06-08 无聊的马岭头

目录

• 一、堆排序
• • • • .堆排序算法
• 二、海量TopK问题

一、堆排序

（1）堆是一颗完全二叉树
（2）堆的每个节点的值都大于或等于其左右孩子节点称为大堆
（3）堆的每个节点的值都小于或等于其左右孩子节点称为小堆
堆：具备着上面条件的就称之为堆

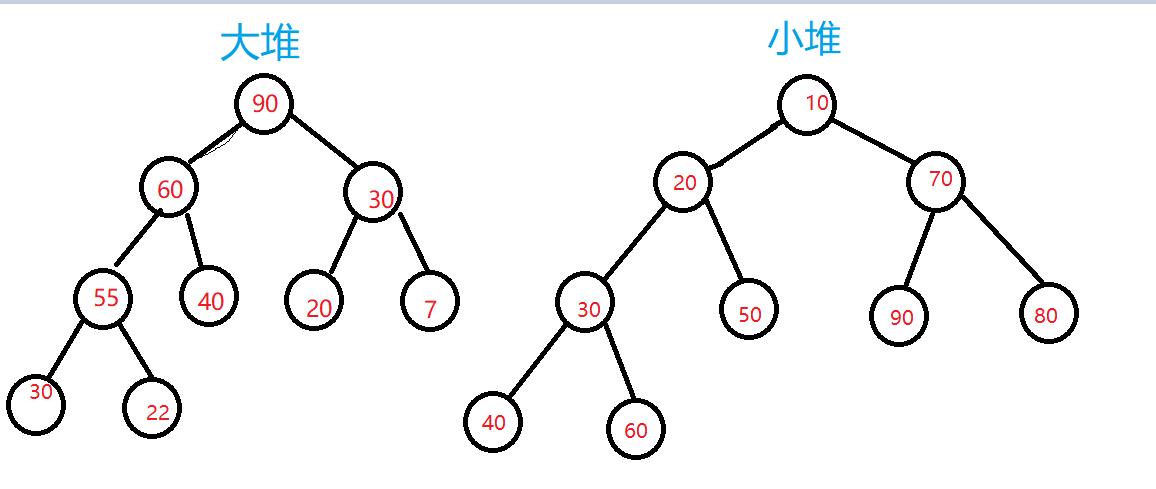
我们可以看出大堆的堆顶是最大值，小堆的堆顶是最小值。
从堆中需要注意：跟节点一定是最大（小）者。

堆的结构：
拿上面大堆做例子：如果将大堆层序遍历存入数组，则满足以下关系

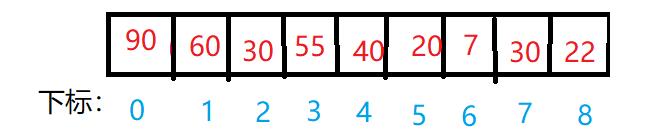
左孩子坐标=2父亲坐标+1
右孩子标=2父亲坐标+2

我们讲这个堆结构，其目的就是为了堆排序用的。

.堆排序算法

堆排序：将待排序的序列构造成一个大（小）堆，整个序列的对大（小）值就是堆顶的根节点。将它拿走，然后把剩余的n-1个序列重新构造成一个堆，就可以得到次大（小）的值，如此反复，便能得到一个有序序列了。

堆的向下调整法：
前提：左右子树必须是堆
通过向下调整，使整颗树都成堆

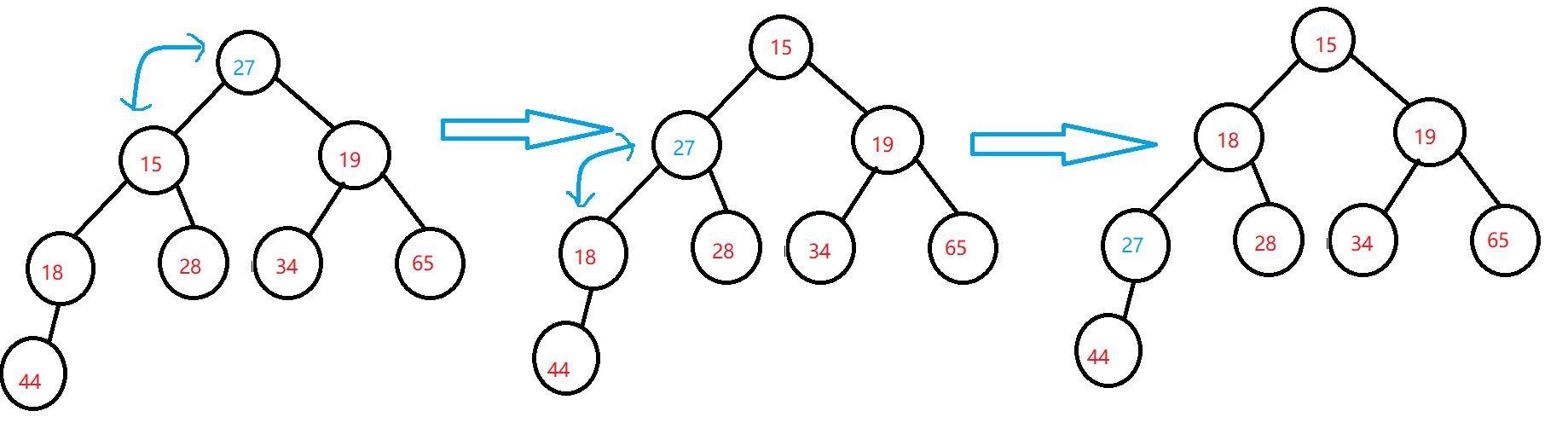
1. 选出左右孩子中小的那一个。
2. 小的孩子跟父亲比。
3. 如果小的孩子比父亲小，则跟父亲交换，并且把原本的原来孩子的位置继续往下调。
4. 如果小的孩子比父亲大，则不需处理，调整完成。

void Swap(int *p,int *q)
{
	int temp = *p;
	*p = *q;
	*q = temp;
}


void AdJustDown(int *arr,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1<n && arr[child + 1] < arr[child])
		{
			child++;
		}
		if (arr[parent] > arr[child])
		{
			Swap(&arr[parent],&arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
	
}

int main()
{
	int arr[] = { 27, 15, 19, 18, 28, 34, 65, 44 };
	int sz=sizeof(arr)/sizeof(arr[0]);	
	AdJustDown(arr,sz,0);
	for (int i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}

}

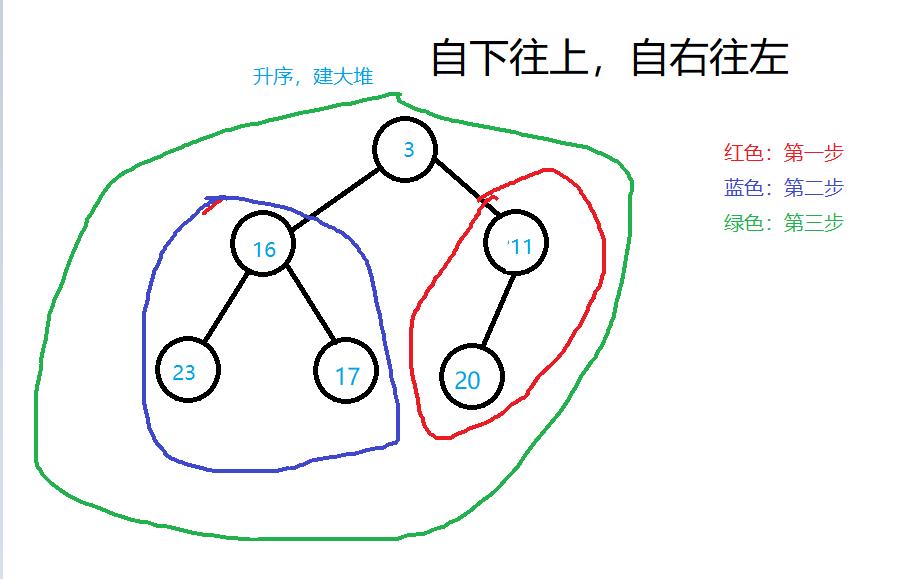
建大堆：
排升序建大堆，排降序建小堆。

1. 建大堆
2. 自下往上，自右往左

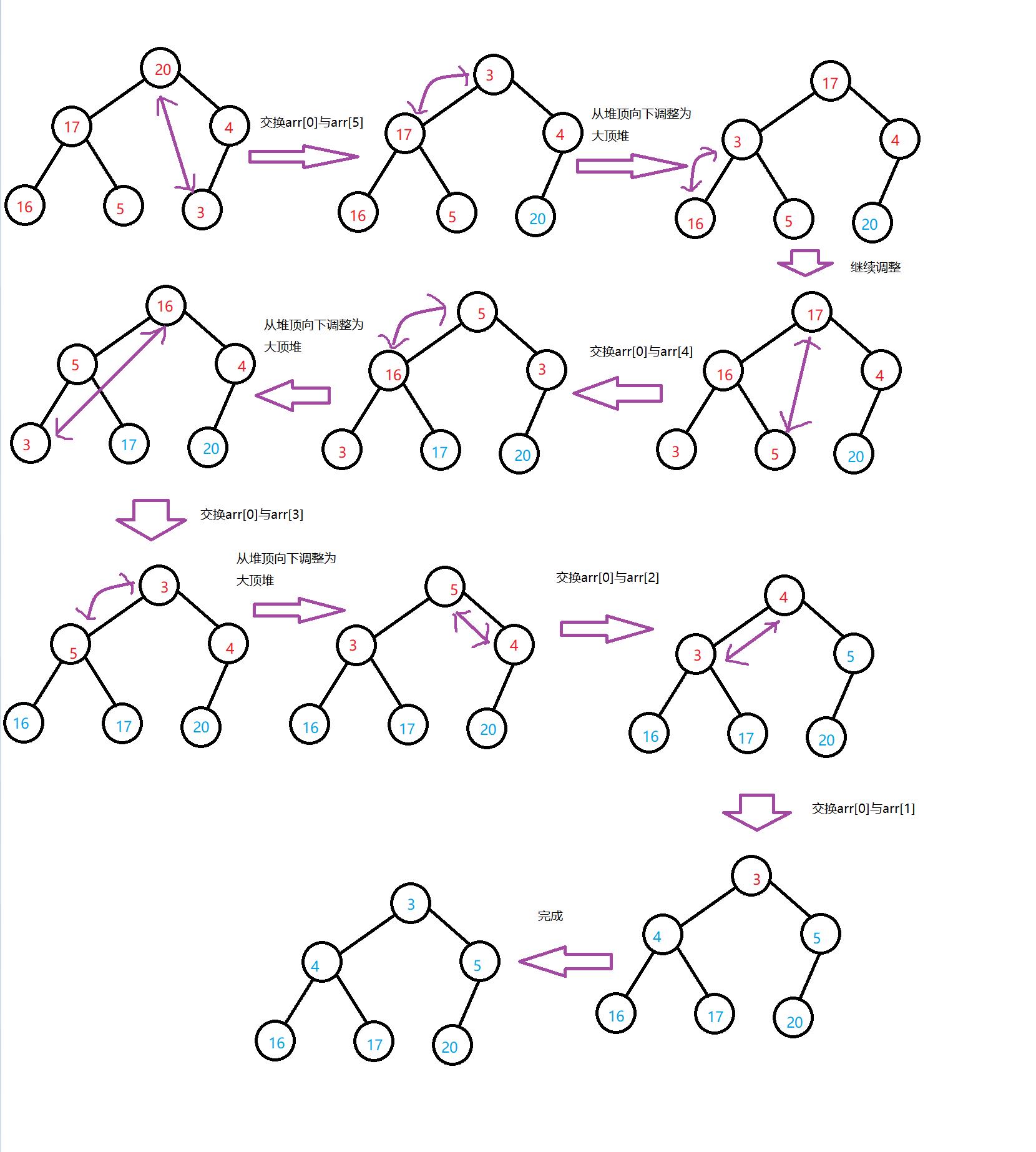
建大堆是自下往上，自右往左

#include<stdio.h>

void Swap(int *p,int *q)
{
	int temp = *p;
	*p = *q;
	*q = temp;
}

void AdJustDown(int *arr,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1<n && arr[child + 1] < arr[child])
		{
			child++;
		}
		if (arr[parent] > arr[child])
		{
			Swap(&arr[parent],&arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
	
}
void HeaqSort(int *arr,int n)
{
	//建大堆，自下往上，自右往左。
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdJustDown(arr, n, i);
	}
	//堆排序
	//int end = n - 1;
	//while (end>0)
	//{
		//Swap(&arr[0],&arr[end]);
		//AdJustDown(arr,end, 0);
		//end--;
	//}
}

int main()
{
	int arr[] = { 27, 15, 11, 18, 28, 4, 65, 44 };
	int sz=sizeof(arr)/sizeof(arr[0]);	
	HeaqSort(arr, sz);
	for (int i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}

}

堆排序：

void HeaqSort(int *arr,int n)
{
	//建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdJustDown(arr, n, i);
	}
	//堆排序
	int end = n - 1;
	while (end>0)
	{
		Swap(&arr[0],&arr[end]);
		AdJustDown(arr,end, 0);
		end--;
	}
	
}

向下调整法时间复杂的：log₂ⁿ
建堆时间复杂度：O(N)
堆排序的时间复杂的：O(N*log₂^N)
建堆如下：
我们用满二叉树来计算，堆的高度为h,假设每层高度为hi,每层节点数为ni,则建堆的时间复杂的为：

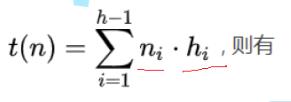
故：时间复杂的为O(N)

二、海量TopK问题

思路一：直接堆排序
时间复杂度：O(Nlog₂^N)
思路二：时间复杂度:O(Nlog₂^k)，空间复杂度O(K)

1. 先把数组中K个数据，建成大堆
2. 然后剩下的N-K个数，跟堆顶的数据比较，如果比堆顶的数据小，则替换堆顶的数据，然后调整堆(这个堆调整是调整前K个的)。
3. 然后堆里面前K个数就是K个小值

 void Swap(int *p,int *q)
{
	int temp = *p;
	*p = *q;
	*q = temp;
}


void AdJustDown(int *arr,int n,int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child+1<n && arr[child + 1] > arr[child])
		{
			child++;
		}
		if (arr[parent] < arr[child])
		{
			Swap(&arr[parent],&arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
	
}
void HeaqSort(int *arr,int n)
{
	//建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdJustDown(arr, n, i);
	}
}

int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize)
{
    int i=k;
    HeaqSort(arr,k);
    for(int k=0;k<arrSize;k++)
    {
       printf("%d ",arr[k]);
    }
    while(i<arrSize)
    {
        if(arr[i]<arr[0])
        {
            Swap(&arr[i],&arr[0]);
            AdJustDown(arr,k,0);
            i++;
        }
        else
        {
            i++;
        }
    }
    int*retarr=(int *)malloc(sizeof(int)*k);
    for(int j=0;j<k;j++)
    {
        retarr[j]=arr[j];
    }
    *returnSize=k;
    return retarr;

}

有错误谢谢提出哦。