蛮力算法求解最近对

Posted 2021-06-07 望北i

蛮力算法最近对

问题描述：
一个包含n个点的集合中，找出距离最近的两个点。
问题分析：
假设所考虑的点是以标准的笛卡尔坐标形式（ x ，y ）给出的，两个点pi = （ xi ，yi ）和 pj =（ xj，yj ）之间的距离是标准的欧几里得距离

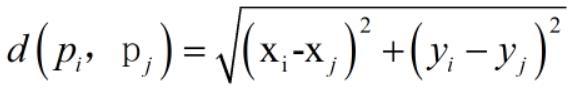
显然求解该问题的蛮力算法应该是：分别计算每一对点之间的距离，然后找出距离最小的那一堆。当然为了提高算法的效率，我们并不希望同一对点计算两次距离，所以我们只考虑 i < j 的那些对（ pi ， pj）。
算法
BruteForceClosePoints( p )
//使用蛮力算法求平面中距离最近的两个点
//输入：一个 n （n >= 2）个点的列表 p ， p1 = （ x1，y1 ），… pn = ( xn, yn )
//输出：两个最近点的距离
d <-- ∞
for i <–1 to n -1 do
for j <-- i + 1 to n do
d <-- min( d, sqrt( xi - xj )² + （ yi - yj )²
return d
算法优化
该算法的基本操作就是计算平方根，，整数的平方根大多是无理数，只能对它们近似求解，而计算这些近似数也不是一件轻松的事。实际上，我们可以避免求平方根，只比较其值的本省。因为如果被开方数越小，它的平方根也越小，平方根函数是严格递增的
核心代码

void FindClosest(Postion P[], int n){
	double min = 10000;
	double  d;
	for(int i = 0; i < n - 1; i++){
		for(int j = i + 1; j < n; j++){
			d = (P[i].x - P[j].x)*(P[i].x - P[j].x) + (P[i].y - P[j].y)*(P[i].y - P[j].y);
			if(d < min){
				min = d;
			}
		}
	}
}

代码实现

/*最近对问题*/ 
#include<stdio.h>

struct Postion{
	double x;
	double y;
}P[100];

void BruteForceClosePoints(Postion P[], int n, int *index1, int *index2){
	double min = 10000;
	double  d;
	for(int i = 0; i < n - 1; i++){
		for(int j = i + 1; j < n; j++){
			d = (P[i].x - P[j].x)*(P[i].x - P[j].x) + (P[i].y - P[j].y)*(P[i].y - P[j].y);
			if(d < min){
				min = d;
				*index1 = i;
				*index2 = j;
				
			}
		}
	}
	printf("第%d个点到%d个点距离最短为%lf", *index1 + 1, *index2 + 1, min);
}

int main(){
	int n, index1,index2;
	printf("请输入点个数\\n");
	scanf("%d", &n);
	for(int i = 0; i < n; i++){
		printf("请输入第%d个点的xy值\\n", i+1);
		scanf("%lf%lf", &P[i].x, &P[i].y);
	} 
	BruteForceClosePoints(P, n, &index1, &index2);
} 

运行结果

代码分析
算法的时间复杂度为 C（n）= O（n²）
虽然加快了算法执行内层循环的速度，但对算法运行时间的提升只是微乎其微的，并不能改变其渐进效率类型。

总结
写博客是为了一是整理所学知识，亲生写代码的经验，而是为了总结经典算法，三是督促自己努力，懂得越多，越知道自己知识的浅薄，四是希望和他人多多交流，有什么不对的地方大佬们多多指点