分治法合并排序

Posted 2021-06-07 望北i

合并排序
合并排序是分治法的应用的一个完美例子。分治法的描述讲解，对于一个需要排序的数组 A[0… n-1],合并排序把他们一分为二：A[0…[n/2]-1] 和 A[0…[n/2]-1] ，并对每个数组递归排序，然后把这两个排好的子数字合并为一个有效数组。

分治过程算法
MergeSort（ 0 ， n - 1）
//递归调用mergesort来对数组划分
//输入：数组排序元素的开始下表和结束下表
//输出升序排列的数组
if( c < d)
mid <–( c + d) /2
MergeSort (c,mid) //左边分治
MergeSort (mid+1, d) //右边分治
Merge ( c, mid, d) //每出栈一次调用一次排序
核心代码

void MergeSort(int c, int d){     //将其全部压栈，然后出栈的时候调用merge函数 
	if(c < d){        //控制递归次数 
		int mid = (c + d) / 2;
		printf("c = %d, d = %d, mid = %d\\n", c, d, mid);//查看每次递归调用时的 c，mid，d，的值便于理解 
		MergeSort(c, mid);     //左边分治 
		MergeSort(mid + 1, d);  //右边分治 
		Merge(c, mid, d);        //每出栈一次被调用一次的 
	}
}

合并算法
Merge(low,mid,high,a[n],b[n])
i <–low
j <–mid + 1
k <–low
while i <= mid and j <= q do
if a[i] < a[j]
b[k++] <-- a[i++]
else
b[k++] <-- a[j++]
while i <= mid
b[k++] <-- a[i++]
while j <= high
b[k++] <-- a[j++]
for i<–low to high
a[i] <-- b[i]
代码实现

void Merge(int low, int mid, int high){
	int i = low;
	int j = mid + 1;
	int k = low;
	while(i <= mid && j <= high)        
		if(a[i] < a[j])
			b[k++] = a[i++];
		else
			b[k++] = a[j++];
	while(i <= mid)                    
			b[k++] = a[i++];
	while(j <= high)                  
			b[k++] = a[j++];
	for(i = low; i <= high; i++){     //将零时数组的值赋值给原数组 
			a[i] = b[i];
		}
} 
voi

例题：
用合并算法对数列8，3，2，9，7，1，5，4进行排序操作
分析
首先对该数列进行分治两两分为一组，先将8，3，分为一组，2，9分为一组7，1分为一组，5，4，分为一组，将这些组里元素进行排序，再将8，3和2，9这两组组内排好序元素排序，7，1和5，4进行同样操作，最后将8，3，2，9和7，1，5，4这两组排序，所有操作应该在零时数组中，最后将零时数组的元素拷贝到原数组中去
代码实现

/*用合并排序算法对
8，3，2，9，7，1，5，4
进行排序*/

#include<stdio.h>
#define n 8
	int a[n] = {8, 3, 2, 9, 7, 1, 5, 4};    //原数组 
	int b[n];                       //零时数组 

void Merge(int low, int mid, int high){
	int i = low;
	int j = mid + 1;
	int k = low;
	while(i <= mid && j <= high)         // 
		if(a[i] < a[j])
			b[k++] = a[i++];
		else
			b[k++] = a[j++];
	while(i <= mid)                    // 
			b[k++] = a[i++];
	while(j <= high)                  // 
			b[k++] = a[j++];
	for(i = low; i <= high; i++){     //将零时数组的值赋值给原数组 
			a[i] = b[i];
		}
} 
void MergeSort(int c, int d){     //将其全部压栈，然后出栈的时候调用merge函数 
	if(c < d){        //控制递归次数 
		int mid = (c + d) / 2;
		printf("c = %d, d = %d, mid = %d\\n", c, d, mid);//查看每次递归调用时的 c，mid，d，的值便于理解 
		MergeSort(c, mid);     //左边分治 
		MergeSort(mid + 1, d);  //右边分治 
		Merge(c, mid, d);        //每出栈一次被调用一次的 
	}
}

int main(){
	printf("排序前的序列 \\n");
	for(int i = 0; i < n; i++){           //排序前的序列 
		printf("%-2d", a[i]); 
	} 
	printf("\\n");
	MergeSort(0, n-1);
	printf("排序后的序列 \\n");
	for(int i = 0; i < n; i++){
		printf("%-2d", a[i]);
	}
}
 

代码分析

递归调用的过程其实就是压栈和出栈的操作，并且每递归一次，调用一次Merge排序函数，用画图来演示一下

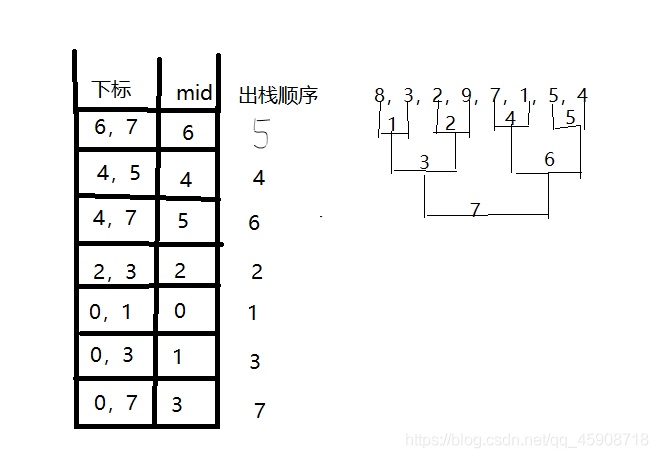
该算法的时间复杂度为O(nlogn)
该算法是稳定的，不会改变数据的大小的相对位置。

总结
写博客是为了一是整理所学知识，亲生写代码的经验，而是为了总结经典算法，三是督促自己努力，懂得越多，越知道自己知识的浅薄，四是希望和他人多多交流，有什么不对的地方大佬们多多指点