分治法快速排序

Posted 2021-06-07 望北i

快速排序
快速排序是按照元素的值对他们进行划分。划分是对给定数组中的元素的重新排列,使得A[s]左边的元素都小于等于A[s],而所有A[s]右边的元素都大于等于A[s]。
A[0]…A[s-1] A[s] A[s+1]…A[n-1]
建立了一个划分后，A[s]已经位于它在有序数组中的最终位置，接下来我们对A[s]前和A[s]后的子数组分别进行排序（使用同样的方法），注意在快速排序中，算法的主要工作在于划分阶段，而不需要再去合并子问题的解了
快速排序的划分算法
QuickSort(A[l…r])
//用QuickSort对子数组进行排序
//输入：数组A[0…n-1]中的子数组A[l…r],由左右下标l和r定义
//输出：非降序排列的子数组A[l…r]
if l < r
s <–GetStandard(A[l…r]) //s是每次分裂位置
QuickSort(A[l…s-1])
QuickSort(A[s+1…r])
代码实现

void QuickSort(int a[], int low, int high) {     //开始默认基准为 low 
	if(low < high) {     //分段下表 
	printf("low  = %d, high = %d \\n", low, high);
		int standard = GetStandard(a, low, high);   //递归调用排序 
		QuickSort(a, low, standard - 1);   //左边排序 
		QuickSort(a, standard + 1, high);  //右边排序		 
	}
} 

快速排序的排序过程

int GetStandard(int a[], int i, int j){   //基准数据 
	int key = a[i];
	while(i < j) {
		while(i < j && a[j] >= key) {   //因为默认基准是从左边开始的，所以从右边开始比较 
			j--;             //当队尾的元素大于基准数据时，就一直向前挪动 j 指针 
		}
		if(i < j) {
			a[i] = a[j];    //当找到比 a[i] 小的时，就把后面的值 a[j] 赋值给它 
		}
		while(i < j && a[i] <= key){
			i++;    //当找到比 a[j] 大的时，就把前面的值 a[i] 赋值给它 
		}
		if(i < j) {
			a[j] = a[i];
		} 
	}               //跳出循环时，i 和 j 的值相等，此时 i 或 j 就是 key 的正确索引位置  
	a[i] = key;    //把基数数据赋给正确位置 
	return i; 
} 

例题
用分治法对 5, 3, 1, 9, 8, 2, 4, 7 进行快速排序

#include<stdio.h>
int GetStandard(int a[], int i, int j){   //基准数据 
	int key = a[i];
	while(i < j) {
		while(i < j && a[j] >= key) {   //因为默认基准是从左边开始的，所以从右边开始比较 
			j--;             //当队尾的元素大于基准数据时，就一直向前挪动 j 指针 
		}
		if(i < j) {
			a[i] = a[j];    //当找到比 a[i] 小的时，就把后面的值 a[j] 赋值给它 
		}
		while(i < j && a[i] <= key){
			i++;    //当找到比 a[j] 大的时，就把前面的值 a[i] 赋值给它 
		}
		if(i < j) {
			a[j] = a[i];
		} 
	}               //跳出循环时，i 和 j 的值相等，此时 i 或 j 就是 key 的正确索引位置  
	a[i] = key;    //把基数数据赋给正确位置 
	return i; 
} 

void QuickSort(int a[], int low, int high) {     //开始默认基准为 low 
	if(low < high) {     //分段下表 
	printf("low  = %d, high = %d \\n", low, high);
		int standard = GetStandard(a, low, high);   //递归调用排序 
		QuickSort(a, low, standard - 1);   //左边排序 
		QuickSort(a, standard + 1, high);  //右边排序		 
	}
} 

void printf(int a[], int n){
	for(int i = 0; i < n; i++)
		printf("%-3d", a[i]);
}

int main(){
	int a[8] = {5, 3, 1, 9, 8, 2, 4, 7};
	for(int i = 0; i < 8; i++)
		printf("%-3d", a[i]);
	printf("\\n");
	QuickSort(a, 0, 7);
	printf(a, 8); 
	return 0;
} 

运行结果

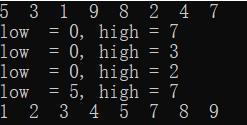
代码分析
利用递归调用树，分析递归调用的过程，调入值是子数字的边界 l 和 r 以及划分的分裂位置 s

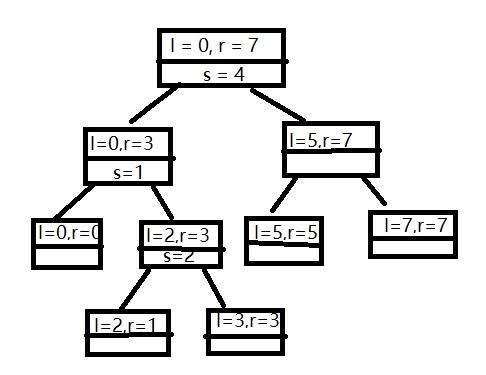
时间复杂度：nlogn
快速排序是不稳定算法

结尾
写博客是为了一是整理所学知识，亲生写代码的经验，而是为了总结经典算法，三是督促自己努力，懂得越多，越知道自己知识的浅薄，四是希望和他人多多交流，有什么不对的地方大佬们多多指点