数据结构-Day_1

Posted 2021-06-07 坏坏-5

文章目录

• 数据结构概述
• • 结构体
• 线性结构
• • 连续存储
  • 离散存储
  • 线性结构的常见应用
  • • 栈
    • 队列
  • 递归

---

文章参考郝斌老师的《数据结构》视频

数据结构概述

• 定义：如何把现实中大量而复杂的问题以特定的数据类型和特定的存储结构保存到主存储器（内存）中，以及在此基础上为实现某个功能（对元素的插入、删除、排序）而执行的相应操作（算法）
• 数据结构：
  • 狭义：数据结构是研究数据存储的问题，数据的存储包括两方面：个体的存储和个体关系的存储
  • 广义：数据结构即包含数据的存储也包含数据的操作，对存储数据的操作就是算法
• 算法：对存储数据的操作，是解题的方法和标准
  • 狭义：算法和数据的存储方式密切相关
  • 广义：算法和数据的存储方式无关
• 衡量算法的标准：
  • 时间复杂度：程序要执行的次数，而并不是执行的时间
  • 空间复杂度：算法执行过程中，所占用的最大内存
  • 难易程度
  • 健壮性

结构体

• 用户根据实际需求，自己定义的复合数据类型
• 结构体变量不能加减乘除，可以互相赋值
• 普通结构体变量和结构体指针变量座位函数传参
• 动态内存分配的空间需要强制类型转换
  • 因为指针型变量只存储首4个字节，需要声明存储变量的类型，才能确定多少个字节表示一个元素
  • malloc可以自动类型转换，即也可以不进行强制转换类型
  • 使用free()可以对动态分配的内存进行释放，动态分配的内存，只能通过手动释放，函数结束，动态分配的内存不会被释放

线性结构

• 所有结点可以用一根线串起来
• 有n个结点，前面只有一个结点，后面只有一个结点
• 线性结构有连续存储（数组）和离散存储（链表）

连续存储

• 数组，每个元素的存储是连续不间断的
• 优点：存取的速度快
• 缺点：事先需要知道数组的长度，需要大块连续的内存，删除插入元素慢，空间有限制

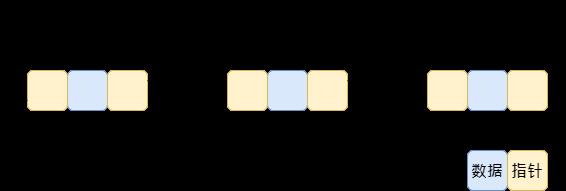
离散存储

• 定义
  • n个结点离散分配，地址不连续
  • 彼此之间使用指针相连
  • 每个结点只有一个前驱结点，只有一个后续结点
  • 首结点没有前驱结点，尾结点没有后续结点
• 优点：插入删除元素快，空间没有限制
• 缺点：存取的速度慢
• 专业术语
  • 首结点：存放第一个有效数据的结点
  • 尾结点：存放最后一个有效数据的结点
  • 头结点：存放第一个存放有效数据结点的指针（地址），即首结点的指针
    • 头结点的数据类型和首结点的数据类型一致
    • 头结点不存放有效数据，存放首结点的指针
    • 头结点的目的是为了方便对链表的操作
  • 头指针：指向头结点的指针变量
  • 尾指针：指向尾结点的指针变量
• 通过一个函数对链表进行处理，只需要知道链表的头指针，可以通过头指针推算出链表的其他所有参数
• 分类
  • 单链表
  • 双链表：每个结点由两个指针域
  • 循环链表：能通过任何一个结点找到其他所有的结点
  • 非循环链表

• 算法：侠义算法是与数据的存储方式密切相关的，广义算法是与数据的存储方式无关
  • 遍历
  • 查找
  • 清空
  • 销毁
  • 求长度
  • 排序
  • 删除结点
  • 插入结点

/*删除结点*/
r = p->pNext;
p->pNetx = r->pNext;
free(r);  //必须要释放内存，防止内存泄露，导致内存越用越少

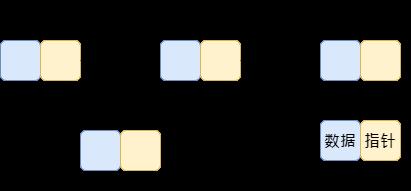
/*插入结点*/
r = p->pNext;
p->pNext = q;
q->pNext = r;

//方法二
q-pNext = p->pNext;
p->pNext = q;

• 泛型：利用某种技术达到的效果：不同的存储方式，所执行的操作一样

【参考链表综合程序】

线性结构的常见应用

栈

• 定义：
  • 可以实现先进后出的存储结构
  • 栈类似箱子，先放进去的最后取出
• 分类：
  • 静态栈
  • 动态栈
• 算法：
  • 出栈：只能出栈最后存入的元素
  • 压栈：栈底的元素只有最后才能出栈
• 应用
  • 函数调用
  • 中断
  • 表达式求值
  • 内存分配
  • 缓冲处理

【参考栈的综合程序】

队列

• 定义：可以实现先进先出的存储结构
• 分类：
  • 链式队列：用链表实现，只能从第一个元素删除，从最后一个元素加入
  • 静态队列：用数组实现，通常必须是循环队列
    • front指向队列的第一个元素，rear指向队列最后一个元素的下一个元素
    • 无论是入队还是出队，front和rear都只能增，不能减，导致用过的内存不能再复用
• 循环队列：
  • 确定一个队列需要两个参数：front、rear
    • 队列初始化中：front和rear都是零
    • 队列非空时：front指向队列的第一个元素，rear指向队列的最后一个有效元素的下一个元素
    • 队列空时：front和rear相等，但值不一定是零
  • 入队列：
    • 将值存入rear指向的位置
    • rear = (rear + 1) % 数组长度
  • 出队列：
    • front = (front + 1) % 数组长度
  • 判断队列是否满
    • 多增加一个标识参数，判断是否等于队列的长度
    • 少用一个元素，front == (rear + 1) % 数组长度成立则满，否则未满
• 队列的应用
  • 所有和时间有关的操作都与队列有关

【参考队列综合程序】

递归

• 一个函数自己直接或间接调用自己
• 当函数在运行期间调用另一个函数时，在运行被调函数之前，需要完成：
  • 将所有的实参、下一个执行的语句的地址传递给被调函数保存
  • 为被调函数的局部变量，包括形参分配存储空间
  • 将控制转移到被调函数的入口
• 被调函数返回主调函数时，需要完成：
  • 保存被调函数的返回结果
  • 释放被调函数所占的存储空间
  • 依照被调函数保存的返回地址，将控制转移到调用函数
• 多个函数互相调用时，遵循先调用先返回的原则，函数之间的信息传递和控制转移必须借助栈来实现，将整个程序运行时所需的数据空间安排在一个栈中，当调用一个函数时，就在栈顶分配一个存储区，进行压栈操作，当一个函数推出时，就释放它的存储区，进行出栈操作，当前运行的函数永远在栈顶位置
• 递归需要满足的条件
  • 递归必须有明确的终止条件
  • 函数处理的数据规模必须是在递减
  • 转化是可解的

例：汉诺塔

• 有三根柱子A、B、C，有n个大小不一样的盘子，每次只能移动一个盘子，并且始终要保证大盘子在下面，下盘子在上面。现在所有盘子都在A上，要求全部移动到C上

# include <stdio.h>

void Hannuota(int n, char A, char B, char C)
{
	if (1 == n)
		printf("编号%d的盘子：%c->%c\\n", n, A, C);
	else
	{
		Hannuota(n - 1, A, C, B);
		printf("编号%d的盘子：%c->%c\\n", n, A, C);
		Hannuota(n - 1, B, A, C);
	}
}

int main(void)
{
	char ch1 = 'A';
	char ch2 = 'B';
	char ch3 = 'C';
	int n;

	printf("请输入要移动的盘子的个数：");
	scanf("%d", &n);

	Hannuota(n, ch1, ch2, ch3);

	return 0;
}

/*伪代码*/
如果只有1个盘子
	直接把1号盘子从A移动到C
否则
	先将A柱子上的n-1个盘子借助C移动到B
	然后直接将A柱子上编号n的盘子移动到C
	最后将B柱子上的n-1个盘子借助A移动都C

/*运行结果*/
请输入要移动的盘子的个数：3
编号1的盘子：A->C
编号2的盘子：A->B
编号1的盘子：C->B
编号3的盘子：A->C
编号1的盘子：B->A
编号2的盘子：B->C
编号1的盘子：A->C
Press any key to continue . . .

---

以上内容均属原创，如有不详或错误，敬请指出。

本文作者： 坏坏

本文链接： https://blog.csdn.net/qq_45668124/article/details/117386248

版权声明： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请联系作者注明出处并附带本文链接！