R实验.7回归分析
Posted 是璇子鸭
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了R实验.7回归分析相关的知识,希望对你有一定的参考价值。
解法并不单一,下列方法带有璇子个人的偏好,因此仅供参考。如有错误,欢迎在评论区斧正!
7.1 为了估计山上积雪融化后对下游灌溉的影响,在山上建立一个观测站,测量最大积雪深度X 与当年灌溉面积Y,测得连续10 年的数据如表7-6 所示:
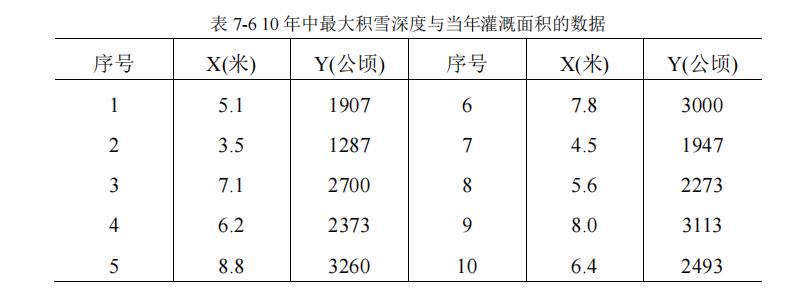
(1)试画出相应的散点图,判断Y 与X 是否有线性关系;
> x <- data$X.米.
> y <- data$Y.公顷.
> plot(x,y)
由散点图,x与y具有一定的线性关系
(2)求出Y 关于X 的一元线性回归方程;
> fit1 <- lm(y~x)
> summary(fit1)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-128.591 -70.978 -3.727 49.263 167.228
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 140.95 125.11 1.127 0.293
x 364.18 19.26 18.908 6.33e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 96.42 on 8 degrees of freedom
Multiple R-squared: 0.9781, Adjusted R-squared: 0.9754
F-statistic: 357.5 on 1 and 8 DF, p-value: 6.33e-08
由fit1的描述统计结果,得y关于x的一元线性回归方程为:
Y
=
364.18
∗
x
+
140.95
Y = 364.18*x + 140.95
Y=364.18∗x+140.95
(3)对方程作显著性检验;
由结果:x系数对应t统计量P值<<0.05,F统计量对应P值小于0.05,即t检验与F检验均通过。同时修正后的拟合优度为0.9754,方程的解释较强,故该模型通过显著性检验。
(4) 现测得今年的数据是X=7 米,给出今年灌溉面积的预测值和相应的区间估计(alpha=0.05)
> predict(fit1,data.frame(x=7),interval='confidence')
fit lwr upr
1 2690.227 2613.35 2767.105
得到今年灌溉面积的预测值为2690.227,相应的区间估计为[2613.35, 2767.105]
7.2 研究同一地区土壤所含可给态磷的情况,得到18 组数据如表7-7 所示,表中X1 为土壤内所含无机磷浓度,X2 为土壤内溶于K2CO3 溶液并受溴化物水解的有机磷,X3 为土壤内溶于K2CO3 溶液但不溶于溴化物水解的有机磷。
(1)求出Y 关于X 的多元线性回归方程
> data7.2 <- read.table('data7.2.txt',header = T)
> fit2 <- lm(Y~X1+X2+X3,data=data7.2)
> summary(fit2)
Call:
lm(formula = Y ~ X1 + X2 + X3, data = data7.2)
Residuals:
Min 1Q Median 3Q Max
-28.349 -11.383 -2.659 12.095 48.807
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 43.65007 18.05442 2.418 0.02984 *
X1 1.78534 0.53977 3.308 0.00518 **
X2 -0.08329 0.42037 -0.198 0.84579
X3 0.16102 0.11158 1.443 0.17098
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 19.97 on 14 degrees of freedom
Multiple R-squared: 0.5493, Adjusted R-squared: 0.4527
F-statistic: 5.688 on 3 and 14 DF, p-value: 0.009227
由回归结果,y关于x的多元线性回归方程为:
Y
=
1.78534
x
1
–
0.08329
x
2
+
0.16102
x
3
+
43.65007
Y = 1.78534x1 – 0.08329x2 + 0.16102x3 + 43.65007
Y=1.78534x1–0.08329x2+0.16102x3+43.65007
(2)对方程做显著性检验
易知x1,x2,x3系数的t统计量对应P值,有且仅有x1系数的对应P值<0.05显著,x2,x3的系数不显著。同时,虽然F统计量对应P值<0.05,但方程修正后的拟合优度只有0.4527,即方程的解释力度较弱。因此,我们还需进行逐步回归分析,来进一步筛选自变量,进而提升方程的解释力度。
(3)对变量做逐步回归分析
> library(MASS)
> stepAIC (fit2, direction = "backward")#向后逐步回归
Start: AIC=111.27
Y ~ X1 + X2 + X3
Df Sum of Sq RSS AIC
- X2 1 15.7 5599.4 109.32
<none> 5583.7 111.27
- X3 1 830.6 6414.4 111.77
- X1 1 4363.4 9947.2 119.66
Step: AIC=109.32
Y ~ X1 + X3
Df Sum of Sq RSS AIC
<none> 5599.4 109.32
- X3 1 833.2 6432.6 109.82
- X1 1 5169.5 10768.9 119.09
Call:
lm(formula = Y ~ X1 + X3, data = data7.2)
Coefficients:
(Intercept) X1 X3
41.4794 1.7374 0.1548
开始时模型包含3个(全部)预测变量,然后每一步中,AIC 列提供了删除一个行中变量后模型的AIC 值,中的AIC 值表示没有变量被删除时模型的AIC。第一步,x2被删除,AIC 从111.27降低到109.32;然后再删除变量将会增加AIC,因此终止选择过程。
向后逐步回归的最终模型为:
Y
=
1.7374
x
1
+
0.1548
x
3
+
41.4794
Y = 1.7374x1 + 0.1548x3 + 41.4794
Y=1.7374x1+0.1548x3+41.4794
逐步回归法其实存在争议,虽然它可能会找到一个好的模型,但是不能保证模型就是最佳模型,因为不是每一个可能的模型都被评价了。为克服这个限制,故我们用全子集回归法来验证一下结果。
library(leaps)
> data1 <- as.data.frame(data7.2[,c("Y", "X1","X2", "X3")])
> leaps <-regsubsets(Y ~ X1 + X2 + X3, data=data1, nbest=4)
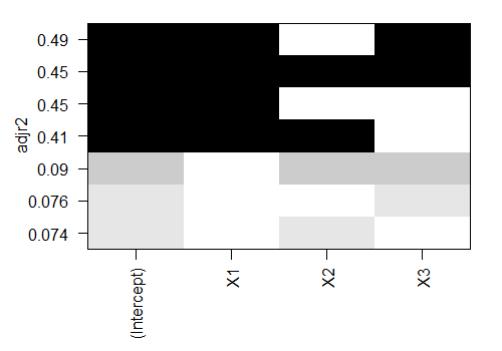
> plot(leaps, scale="adjr2")
图形表明,双预测变量模型(x1和x3)是最佳的模型,与向后逐步回归的结果一致。
7.3 已知如下数据,由表7-8 所示:
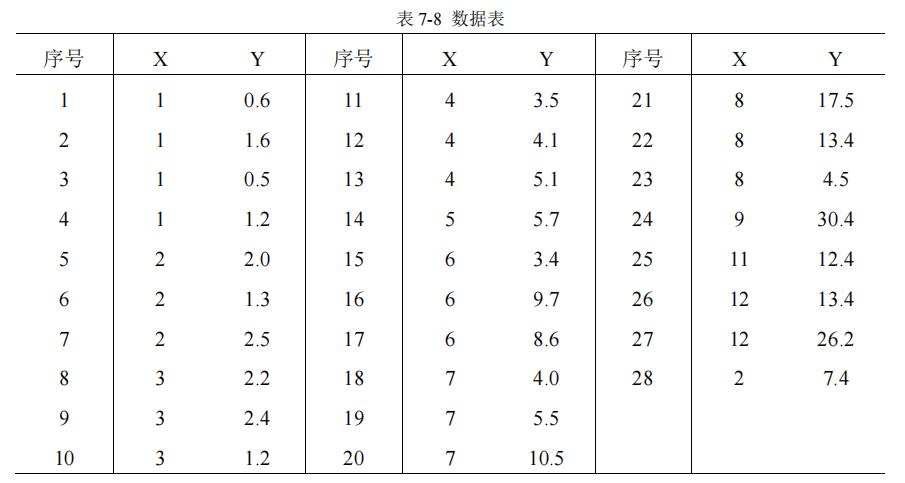
(1)画出数据的散点图,求回归直线
y
=
β
0
^
+
β
1
^
x
y= \\widehat{\\beta_0}+\\widehat{\\beta_1}x
y=β0
+β1
x,同时将回归直线也画在散点图。
> data7.3 <- read.table("data7.3.txt",header = T)
> plot(data7.3$X,data7.3$Y)
> fit3 <- lm(Y~X,data=data7.3)
> abline(fit3)
>
> summary(fit3)
Call:
lm(formula = Y ~ X, data = data7.3)
Residuals:
Min 1Q Median 3Q Max
-7.5173 -1.7928 -0.0147 1.1396 16.6652
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.7228 1.7066 -1.010 0.322
X 1.7175 0.2778 6.184 1.54e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.86 on 26 degrees of freedom
Multiple R-squared: 0.5952, Adjusted R-squared: 0.5797
F-statistic: 38.24 on 1 and 26 DF, p-value: 1.536e-06
回归模型为:
y
=
1.7175
x
–
1.7228
y = 1.7175x – 1.7228
y=1.7175x–1.7228
(2)分析T 检验和F 检验是否通过
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.7228 1.7066 -1.010 0.322
X 1.7175 0.2778 6.184 1.54e-06 ***
F-statistic: 38.24 on 1 and 26 DF, p-value: 1.536e-06
由上面的描述统计,x的t统计量和方程的F统计量对应P值均<<0.05,故T检验和F检验通过。
(3)画出残差(普通残差和标准化残差)与预测值的残差图,分析误差是否是等方差
par(mfrow=c(2,2))
> plot(fit3)
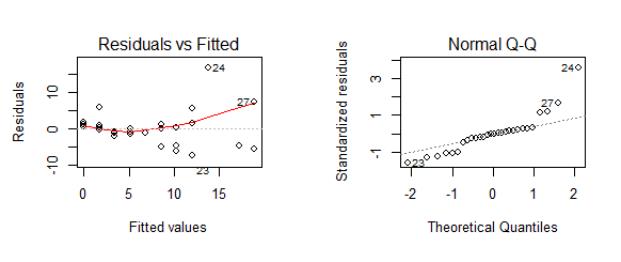
在“残差图与拟合图”(Residuals vs Fitted)中可以清楚的看到一个曲线关系,这暗示着你可能需要对回归模型加上一个二次项。
当预测变量值固定时,因变量成正态分布,则残差值也应该是一个均值为0 的正态分布。正态Q-Q 图(Normal Q-Q,右上)是在正态分布对应的值下,标准化残差的概率。显然,图像表明残差违反了正态性的假设。
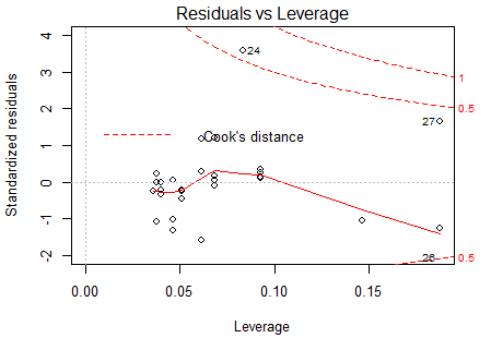
若满足不变方差假设,那么在位置尺度图(Scale-Location Graph)中, 水平线周围的点应该随机分布。由生成图,这里似乎不满足此假设。(略,其和上面的图是一起生成的)
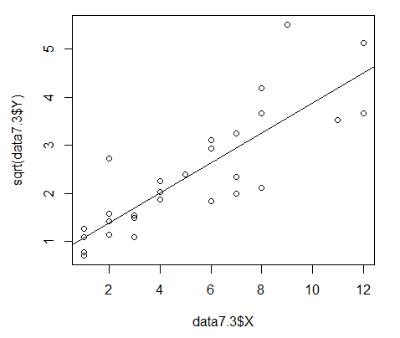
(4)修正模型,对响应变量Y 作开方,再完成(1)-(3)的工作
> plot(data7.3$X,sqrt(data7.3$Y))
> fit4 <- lm(sqrt(Y)~X,data=data7.3)
> abline(fit4)
summary(fit4)
Call:
lm(formula = sqrt(Y) ~ X, data = data7.3)
Residuals:
Min 1Q Median 3Q Max
-1.13695 -0.42839 0.01512 0.29452 1.94385
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.76627 0.24422 3.138 0.0042 **
X 0.31150 0.03975 7.837 2.6e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.6954 on 26 degrees of freedom
Multiple R-squared: 0.7026, Adjusted R-squared: 0.6911
F-statistic: 61.41 on 1 and 26 DF, p-value: 2.598e-08
回归模型为: y ( 1 / 2 ) = 0.3115 x + 0.76627 y^(1/2) = 0.3115x + 0.76627 y(1/2)=0.3115x+0.76627
与前一问原理相同,此时模型通过t检验与F检验,同时拟合优度有了一定的提升。
> par(mfrow=c(2,2))
> plot(fit4)
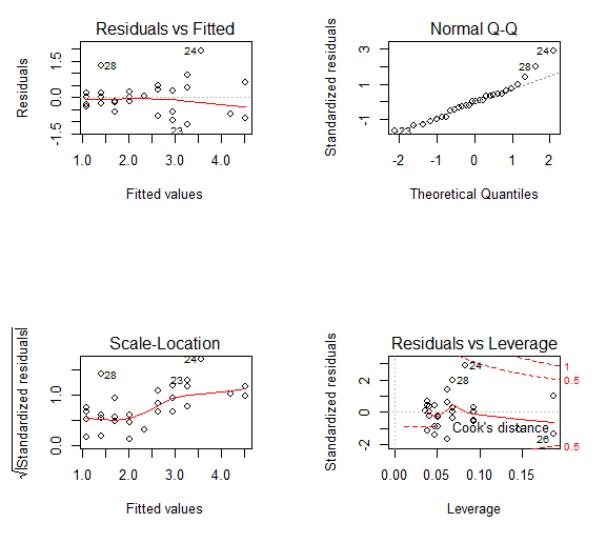
正态Q-Q 图(Normal Q-Q,右上)是在正态分布对应的值下,标准化残差的概率。显然,图像表明残差大致满足了正态性的假设。
而在位置尺度图(Scale-Location Graph)中, 水平线周围的点应该随机分布。该图似乎勉强满足同方差假设。
7.4 一位饮食公司的分析人员想调查自助餐馆中的自动咖啡售货机数量与咖啡销售量之间的关系,她选择了14 家餐馆来进行实验,这14家餐馆在营业额、顾客类型和地理位置方面都是相近的,放在试验餐馆的自动售货机数量从0(这里由咖啡服务员端来)到6 不等,并且是随机分配到每个餐馆的,表7-9 所示的是关于试验结果的数据。
(1)作线性回归模型
data7.4 <- read.table('data7.4.txt',header = T)
> y <- data7.4$售货机数量
> x <- data7.4$咖啡销售量
> fit5 <- lm(y~x)
> summary(fit5)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.44423 -0.23923 0.06288 0.22868 0.44527
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -9.2722554 0.5322309 -17.42 6.94e-10 ***
x 0.0178252 0.0007632 23.36 2.26e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3169 on 12 degrees of freedom
Multiple R-squared: 0.9785, Adjusted R-squared: 0.9767
F-statistic: 545.5 on 1 and 12 DF, p-value: 2.265e-11
由统计结果,模型通过t检验和F检验,且具有较好的解释力度,回归方程式为:
Y
=
0.0178252
∗
x
–
9.2722554
Y = 0.0178252*x – 9.2722554
Y=0.0178252∗x–9.2722554
(2)作多项式回归模型
fit6 <- lm(y ~ x + I(x^2))
> summary(fit6)
Call:
lm(formula = y ~ x + I(x^2))
Residuals:
Min 1Q Median 3Q Max
-0.17759 -0.12396 -0.02883 0.10082 0.20601
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.535e+00 1.622e+00 0.946 0.36425
x -1.542e-02 4.945e-03 -3.118 0.00978 **
I(x^2) 2.484e-05 3.685e-06 6.740 3.2e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1461 on 11 degrees of freedom
Multiple R-squared: 0.9958, Adjusted R-squared: 0.995
F-statistic: 1305 on 2 and 11 DF, p-value: 8.422e-14
同理,模型均通过了t检验与F检验,且具有较好的解释力度。模型表达式为:
Y
=
−
0.01542
x
+
0.00002484
(
x
2
)
+
1.535
Y = -0.01542x + 0.00002484(x^2) + 1.535
Y=−0.01542x+0.00002484(x2)+1.5以上是关于R实验.7回归分析的主要内容,如果未能解决你的问题,请参考以下文章