八皇后问题--递归加回溯

Posted 2021-06-07 我是一颗大萝北

一、问题描述

在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

二、问题分析

由于皇后们是不能放在同一行的， 所以可以去掉“行”这个因素，即第1次考虑把皇后放在第1行的某个位置， 第2次放的时候就不用去放在第一行了。第2次考虑把皇后放在第2行的某个位置，第3次考虑把皇后放在第3行的某个位置，这样依次去递归。每计算1行，递归一次，每次递归里面考虑8列，即对每一行皇后有8个可能的位置可以放。找到一个与前面行的皇后都不会互相攻击的位置， 然后再递归进入下一行。找到一组可行解即可输出，然后程序回溯去找下一组可靠解。

三、怎样判断当前皇后和已有皇后是否发生冲突呢？

• 用一个一维数组来表示相应行对应的列，比如col[i]=j表示第i行的皇后放在第j列。一共有8列，所以我们要让c[r]依次取第1列，第2列……一直到第8列， 每取一次我们就去考虑，皇后放的位置会不会和前面已经放了的皇后有冲突：同行，同列，对角线。
• 由于已经 不会同行了，所以不用考虑同行这一点
• 同列：col[r]==col[j]
• 同对角线：同对角线有两种可能，即主对角线方向和副对角线方向。 主对角线方向满足，行之差等于列之差：r-j=col[r]-col[j]; 副对角线方向满足行之差等于列之差的相反数：r-j=col[j]-col[r]

四、代码框架

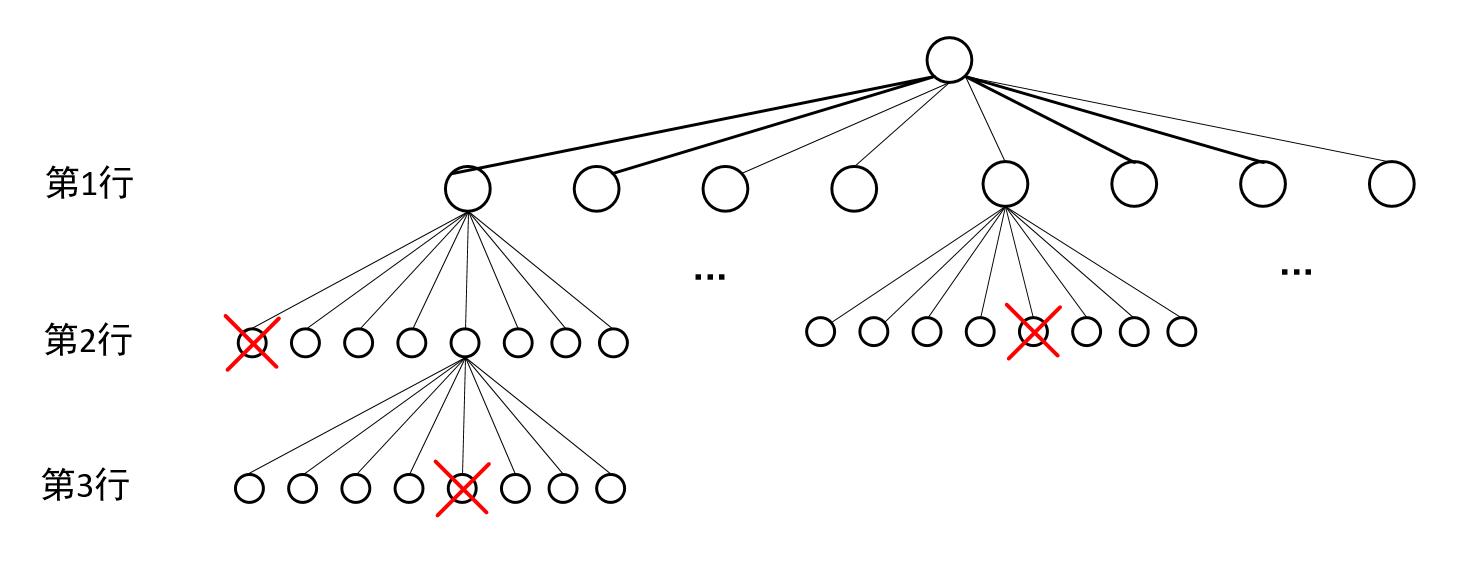
for循环给出8种情况（8列），可以看成一颗树的8个分支。每一个分支节点继续进行递归又出现8个分支，当然有的分支冲突就直接舍弃（如图中红色叉号），到了树的叶子结点就return。

void eight(int line){
	/*--递归出口---*/
	if(line==9){
	。。。
		return;
	}	

	/*---当列不冲突，对角线不冲突时，可以摆放----*/
	for(int j=1;j<=8;j++){  //尝试从第一列开始放 
	。。。	
			eight(line+1);  //递归摆放下一个皇后 
	}
} 
int main(){
	
	eight(1);

	return 0;
}

完整代码如下

#include<bits/stdc++.h>
using namespace std;
int output[9][9];
int col[9];  //1~8行，记录每一行的皇后在哪一列
int cnt=0;

void eight(int line){
	/*--递归出口---*/
	if(line==9){
		cnt++;
		/*输出*/
		for(int i=1;i<=8;i++){
			for(int j=1;j<=8;j++){
				cout<<output[i][j];
			}
			cout<<endl;
		}
		cout<<endl;
		return;
	}	
	
	/*---当列不冲突，对角线不冲突时，可以摆放----*/
	for(int j=1;j<=8;j++){  //尝试从第一列开始放 
		bool colli=false; 
		for(int index=1;index<=line-1;index++){  //看看跟之前的冲不冲突 
			if(j==col[index]||abs(line-index)==abs(j-col[index]))
			{
				colli=true;
		    }
		}
		if(colli==false){  //找到一个和之前皇后都不冲突的位置 
			col[line]=j;  //在这一行摆放一个皇后
			output[line][j]=1;
			eight(line+1);  //递归摆放下一个皇后 
			output[line][j]=0; //回溯！！！！！！！！！！！！！！！！！！！！！！！！！ 
		}
	}
} 
int main(){
	memset(output,0,sizeof(output));
	eight(1);
	cout<<cnt<<"种布局"<<endl; 
	return 0;
}

四、注意手动回溯

递归是可以自己实现回溯的，但是呢由于我们定义了int output[9][9]来输出每一种布局，所以在回溯的时候要求抹掉上一次摆放的皇后。也就是要手动实现这一行

output[line][j]=0; //回溯！！！！！！！！！！！！！！！！！！！！！！！！！ 

如果采用的不是int output[9][9]的方式来输出，那么可以不需要手动回溯，就像下面的代码
早前写的代码了，所以风格和上面的不太一样。

#include <iostream>
#include<stdio.h> 
using namespace std;

int col[20], n=8;//8皇后 
int count=0;//计数多少个布局 
void eightempress(int now);
int main(){
    eightempress(0);
    printf("%d种布局",count);
    return 0;
}
void eightempress(int now){
    if(now == n){
        for(int i=0; i<n; ++i){
            for(int j=0; j<n; ++j){
               if(j == col[i]) printf("1 ");//皇后 
                else printf("0 ");
            }
            cout<<endl;
        }
        cout<<endl;
        count++;
        return;
    }
    for(int i=0; i<n; ++i){
        col[now] = i;//从第一行开始尝试摆放皇后 
        int ok = 1;
        for(int j=0; j<now; ++j)//和之前的now-1个皇后比较 
            if(col[now]==col[j] || abs(now-j)==abs(col[now]-col[j]) ){//列冲突、对角线冲突 
                ok = 0;
                break;
            }
        if(ok) eightempress(now+1);
    }
}