二叉树的递归实现

Posted 2021-06-07 计算机社团

树的基本概念

树的定义

（1）每个元素称为节点（node）。

（2）有一个特定的节点被称为根节点或树根（root）。

树的专有名词

空集合也是树，称为空树。空树中没有节点；

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

节点的度：一个节点含有的子节点的个数称为该节点的度；

叶节点或终端节点：度为0的节点称为叶节点；

非终端节点或分支节点：度不为0的节点；

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；

兄弟节点：具有相同父节点的节点互称为兄弟节点；

树的度：一棵树中，最大的节点的度称为树的度；

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

树的高度或深度：树中节点的最大层次；

堂兄弟节点：双亲在同一层的节点互为堂兄弟；

节点的祖先：从根到该节点所经分支上的所有节点；

子孙：以某节点为根的子树中任一节点都称为该节点的子孙；

二叉树的基本概念

定义

n个结点的有限集合，由一个根结点以及两棵互不相交，分别称为左子树和右子树的二叉树组成

逻辑结构

一个父结点对应两个子结点

基本特征

• 每个结点最多只有两棵子树

• 左子树和右子树次序不能颠倒(有序树) 

二叉树性质

3.对于完全二叉树，若从上到下，从左至右编号，则编号为i的结点，其左孩子结点编号必为2i，其右孩子结点，编号必为2i+1；其双亲结点编号必为i/2(i=1是为根结点)

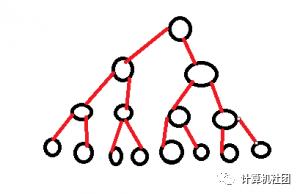
满二叉树

除了根结点只有以外，其他所有结点均长满了两个字结点的二叉树

完全二叉树

除了最后一层外，每一层上的结点数均达到了最大值；在最后一层上只缺少右边诺干结点。

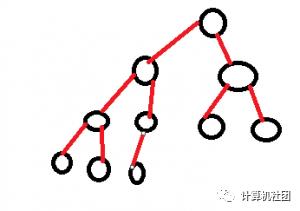
如图为深度为4的完全二叉树，最后一层只有右边结点没有

二叉树的遍历

遍历方法

先序遍历：先访问根，再访问左，再访问右

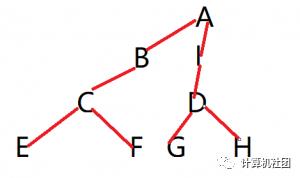
遍历顺序

A->B->C->E->F->I->D->G->H

中旬遍历：先左再根再右

如图：

E->C->F->B->A->G->D->H->I

后序遍历：先左再右再根

如图：

E->F->C->B->G->H->D->I->A

代码实现

二叉树的创建：

struct tree{
    char data;
    tree* lchild;
    tree* rchild;
}

C

Copy

二叉树的初始化：

//递归方法
void create(btnode* &T){
    char c;
    scanf("%c",&c);
    if(c=='/')
        return;
    T=new btnode;
    T->data=c;
    T->lchild=NULL;
    T->rchild=NULL;
    create(T->lchild);
    create(T->rchild);
}

C

Copy

输入'/'表示当前结点为空跳出当前递归；

二叉树的先序遍历递归输出：

void printtree(btnode*T){
    if(T)
    {
        cout<<T->data;
        printtree(T->lchild);
        printtree(T->rchild);
    }
}

C

Copy

以上图先序遍历为例，依次输入

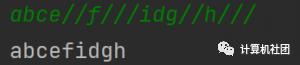
输出按照先序遍历的结果。

如果想进行中旬遍历或者后续遍历，只需要改变T->lchild和T->rchild的顺序即可。

二叉树中序遍历递归输出：

//中序遍历
void printbeettree(btnode*T){
    if(T)
    {
        printtree(T->lchild);
        cout<<T->data;
        printtree(T->rchild);
    }
}

C

Copy

二叉树的后序遍历输出

//后续遍历输出
void printendtree(btnode*T){
    if(T)
    {
        printendtree(T->lchild);

        printendtree(T->rchild);
        cout<<T->data;
    }
}

C

Copy

计算二叉树的结点个数

void numbers_of_node(btnode* T,int &count){
 if(T)
 {
 ++count;
 numbers_of_node(T->lchild,count);
 numbers_of_node(T->rchild,count);
 }
} 

C

Copy

递归计算结点个数并赋值给count。

求二叉树深度

int depth(btnode* T){
 int leftlen,rightlen;
 if(T==NULL)
 return 0;
 else
 {
  leftlen=depth(T->lchild)+1;
  rightlen=depth(T->rchild)+1;
 }
 if(leftlen>rightlen)
 return leftlen;
 return rightlen;
}

C

Copy

完整代码

#include<bits/stdc++.h>
using namespace std;
struct btnode{
    char data;
    btnode* lchild;
    btnode* rchild;
};
//递归方法
void create(btnode* &T){
    char c;
    scanf("%c",&c);
    if(c=='/')
        return;
    T=new btnode;
    T->data=c;
    T->lchild=NULL;
    T->rchild=NULL;
    create(T->lchild);
    create(T->rchild);
}

//abce//f///idg//h///
void printtree(btnode*T){
    if(T)
    {
        cout<<T->data;
        printtree(T->lchild);
        printtree(T->rchild);
    }
}
//中序遍历
void printbeettree(btnode*T){
    if(T)
    {
        printbeettree(T->lchild);
        cout<<T->data;
        printbeettree(T->rchild);
    }
}
//后续遍历输出
void printendtree(btnode*T){
    if(T)
    {
        printendtree(T->lchild);

        printendtree(T->rchild);
        cout<<T->data;
    }
}

void numbers_of_node(btnode* T,int &count)//计算二叉树中结点个数，赋值给count{
    if(T)
    {
        ++count;
        numbers_of_node(T->lchild,count);
        numbers_of_node(T->rchild,count);
    }
}
void leaf(btnode* T,int &count)//求叶子节点个数{
    if(T)
    {
        if(T->lchild==NULL&&T->rchild==NULL)
            count=count+1;
        leaf(T->lchild,count);
        leaf(T->rchild,count);
    }
}
int main(){
    btnode*tree=new btnode;
    tree=NULL;
    create(tree);
    cout<<"先序遍历结果：";
    printtree(tree);
    cout<<endl<<"中序遍历结果：";
    printbeettree(tree);
    cout<<endl<<"后序遍历输出";
    printendtree(tree);
    int a=0;
    leaf(tree,a);
    cout<<endl<<"子节点个数"<<a<<endl;

    return 0;
}

END

编辑：田晶