每日一题 | day09（另类加法 | 走方格的方案数）

Posted 2021-06-07 WhiteShirtI

选择题

1、fun(21)运行结果是()

int fun(int a){
	a^=(1<<5)-1;
	return a;
}

A 10
B 5
C 3
D 8
正确答案 A：在等号左边，(1<<5)为1左移5位，1变成100000。再减去1，为11111,。此时等号右边是a^，a为21，转换成二进制就是10101，两者进行异或，就是相同为0，不同为1。结果为01010，转为10进制就是10

2、以下程序的输出结果是：

#include <iostream>
using namespace std;
void func(char **m){
	++m;
	cout<<*m<<endl;
}
int main(){
	static char *a[]={"morning", "afternoon", "evening"};
	char **p;
	p=a;
	func(p);
	return 0;
}

A afternoon
B 字符o的起始地址
C 字符o
D 字符a的起始地址
正确答案 A：字符串就是地址，*m就是整个字符串，**m就是这个字符串的第一个字母

编程题

题目1：

题解思路：
两个数字的相加可以分为两步，第一步是求两个数字相加后当前二进制为的值，第二步为求两数字相加后的进位值。最后让他们两继续相加，直到有一方为0即表示相加结束，我们举个例子，1+3=4的例子
0001
0011
相加结果不考虑进位，值为0010
求相加的进位，值为0010
这两个值继续相加
0010
0010
相加结果不考虑进位，值为0000
求相加的进位，值为0100
0000
0100
相加结果不考虑进位，值为0100
求相加的进位，值为0000
此时进位为0，相加结束，最终相加的结果0100=4

代码思路：
相加结果不考虑进位，我们可以通过两数的异或来获取
0001^0011 = 0010
求相加的进位，我们可以通过相遇与左移一位获取
(0001&0011)<<1 = 0001<<1 = 0010
我们可以定义两个变量，一个是用于保存相加结果不考虑进位的值sum，一个用于保存相加后进位的值carry。用一个whlie循环来一直遍历相加，直到进位为0时，相加就结束。此时sum保存的结果就是相加后的答案

代码：

class UnusualAdd {
public:
    int addAB(int A, int B) 
    {
        int sum = 0;
        int carry = 0;
        while (B!=0)
        {
            sum = A ^ B;
            carry = (A & B)<<1;
            A = sum;
            B = carry;
        }
        return sum;
    }
};

题目2：

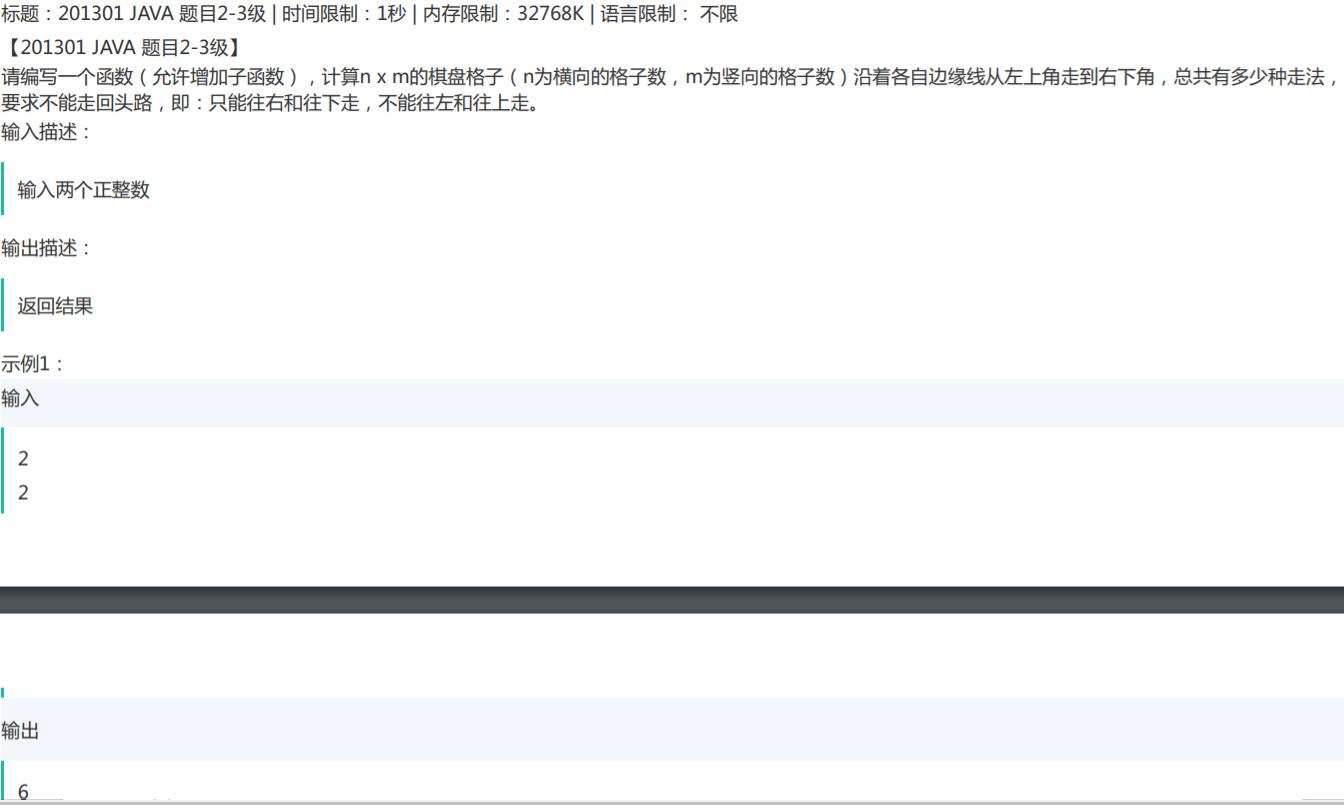
解题思路：
我们读懂这道题后可以将其转换为右下角向左上角走，只能向上走或者向下走或者向上走，我们可以画图来理解

我们知道走法只能向上走或者向左走，我们可以将紫色的走法的方式次数，分解为紫色上一个格子的走法方式次数+紫色左一个格子的走法方式次数，因为要走到红色目的地，就必须经过这两个格子的其中一个，也就得必须经过上一个格子或者左一个格子。没有其他方式可以走到

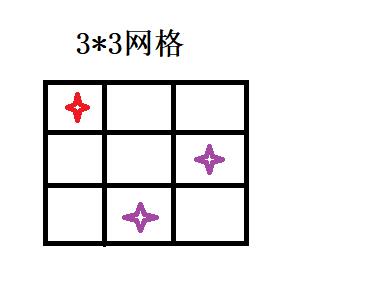
我们再按分解原理，再将这两个格子继续分解

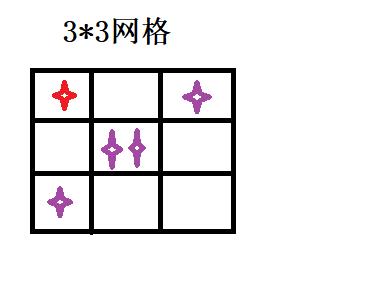
此时我们发现有两格子走到了上边界和下边界，当走到边界也就是只有一种方法了，就是只能一直向上走或者一直向左走。就记录这两次的走法。我们再继续分解

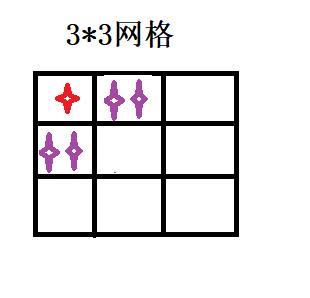
此时有4种到达边界，格各自都有一种方式走到目的地，也就是共有4种，加上上次记录的2中，一共就有6种方式
代码思路：
只要将左下角网格的位置分解为上一个格子和做一个格子进行递归，结束条件为遇到边界，也就是有行或者列为0即走到边界，就返回1，也就是唯一的方式
代码：

#include <iostream>
using namespace std;

int pathNum(int n, int m)
{
    if (n == 0 || m == 0)
        return 1;
    return pathNum(n - 1, m) + pathNum(n, m - 1);
}

int main()
{
    int n, m;
    while (cin >> n >> m)
    {
        cout << pathNum(n, m) << endl;
    }
    return 0;
}