每日一题 | day17（杨辉三角的变形 |超长正整数相加）

Posted 2021-06-07 WhiteShirtI

选择题

1、以下代码执行之后ptr指向的内容是？

char *ptr;
char myString[] = "abcdefg";
ptr = myString;
ptr += 5;

A Compiler error
B f
C efg
D defg

正确答案 B：*ptr是一个指向一个字符的指向，所以只能指向一个字符

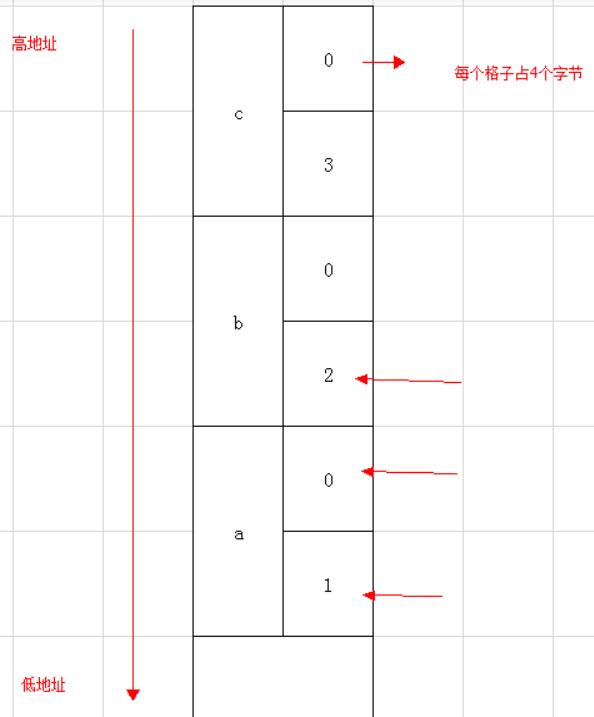
2、假设在一个 32 位 little endian 的机器上运行下面的程序，结果是多少？

#include <stdio.h>
int main(){
	long long a = 1, b = 2, c = 3;
	printf("%d %d %d\\n", a, b, c);
	return 0;
}

A 1,2,3
B 1,0,2
C 1,3,2
D 3,2,1
正确答案 B： printf()是一个库函数，C，C++中函数的参数是从右往左入栈的；栈的生长方向是从高往低的小端模式是低位存储在低字节；%d格式输出的是4个字节大小，而long long为8个字节

编程题

题目1：

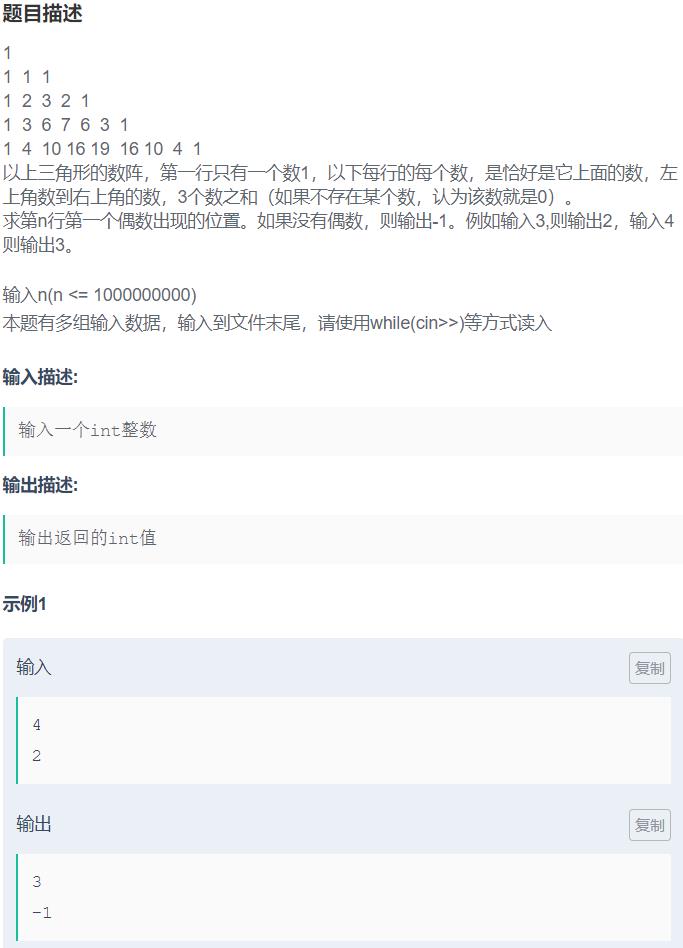
解题思路：
根据题目要求将杨辉三角的变形存储在一个二维数组中。然后再第n行遍历查找第一个偶数。下面我们来看看如何写出杨辉三角的变形。
杨辉三角的变形：第一行只有一个数1，以下每行的每个数，是恰好是它上面的数，左上角数到右上角的数，3个数之和（如果不存在某个数，认为该数就是0）
我们把杨辉三角的变形的样子画出来

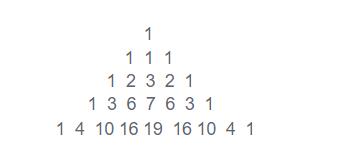
特殊元素：第一个元素和倒数第1个元素都为1，第二个元素为上一行的同列元素+上一行同列后一列元素。倒数第二个元素为上一行同列前一列元素+上一行同列前两列元素
其他元素都为上一行同列的前一列，前二列和同列元素的和

代码：

#include<iostream>
#include <vector>
using namespace std;

int findIndex(int n)
{
    int m = 2 * n - 1;//最后一行的元素取决矩阵的大小
    //二维数组：有n行，其中每行右m个元素，初始值都为0
    vector<vector<int>> vv(n, vector<int>(m, 0));
    vv[0][0] = 1;
    for (int i = 1; i < n; ++i)
    {
        vv[i][0]  = vv[i][2 * i] = 1;//第一个元素和最后元素元素都为1
        for (int j = 1; j < 2 * i; ++j)
        {
            if (j == 1)//第二个元素
                vv[i][j] = vv[i - 1][j - 1] + vv[i - 1][j];
            else if (j == 2*i - 1)//倒数第二个元素
                vv[i][j] = vv[i - 1][j - 1] + vv[i - 1][j - 2];
            else//其他普通元素
                vv[i][j] = vv[i - 1][j - 1] + vv[i - 1][j - 2] + vv[i - 1][j];
        }
    }
    
    for (int k = 0; k < m; ++k)
    {
        if (vv[n - 1][k] % 2 == 0)
            return k + 1;
    }
    return -1;
}

int main()
{
    int n, index;
    while (cin >> n)
    {
        index = findIndex(n);
        cout << index <<endl;
    }
}

投机取巧方案(不推荐)：找规律，前2行都不存在返回-1，往下为奇数行则第二个位置为偶数；如果为偶数且是4的倍数则第3个位置为偶数；剩下其他都是第4个位置为偶数

int findIndex_1(int n)
{
    if (n <= 2)
        return -1;
    if (n % 2 == 1)
        return 2;
    if (n % 4 == 0)
        return 3;
    else
        return 4;
}

题目2

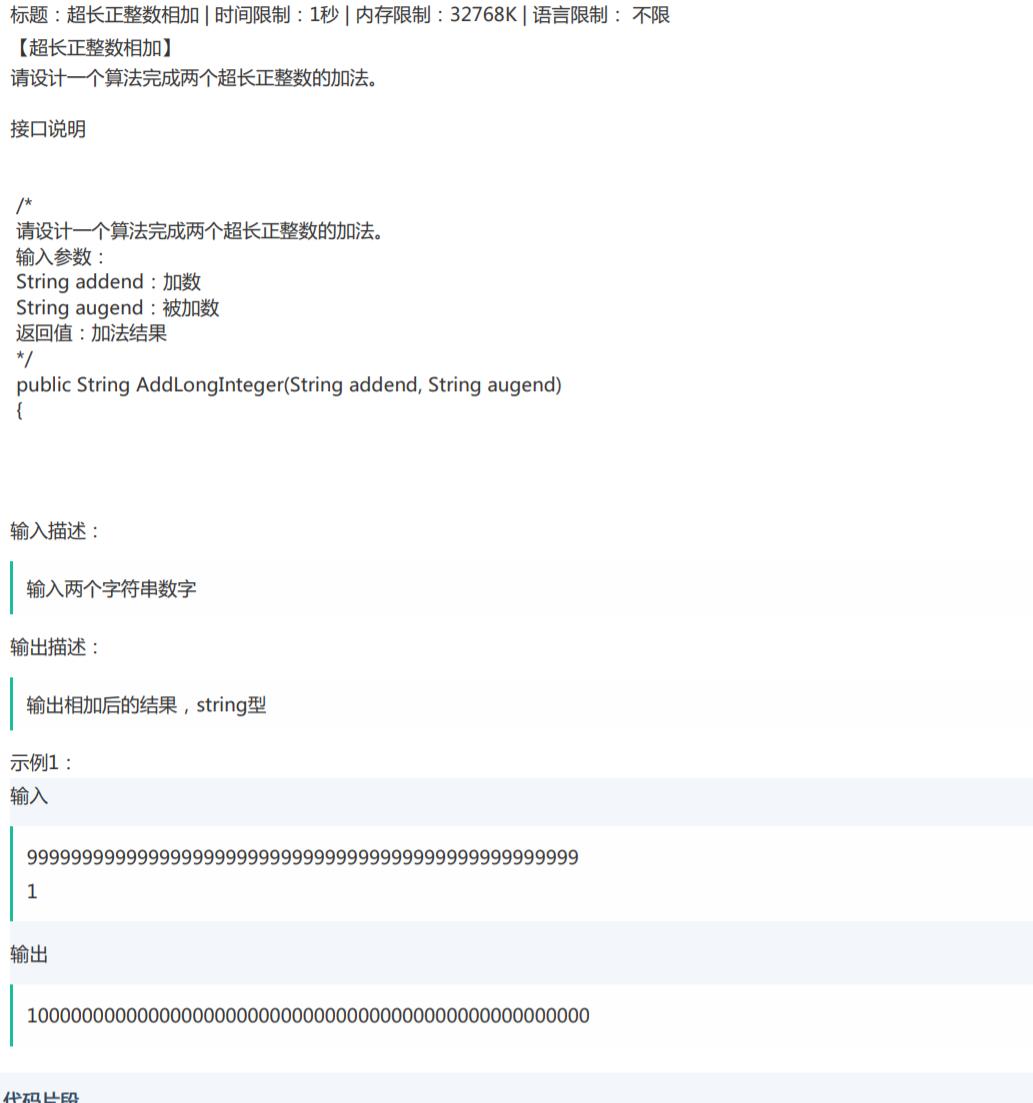
题解思路：
让两个数都从各自长度-1的位置开始相加，也就是个位开始相加。定义一个step变量用于记录上一位相加是否存在进位，进位最大只能为1。只要有一个数没遍历完，就要继续遍历相加。如果有一个遍历完了，设它的值为0，也就是该位的值为未遍历完的数的当前位+0即可。当前位和sun为两个数当前位的值加上进位。如果和大于9表示存在进位，设置step为1，sum -=10。如果小于10表示不存在进位，置step为0。定义一个保存结果的类型为string的res变量，保存每一位计算的结果。循环遍历完后要判断是否还存在进位，存在进位就加在res后面即可。最后反转整个res就为两数相加的结果
代码：

#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
string addLongInteger(string& str1, string& str2)
{
	string res = "";
	int idx1 = str1.size() - 1;
	int idx2 = str2.size() - 1;
	int step = 0;
	while (idx1 >= 0 || idx2 >= 0)
	{
		int left = 0, right = 0;
		if (idx1 >= 0)
			left = str1[idx1--] - '0';
		if (idx2 >= 0)
			right = str2[idx2--] - '0';
		int sum = left + right + step;
		if (sum > 9)
		{
			step = 1;
			sum -= 10;
		}
		else
			step = 0;
		char c = sum + '0';
		res += c;
	}
	if (step == 1)
		res += '1';
	reverse(res.begin(), res.end());
	return res;
}
int main()
{
	string str1, str2;
	while (cin >> str1 >> str2)
	{
		cout << addLongInteger(str1, str2) << endl;
	}
	return 0;
}