每日一题 | day26（变态跳台阶 | 快到碗里来）

Posted 2021-06-07 WhiteShirtI

选择题

1、在单处理器系统中，如果同时存在有12个进程，则处于就绪队列中的进程数量最多为（）
A 1
B 9
C 10
D 11
正确答案 D：在单处理器中，只有一个进程才能运行，也就是必须有一个进程运行，所以就绪队列中进程数量最多为11个

2、下列选项中，会导致进程从执行态变为就绪态的事件是（）。
A 执行 P(wait)操作
B 申请内存失败
C 启动 I/O 设备
D 被高优先级进程抢占

正确答案 D：被高优先级进程抢占，进程会由执行态变为就绪态。ABC三项，程序由于缺少资源而由执行态转为阻塞态。

3、在一个文件被用户进程首次打开的过程中，操作系统需做的是 （）
A 将文件内容读到内存中
B 将文件控制块读到内存中
C 修改文件控制块中的读写权限
D 将文件的数据缓冲区首指针返回给用户进程

正确答案 B：

4、下列措施中，能加快虚实地址转换的是 （）
1增大快表（TLB） 2让页表常驻内存 3增大交换区
A 仅1
B 仅2
C 仅1,2
D 仅2,3

正确答案 C：

5、一个进程的读磁区操作完成后，操作系统针对该进程必做的是 （）
A 修改进程状态为就绪态
B 降低进程优先级
C .进程分配用户内存空间
D 增加进程的时间片大小

正确答案 A：

编程题

题目1：

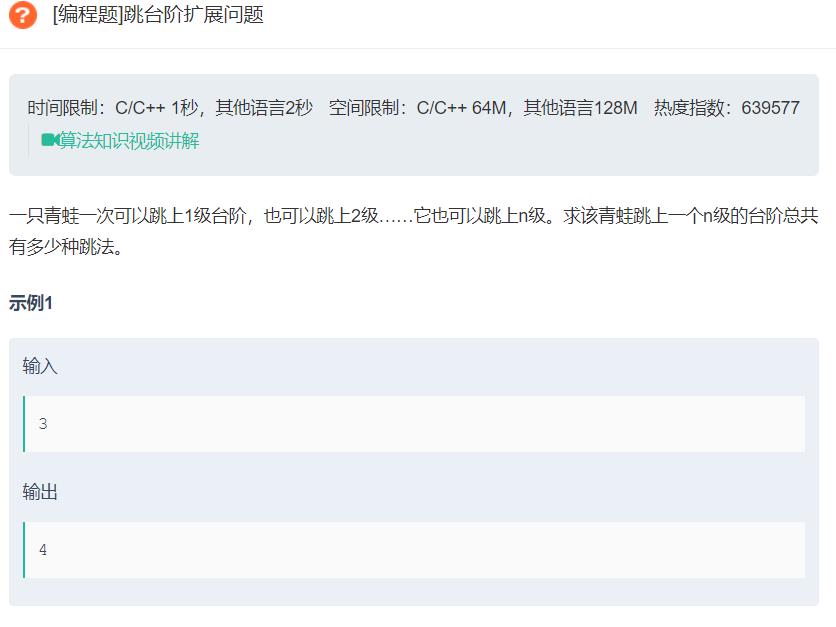
题解思路：
这道题和之前青蛙跳台阶不一样，之前的普通青蛙只能跳一个台阶或者两个台阶，使用斐波那契数列就可以解决，而这个变态青蛙不一样，多少个台阶都可以跳。这时候问题就没那么简单了。这道题可以使用动态规划来解决。

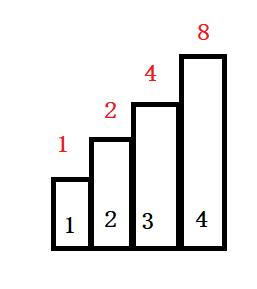
直接说结论，我们可以看出，除了第一个台阶，后面三个台阶都是前n-1个台阶跳法之和+1。我们来分析一下为什么是这样子，要想跳到第二个台阶，有两种办法，第一种就是直接跳两个台阶就到台阶2；第二种是先跳到台阶1，再跳1格就可以跳到台阶2。再来看看跳到台阶三的方案，一共有3种方案，第一种一下跳3个台阶，直接到台阶3；第二种是先跳到台阶1，再跳2个台阶就到台阶3；第三种是先跳到台阶2，再跳到1个台阶就到台阶3。以此类推，跳到台阶4就有4种方案。我们用cnt表示跳法个数，在跳到台阶4种，第一种方案只有一种跳法cnt=1，第二种方案就是跳到台阶1，再跳到台阶4，而跳到台阶1只有1种跳法，所以cnt+1=2；第三种方案就是先跳到台阶2，再跳2个台阶就到台阶4，而跳到台阶2有2种方案，所以cnt+2=4；第四种是先跳到台阶3，再跳1个台阶就到台阶4。而跳到台阶3有4种方案，所以cnt+4=8。
**代码思路：**我们可以定义一个一维数组，并初始化为1，这个1代表的是每跳到n个台阶的第一种跳法，也就是一次性跳n个台阶。定义两个for循环，第一个for循环就是计算每个台阶的方案数，第二个for循环就是计算第i个台阶的次数，也就是累加0到i台阶的方案数

代码：

class Solution {
public:
    int jumpFloorII(int number) {
        vector<int> vec(number, 1);
        for (int i = 1; i < number; ++i)
        {
            for (int j = 0; j < i; ++j)
                vec[i] += vec[j];//累加前i个台阶的跳法
        }
        return vec[number-1];
    }
};

题目2：

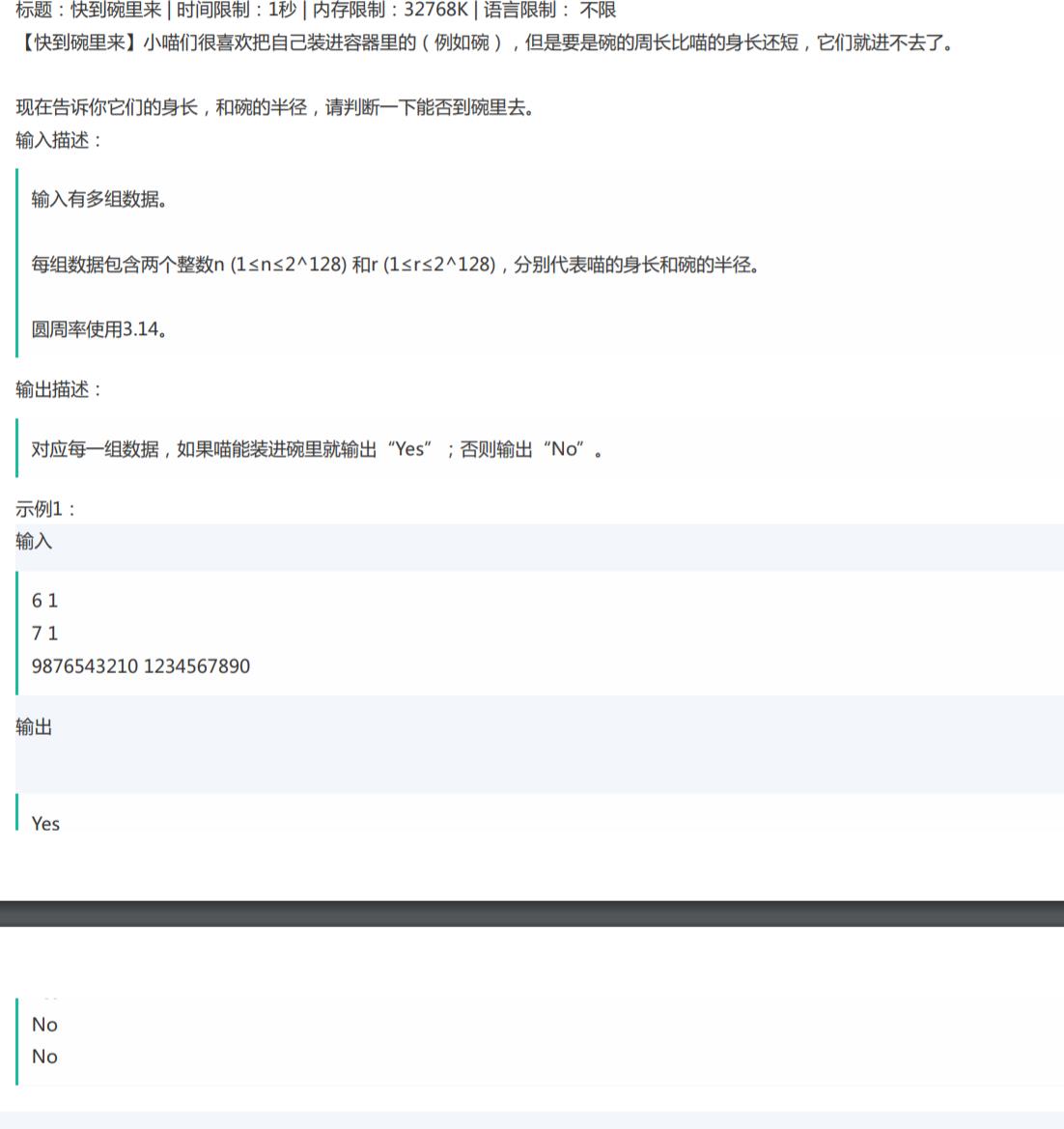
题解思路：这道题简单，只需要注意两个点，第一个就是需要使用浮点数，第二个是题目给出的数字非常大，最大有2^128，所以必须使用double

代码：

#include <iostream>
#include <vector>
using namespace std;
int main()
{
	double n;
	double r;
	while (cin >> n >> r)
	{
		double c = 2 * 3.14 * r;
		if (c >= n)
			cout << "Yes" << endl;
		else
			cout << "No" << endl;
	}
	return 0;
}