5.9拉普拉斯矩阵的谱分解，谱图卷积，图卷积演变过程

Posted 2021-06-07 炫云云

文章目录

• • 拉普拉斯矩阵的谱分解
  • 谱图卷积
  • 线性模型
  • 参考

图卷积的核心思想是消息传递，怎么传递，主要依赖与其他节点的关系，具体来说：图中的每个节点通过卷积的形式将消息传递给邻居并接收邻居传来的消息，它们无时无刻不因为邻居和更远的点的影响而改变着自己的状态直到最终的平衡，关系越近的邻居影响越大。怎么定义与邻居的关系，以及怎么传播这是两个关键的问题。直接一点，根据后续的研究可以发现解决这两个问题的关键是： 拉普拉斯矩阵；谱图卷积

为了获得与邻居的关系，我们从连接矩阵，度矩阵入手。下图1，定义了图上的一些基本概念：节点，边，权重，拉普拉斯矩阵等

$$图1$$

详细的图资料，请看： 图01—图的基本概念与模型

图02—存储结构，邻接矩阵，关联矩阵，权矩阵，邻接表，十字链表

为什么要用到拉普拉斯矩阵？下面简单概括了拉普拉斯矩阵的基本性质：

• 拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解），这就和GCN的spectral domain对应上了
• 拉普拉斯矩阵只在中心顶点和一阶相连的顶点上（1-hop neighbor）有非0元素，其余之处均为0
• 通过拉普拉斯算子与拉普拉斯矩阵进行类比

图1中拉普拉斯算子与拉普拉斯矩阵具体的可以看：

5.8 拉普拉斯算子和拉普拉斯矩阵，图拉普拉斯算子推导

补充一下：

1. 矩阵的谱分解，特征分解，对角化都是同一个概念（特征分解_百度百科）
2. 不是所有的矩阵都可以特征分解，其充要条件为n阶方阵存在n个线性无关的特征向量。
3. 拉普拉斯矩阵是半正定对称矩阵（半正定矩阵本身就是对称矩阵，半正定矩阵_百度百科），线代里关于矩阵有三个相关的性质，来，我们复习一下：

• 对称矩阵一定n个线性无关的特征向量
• 半正定矩阵的特征值一定非负
• 对阵矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵。

拉普拉斯矩阵的谱分解

由上可以知道拉普拉斯矩阵一定可以谱分解，且分解后有特殊的形式

$$图2$$
根据5.10 图上的傅里叶变换和逆变换可以得到：

图傅里叶变换： $F({\lambda }_l)=\hat{f}({\lambda }_l)={\sum }_{i=1}^{N}f(i)\ast u_l^{\ast }(i)=U^{T}f$

图傅里叶变换的逆变换： $f=\mathbf{U}{\mathbf{U}}^{-1}f=\mathbf{U}{\mathbf{U}}^{T}f=\mathbf{U}\hat{f}$

带入$x$： 图信号（也是特征${\lambda }_l$ ），就可以得到图2公式2（ $x$ 的图傅里叶变换）和3 （$x$ 的图傅里叶变换的逆变换）

拉普拉斯矩阵是实对称矩阵，实对称矩阵一定可以用正交矩阵进行正交相似对角化，进而得出拉普拉斯矩阵的谱分解：
$$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_N\end{array}\right)U^{-1}=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_N\end{array}\right)U^T$$
$U$ 为特征向量构成的正交矩阵，也就是标椎正交基向量(想象成二维坐标$x_i$的x,y)，而正交矩阵的逆等于正交矩阵的转置： $U^T=U^{-1}$

假定 ${\lambda }_1,\cdots ,{\lambda }_n$ 从小到大排序，其对应的特征向量为 $u_1,\cdots ,u_n$ ，特征值越小，对应的特征向量越平稳，这和傅立叶变换中频率的定义是类似的。下图是对 random sensor network 做特征值分解后的特征向量分布展示，可以看到特征值越小，对应的特征向量越平滑。

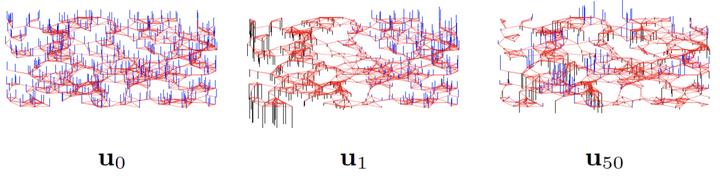
n阶对称矩阵一定有n个线性无关的特征向量。n维线性空间中的n个线性无关的向量都可以构成它的一组基。i.e. 下图中，当我们在这个空间中再画一个向量，这个向量都可以用下图中$u1$和$u2$来线性表示。

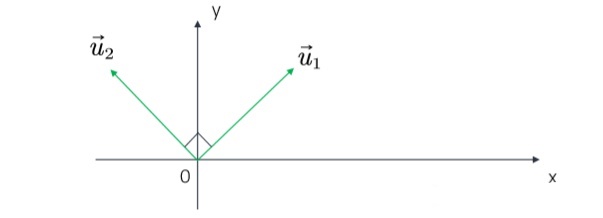
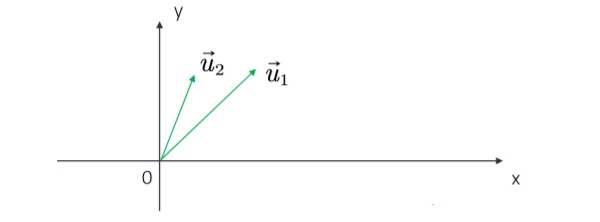
根据矩阵论的知识，对称矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。

➢ 拉普拉斯矩阵的n个特征向量是n维空间中的一组标准正交基。
$$\begin{gathered} U{U}^{\top }=I \\ L=U\Lambda U^{-1}=U\Lambda U^{\top } \end{gathered}$$

谱图卷积

首先来看图上的谱卷积。图上的谱卷积可以定义为信号 $x\in {\mathbb{R}}^N$ 与卷积核$g_{\theta }=\mathrm{diag}(\theta )$ ( $\theta \in {\mathbb{R}}^N)$ 在图上x和g卷积 $({}^{\ast }\mathrm{g}$ 看做一个符号也就是图上的卷积),

卷积是怎么操作的，请观看 5.5 卷积、卷积定理和傅里叶变换的关系及其性质

图上的卷积怎么做的，请观看7.2 图卷积算子，图卷积的演变过程，下面直接给出结论：

怎么办？首先分别左乘一个 $U^T$ ，然后左乘$U$逆变换回来，具体过程就是下面的形式：

我们把 $U^{T}g$ 用对角矩阵的形式写开就是上面第二个公式所表示的内容（他们所表示的含义都 是g进行傅里叶变换），在这里，可以将 $g_{\theta }$ 看作是 $L$ 特征向量的函数，也就是 $g_{\theta }(\Lambda )$ 。进一 步，我们可以推出下面的公式:

其中的函数 $g_{\theta }(\Lambda )$ 为卷积核的频率响应函数, $\theta$ 为待学习参数。以上就是频谱图卷积的一般 形式, 有许多频谱图卷积的工作以此式为核心展开。

直觉上来说，图卷积操作可以看成将原始的处于空域的图信号变换到频域上之后,对频域属性进行滤波，然后再恢复到原来的图信号所在的空域中，从而完成了对图信号的降噪与特征提取的功能，但以上不是该论文的要讨论的。

对于图谱卷积来说, 其计算代价无疑是很大的:

(1) 使用 $U$ 进行矩阵乘法运算的计算复杂 度为 $\mathcal{O}\left(N^2\right);$ (2) 计算大图的拉普拉斯矩阵 $L$ 的特征分解需要很大的计算量。

该论文的贡献是进行方法的改进和加速，这个非常的关键，论文写到：

• (i) they are not localized in space
• (ii) their learning complexity is in O(n)

因此提出采用一个多项式的滤波器来解决（也就是只考虑最近的邻居，远的邻居置为零）

进一步，作者提出了用切比雪夫多项式，因为切比雪夫多项式可以写成递归的形式，也就是之前计算过的中间结果后面就可以直接用，不必再进行计算。

该方法使用切比雪夫多项式 (Chebyshev polynomial) $T_k(x)$ 的 7.2 图卷积算子，图卷积的演变过程 意境级讲解

深入浅出图神经网络|GNN原理解析☄学习笔记图信号处理与图卷积神经网络

深入浅出图神经网络|GNN原理解析☄学习笔记图信号处理与图卷积神经网络

四 图卷积的公式推导

GCN：基于非局部图卷积神经网络的高光谱图像分类 | TGRS 2020

图卷积