5.10 Memory Networks 记忆网络的应用与方法
Posted 炫云云
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了5.10 Memory Networks 记忆网络的应用与方法相关的知识，希望对你有一定的参考价值。
文章目录
Memory Networks经典论文：
- Memory Networks (Facebook AI Research/2015)
- End-To-End Memory Networks(2015)
- Key-Value Memory Networks for Directly Reading Documents（2016）
- Ask Me Anything: Dynamic Memory Networks for Natural Language Processing (2016)
- Dynamic Memory Networks for Visual and Textual Question Answering (2016)
1、记忆网络
Memory Networks提出的最大卖点就是具备长期记忆（long-term memory），虽然当时RNN在文本处理领域十分有效，但是其对信息的长期记忆能力并不理想。Memory Networks的长期记忆思路其实也非常简单暴力，直接采用额外的记忆模块来保存之前的信息，而不是通过cell之间的hidden state传递。
框架
Memory Networks主要由一个记忆模块 m m m 和四个组件 I , G , O , R I, G, O, R I,G,O,R 构成
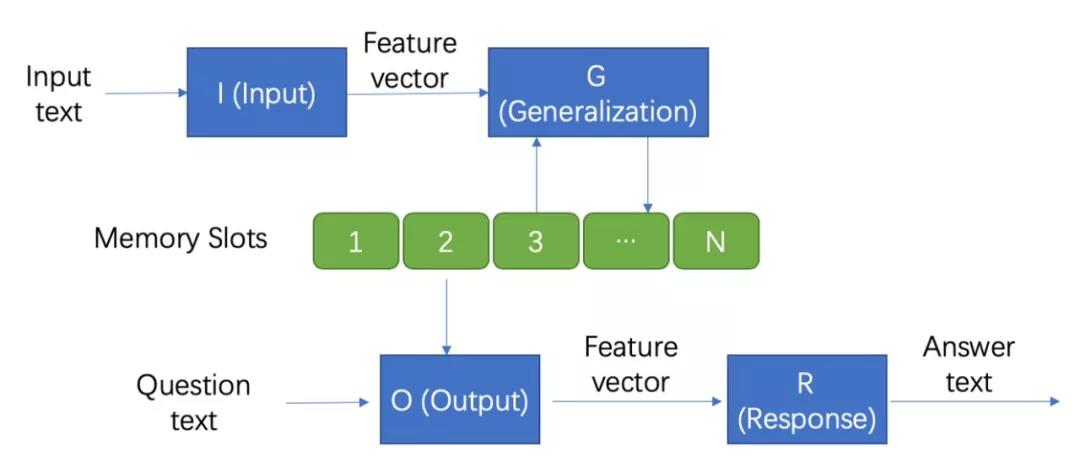
图 1 图1 图1
I: (input feature map)
用于将输入转化为网络里内在向量表示。（可以利用标准预处理，例如，文本输入的解析，共参考和实体解析。 还可以将输入编码为内部特征表示，例如，从文本转换为稀疏或密集特征向量）
G: (generalization)
用于更新记忆。简单的可以直接插入记忆数组中，复杂的可以将当前的记忆用于更新先前的记忆
O: (output feature map)
从记忆里结合输入，把合适的记忆抽取出来，返回一个向量。每次获得一个向量，代表了一次推理过程。
R: (response)
将上述向量转化回所需的格式，比如文字或者answer。
流程
考虑问答任务，Memory network的工作流程为：
-
给定一段输入x，通过组件I将x映射到向量空间
-
通过组件G更新记忆。论文中只是简单地将输入的向量插入到记忆槽中去。 m i = G ( m i , I ( x ) , m ) , ∀ i m_{i}=G\\left(m_{i}, I(x), m\\right), \\forall i mi=G(mi,I(x),m),∀i
-
利用组件O计算output feature。 o = O ( I ( x ) , m ) \\mathrm{o}=\\mathrm{O}(\\mathrm{I}(\\mathrm{x}), \\mathrm{m}) o=O(I(x),m)计算所求问题与记忆槽中的元素的相似度，可以返回一条或多条最相似的记忆
o 1 = O 1 ( x , m ) = arg max i = 1 , … , N s O ( x , m i ) o 2 = O 2 ( x , m ) = arg max i = 1 , … , N s O ( [ x , m o 1 ] , m i ) o_{1}=O_{1}(x, \\mathbf{m})=\\underset{i=1, \\ldots, N}{\\arg \\max } s_{O}\\left(x, \\mathbf{m}_{i}\\right)\\\\ o_{2}=O_{2}(x, \\mathbf{m})=\\underset{i=1, \\ldots, N}{\\arg \\max } s_{O}\\left(\\left[x, \\mathbf{m}_{o_{1}}\\right], \\mathbf{m}_{i}\\right) o1=O1(x,m)=i=1,…,NargmaxsO(x,mi)o2=O2(x,m)=i=1,…,NargmaxsO([x,mo1],mi)
-
对output feature进行解码，返回输出。
r = argmax w ∈ W s R ( [ q , o 1 , o 2 ] , w ) s R ( x , y ) = x U U T y r=\\operatorname{argmax}_{w \\in W} s_{R}\\left(\\left[q, o_{1}, o_{2}\\right], w\\right) \\\\s_{R}(x, y)=x U U^{T}y r=argmaxw∈WsR([q,o1,o2],w)sR(x,y)=xUUTy
损失函数
采用margin ranking loss，这个与支持向量机的损失函数类似。
∑
f
ˉ
≠
m
o
1
max
(
0
,
γ
−
s
O
(
x
,
m
o
1
)
+
s
O
(
x
,
f
ˉ
)
)
+
∑
f
ˉ
′
≠
m
02
max
(
0
,
γ
−
s
O
(
[
x
,
m
o
1
]
,
m
o
2
]
)
+
s
O
(
[
x
,
m
0
1
]
,
f
ˉ
′
]
)
)
+
∑
f
ˉ
′
≠
m
02
max
(
0
,
γ
−
s
O
(
[
x
,
m
o
1
]
,
m
o
2
]
)
+
s
O
(
[
x
,
m
0
1
]
,
f
ˉ
′
]
)
)
+
\\begin{array}{c} \\sum_{\\bar{f} \\neq \\mathbf{m}_{o_{1}}} \\max \\left(0, \\gamma-s_{O}\\left(x, \\mathbf{m}_{o 1}\\right)+s_{O}(x, \\bar{f})\\right)+ \\\\ \\left.\\left.\\sum_{\\bar{f}^{\\prime} \\neq \\mathbf{m}_{02}} \\max \\left(0, \\gamma-s_{O}\\left(\\left[x, \\mathbf{m}_{o_{1}}\\right], \\mathbf{m}_{o_{2}}\\right]\\right)+s_{O}\\left(\\left[x, \\mathbf{m}_{0_{1}}\\right], \\bar{f}^{\\prime}\\right]\\right)\\right)+ \\\\ \\left.\\left.\\sum_{\\bar{f}^{\\prime} \\neq \\mathbf{m}_{02}} \\max \\left(0, \\gamma-s_{O}\\left(\\left[x, \\mathbf{m}_{o_{1}}\\right], \\mathbf{m}_{o_{2}}\\right]\\right)+s_{O}\\left(\\left[x, \\mathbf{m}_{0_{1}}\\right], \\bar{f}^{\\prime}\\right]\\right)\\right)+ \\end{array}
∑fˉ=mo1max(0,γ−sO(x,mo1)+sO(x,fˉ))+∑fˉ′=m02max(0,γ−sO([x,mo1],mo2])+sO([x,m01],fˉ′]))+∑fˉ′论文解读：Dynamic Memory Networks for Visual and Textual Question Answering
论文阅读：End-To-End Memory Networks
论文阅读：End-To-End Memory Networks
论文阅读Ask me anything: Dynamic memory networks for natural language processing
文本分类Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification
文本分类Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification