5.12 CopyNet和 Pointer-Generator Net 复制机制和指针-生成器网络
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了5.12 CopyNet和 Pointer-Generator Net 复制机制和指针-生成器网络相关的知识,希望对你有一定的参考价值。
Seq2Seq的复制机制即输入序列中的某些片段被选择性地复制到输出序列中。
从认知的角度来看,复制机制与死记硬背有关,需要较少的理解,但确保了高度的文字忠实度。从建模的角度来看,复制操作更加刚性和象征性,这使得它比软注意机制更难集成到一个完全可微分的神经模型中。
COPYNET1是一个具有复制机制的可微分Seq2Seq模型,它可以通过梯度下降以端到端方式进行训练。
Pointer-Generator Networ 2(指针-生成器网络)与COPYNET类似。它可以通过指向从源文本复制单词,这有助于准确地复制信息,同时保留通过生成器产生新单词的能力。其次, 使用覆盖来跟踪已经生成的内容,这就不鼓励重复。
CopyNet
如图1所示,CopyNet仍然是一个编码器-解码器。Encoder将源序列转换为表征,然后由Decoder读取表征以生成目标序列。
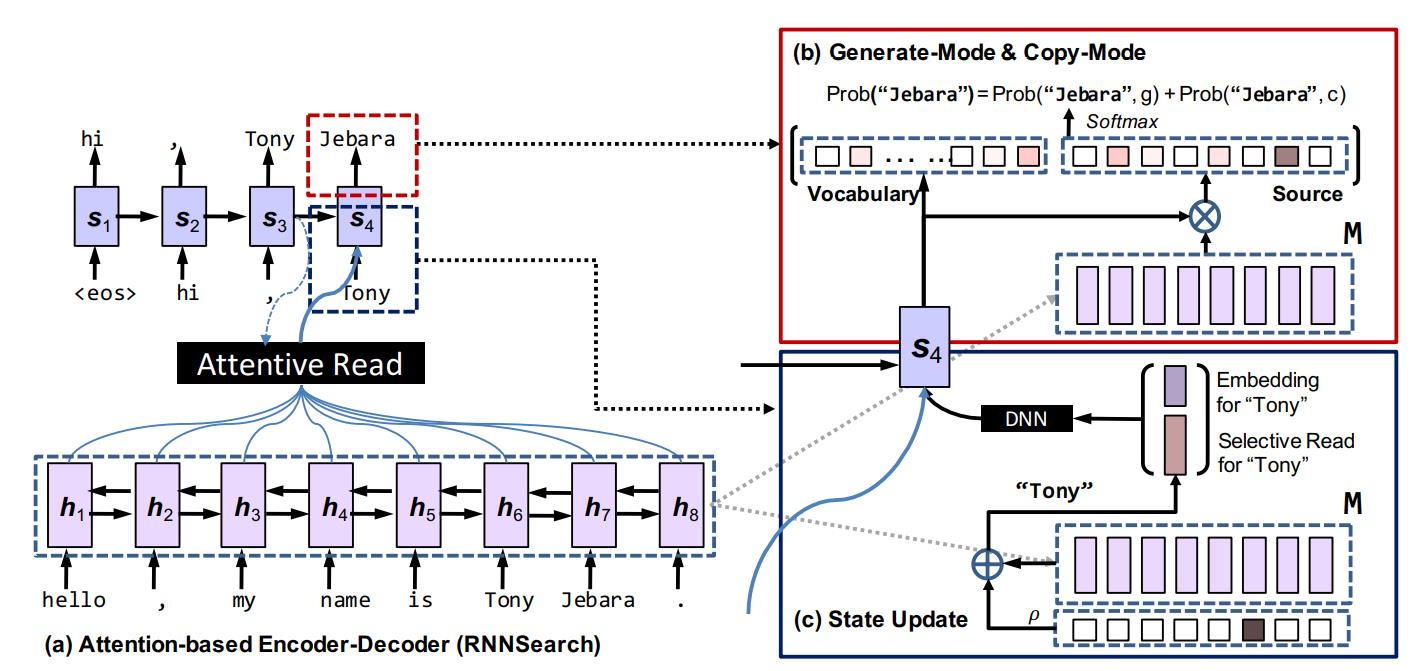
图
1
图1
图1
Encoder: 一个biRNN将源序列转换为隐藏状态,每个隐藏状态
h
t
\\mathbf{h}_{t}
ht 对应一个单词
x
t
x_{t}
xt。这种新的源表征
{
h
1
,
…
,
h
T
S
}
\\left\\{\\mathbf{h}_{1}, \\ldots, \\mathbf{h}_{T_{S}}\\right\\}
{h1,…,hTS}被认为是一种短期记忆,记作
M
\\mathbf{M}
M,之后将以多种方式访问它,以生成目标序列(解码)。
Decoder: RNN读取 M \\mathbf{M} M并生成目标序列。它与标椎rnn解码器相似,但是有以下重要的区别
- 预测: COPYNET基于两种模式的混合概率模型预测单词,即生成模式和复制模式,后者从源序列中选择单词
- 状态的更新: 在 t − 1 t-1 t−1时刻预测的单词被用于更新 t t t的状态,但是COPYNET不仅使用它的单词嵌入,而且还使用它在 M \\mathbf{M} M(如果有的话)中对应的特定位置的隐藏状态。
- 读取 M \\mathbf{M} M : 除了对 M M M的 注意力读之外,COPYNET还对 M \\mathbf{M} M有“选择性读”,这导致了基于内容的寻址和基于位置的寻址的强大混合
1、预测的复制和生成
假设一个词汇表 V = { v 1 , … , v N } \\mathcal{V}=\\left\\{v_{1}, \\ldots, v_{N}\\right\\} V={v1,…,vN},并且对任何超出词汇表(OOV)的单词使用UNK。
此外,我们还有另一组单词 X \\mathcal{X} X, 为源序列 X = X= X= { x 1 , … , x T S } \\left\\{x_{1}, \\ldots, x_{T_{S}}\\right\\} {x1,…,xTS}中所有唯一的单词。因为 X \\mathcal{X} X可能包含不在 V \\mathcal{V} V中的单词,所以复制 X X X中的子序列可以使COPYNET输出一些OOV单词。简而言之, 源序列 X X X的实例特定词汇表是 V ∪ U N K ∪ X \\mathcal{V} \\cup \\mathrm{UNK} \\cup \\mathcal{X} V∪UNK∪X。
给定解码器RNN状态
s
t
\\mathbf{s}_{t}
st在
t
t
t时刻和
M
\\mathbf{M}
M,生成任何目标词
y
t
y_{t}
yt的概率由以下概率的“混合”给出 以上是关于5.12 CopyNet和 Pointer-Generator Net 复制机制和指针-生成器网络的主要内容,如果未能解决你的问题,请参考以下文章
p
(
y
t
∣
s
t
,
y
t
−
1
,
c
t
,
M
)
=
p
(
y
t
,
g
∣
s
t
,
y
t
−
1
,
c
t
,
M
)
+
p
(
y
t
,
c
∣
s
t
,
y
t
−
1
,
c
t
,
M
)
(1)
\\begin{aligned} p\\left(y_{t} \\mid \\mathbf{s}_{t}, y_{t-1}, \\mathbf{c}_{t}, \\mathbf{M}\\right) &=p\\left(y_{t}, \\mathrm{~g} \\mid \\mathbf{s}_{t}, y_{t-1}, \\mathbf{c}_{t}, \\mathbf{M}\\right) +p\\left(y_{t}, \\mathbf{c} \\mid \\mathbf{s}_{t}, y_{t-1}, \\mathbf{c}_{t}, \\mathbf{M}\\right) \\end{aligned}\\tag{1}
p(yt∣st,yt−1,ct,M)=p(yt, g∣st,yt−1,ct,M)+p(yt,c∣st,yt−1,ct,M)(1)
其中
g
\\mathrm{g}
g 为生成模式和
c
\\mathrm{c}
c为复制模式。两模态发生的概率分别为
p
(
y
t
,
g
∣
⋅
)
=
{
1
Z
e
ψ
g
(
y
t
)
,
y
t
∈
V
0
,
y
t
∈
X
∩
V
ˉ
1
Z
e
ψ
g
(
U
N
K
)
y
t
∉
V
∪
X
(2)
\\begin{array}{l} p\\left(y_{t}, \\mathrm{~g} \\mid \\cdot\\right)=\\left\\{\\begin{array}{cc} \\frac{1}{Z} e^{\\psi_{g}\\left(y_{t}\\right)}, & y_{t} \\in \\mathcal{V} \\\\ 0, & y_{t} \\in \\mathcal{X} \\cap \\bar{V} \\\\ \\frac{1}{Z} e^{\\psi_{g}(\\mathrm{UNK})} & y_{t} \\notin \\mathcal{V} \\cup \\mathcal{X} \\end{array}\\right. \\\\ \\end{array}\\tag{2}
p(yt, g∣⋅)=⎩⎨⎧Z1eψg(yt),0,Z1eψg(UNK)yt∈Vyt∈X∩Vˉyt∈/V∪X(2)
p
(
y
t
,
c
∣
⋅
)
=
{
1
Z
∑
j
:
x
j
=
y
t
e
ψ
c
(
x