向量的叉积向量积
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了向量的叉积向量积相关的知识,希望对你有一定的参考价值。
引例:力作用在杠杆上的力矩
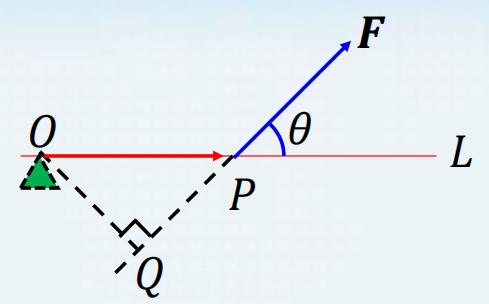
设
O
O
O 为 杜杆
L
L
L 的支点, 力
F
\\boldsymbol{F}
F 作用于 这杠杆的点
P
P
P 处,
F
\\boldsymbol{F}
F 与
O
P
→
\\overrightarrow{O P}
OP 的夹角 为
θ
\\theta
θ ,那么,力
F
\\boldsymbol{F}
F 对支点
O
O
O的力矩
M
M
M 是一个向量,它的模为
∣
M
∣
=
∣
O
Q
∣
∣
F
∣
=
∣
O
P
→
∣
∣
F
∣
sin
θ
|M|=|O Q||\\boldsymbol{F}|=|\\overrightarrow{O P}||\\boldsymbol{F}| \\sin \\theta
∣M∣=∣OQ∣∣F∣=∣OP∣∣F∣sinθ
它的方向垂直于
O
P
→
\\overrightarrow{O P}
OP 与
F
\\boldsymbol{F}
F 所决定的平面, 并且按右手法则从
O
P
→
\\overrightarrow{O P}
OP 以不超过
π
\\pi
π 的角
θ
\\theta
θ 转向
F
F
F确定.这里力矩
M
M
M方向垂直朝外
问题:向量的向量积
向量积的定义与性质
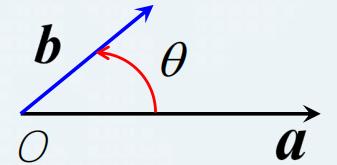
定
义
1
\\large\\color{magenta}{\\boxed{\\color{brown}{定义1} }}
定义1 向量
a
a
a 与
b
b
b 的向量积 (或叉积) 是一个向量,记作
a
×
b
\\boldsymbol{a} \\times \\boldsymbol{b}
a×b,它的长度规定为
∣
a
×
b
∣
=
∣
a
∣
∣
b
∣
sin
⟨
a
,
b
⟩
,
|\\boldsymbol{a} \\times \\boldsymbol{b}|=|\\boldsymbol{a}||\\boldsymbol{b}| \\sin \\langle\\boldsymbol{a}, \\boldsymbol{b}\\rangle,
∣a×b∣=∣a∣∣b∣sin⟨a,b⟩,
它的方向规定为:与
a
,
b
\\boldsymbol{a}, \\boldsymbol{b}
a,b 都垂直,并且使
a
,
b
,
a
×
b
\\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{a} \\times \\boldsymbol{b}
a,b,a×b 构成右手系, 即当右手四指从
a
a
a 以不超过
π
\\pi
π 的角
θ
\\theta
θ 弯向
b
b
b 时,拇指的指向 .
【注1】 a × b = 0 \\quad a \\times b=0 a×b=0 的充分必要条件是 a , b \\boldsymbol{a}, \\boldsymbol{b} a,b 共线
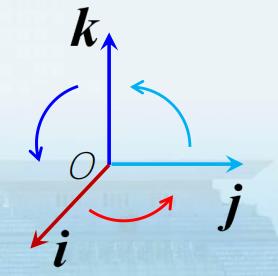
【注2】 i × j = k , j × k = i , k × i = j \\quad \\boldsymbol{i} \\times \\boldsymbol{j}=\\boldsymbol{k}, \\boldsymbol{j} \\times \\boldsymbol{k}=\\boldsymbol{i}, \\boldsymbol{k} \\times \\boldsymbol{i}=\\boldsymbol{j} i×j=k,j×k=i,k×i=j,
在二维空间内, 向量
a
=
(
a
1
,
a
2
)
,
b
=
(
b
1
,
b
2
)
a= (\\mathrm{a}_{1}, \\mathrm{a}_{2} ), \\mathrm{b}= (\\mathrm{b}_{1}, \\mathrm{~b}_{2})
a=(a1,a2),b=(b1, b2)
a
×
b
=
∣
a
1
a
2
b
1
b
2
∣
=
a
1
b
2
−
a
2
b
1
\\boldsymbol{a} \\times \\boldsymbol{b}=\\left|\\begin{array}{ll} a_{1} & a_{2} \\\\ b_{1} & b_{2} \\end{array}\\right|=a_{1} b_{2}-a_{2} b_{1}
a×b=∣∣∣∣a1b1a2b2∣∣∣∣=a1b2−a2b1
向量积的几何意义
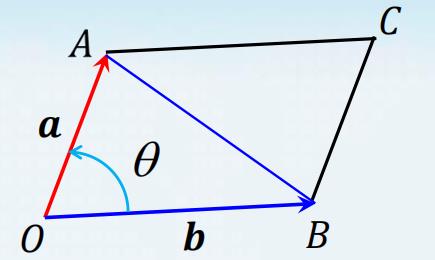
∣ a × b ∣ |a \\times b| ∣a×b∣ 为以 a a a 和 b b b 为邻边的平行四边形的面积.
【注 】 三角形 O A B O A B OAB 的面积为 1 2 ∣ a × b ∣ \\frac{1}{2}|\\boldsymbol{a} \\times \\boldsymbol{b}| 21∣a×b∣
两个相同向量的叉积是0,
A
×
A
=
0
A \\times A=0
A×A=0
如果用几何意义解释,二者构成一条线段,线段的面积是0。
在方向上,叉积垂直于平行四边形所在的平面:
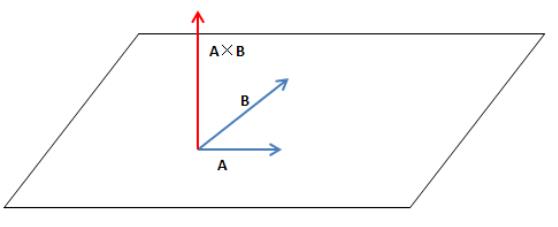
向量积的性质
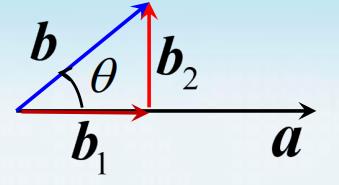
命 题 1 \\large\\color{magenta}{\\boxed{\\color{brown}{命题1} }} 命题1 设 a ≠ 0 \\boldsymbol{a} \\neq \\mathbf{0} a=0, 则 a × b = a × b 2 . \\boldsymbol{a} \\times \\boldsymbol{b}=\\boldsymbol{a} \\times \\boldsymbol{b}_{\\mathbf{2}} . a×b=a×b2.其中 b 2 \\boldsymbol{b}_{2} b2 是 b \\boldsymbol{b} b 关于 a a a 的外投影向量
例如,设 b b b 关于 a a a 的正交分解为 b = b 1 + b 2 b=b_{1}+b_{2} b=b1+b2,其中 b 1 , b 2 \\boldsymbol{b}_{1}, \\boldsymbol{b}_{2} b1,b2 分别是 b \\boldsymbol{b}