向量的混合积
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了向量的混合积相关的知识,希望对你有一定的参考价值。
向量之间的位置关系
垂直 ⇔ a ⋅ b = 0 \\Leftrightarrow \\boldsymbol{a} \\cdot \\boldsymbol{b}=0 \\quad ⇔a⋅b=0
平行 ⇔ a × b = 0 \\Leftrightarrow \\boldsymbol{a} \\times \\boldsymbol{b}=\\mathbf{0} \\quad ⇔a×b=0
共面 ⇔ \\Leftrightarrow ⇔ a , b , c \\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{c} a,b,c 线性相关
投影、面积与体积的计算
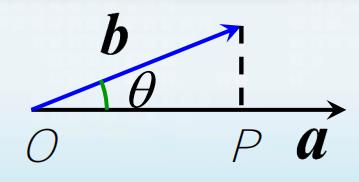
Π
a
(
b
)
=
b
⋅
a
∘
\\Pi_{\\boldsymbol{a}}(\\boldsymbol{b})=\\boldsymbol{b} \\cdot \\boldsymbol{a}^{\\circ}
Πa(b)=b⋅a∘

平行四边形的面积
S
=
∣
a
×
b
∣
\\begin{array}{c} \\text { 平行四边形的面积 } \\\\ S=|\\boldsymbol{a} \\times \\boldsymbol{b}| \\end{array}
平行四边形的面积 S=∣a×b∣
问题:如何求平行六面体的体积?
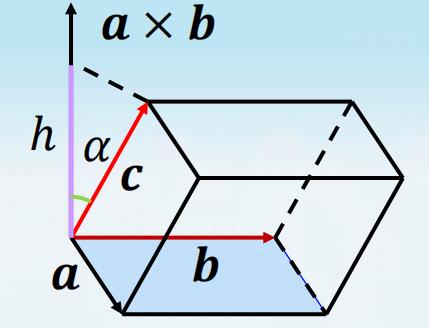
以 a , b , c a, b, c a,b,c 为棱作平行六面体, 则底面积: A = ∣ a × b ∣ A=|\\boldsymbol{a} \\times \\boldsymbol{b}| A=∣a×b∣ ,高: h = ∣ c ∣ ∣ cos α ∣ h=|\\boldsymbol{c}||\\cos \\alpha| h=∣c∣∣cosα∣
故平行六面体体积为
V
六面体
=
A
h
=
∣
a
×
b
∣
∣
c
∥
cos
α
∣
=
∣
(
a
×
b
)
⋅
c
∣
\\begin{aligned} V_{\\text {六面体 }} &=A h=|\\boldsymbol{a} \\times \\boldsymbol{b}| \\mid \\boldsymbol{c} \\| \\cos \\alpha \\mid \\\\ &=|(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot \\boldsymbol{c}| \\end{aligned}
V六面体 =Ah=∣a×b∣∣c∥cosα∣=∣(a×b)⋅c∣
(
注
)
\\Large\\color{violet}{(注) }
(注) 当
a
,
b
,
c
\\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{c}
a,b,c 为右手系时,
cos
α
>
0
\\quad \\cos \\alpha>0
cosα>0, 则
(
a
×
b
)
⋅
c
>
0
(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot \\boldsymbol{c} >0
(a×b)⋅c>0 .
混合积的定义与性质
定
义
1
\\large\\color{magenta}{\\boxed{\\color{brown}{定义1} }}
定义1
\\quad
向量
a
,
b
,
c
\\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{c}
a,b,c 的混合积(记作
(
a
b
c
)
(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})
(abc) ) 是一个数量:
(
a
b
c
)
=
(
a
×
b
)
⋅
c
(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})=(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot \\boldsymbol{c}
(abc)=(a×b)⋅c
混合积的几何意义
V
平行六面体
=
∣
(
a
b
c
)
∣
.
V_{\\text {平行六面体 }}=|(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})| .
V平行六面体 =∣(abc)∣.
(
注
1
)
\\Large\\color{violet}{(注1) }
(注1)
∣
(
a
b
c
)
∣
≤
∣
a
∣
∣
b
∣
∣
c
∣
|(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})| \\leq|\\boldsymbol{a}||\\boldsymbol{b}||\\boldsymbol{c}|
∣(abc)∣≤∣a∣∣b∣∣c∣.
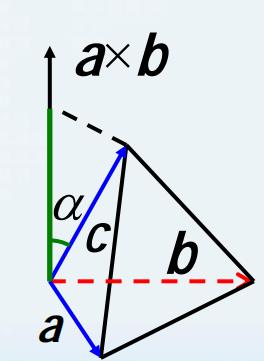
( 注 2 ) \\Large\\color{violet}{(注2) } (注2) 以 a , b , c a, b, c a,b,c 为棱的四面体的体积
V
四面体
=
1
6
∣
(
a
b
c
)
∣
=
1
6
∣
(
a
×
b
)
⋅
c
∣
V_{\\text {四面体 }}=\\frac{1}{6}|(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})|=\\frac{1}{6}|(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot \\boldsymbol{c}|
V四面体 =61∣(abc)∣=61∣(a×b)⋅c∣
性质
(1) 轮换对称性 ( a b c ) = ( b c a ) = ( c a b ) . \\quad(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})=(\\boldsymbol{b} \\boldsymbol{c} \\boldsymbol{a})=(\\boldsymbol{c} \\boldsymbol{a} \\boldsymbol{b}) . (abc)=(bca)=(cab).
(2) 反交换律 ( a b c ) = − ( b a c ) = − ( c b a ) . \\quad(\\boldsymbol{a} \\boldsymbol{b} \\boldsymbol{c})=-(\\boldsymbol{b} \\boldsymbol{a} \\boldsymbol{c})=-(\\boldsymbol{c} \\boldsymbol{b} \\boldsymbol{a}) . (abc)=−(bac)=−(cba).
(3) ( a × b ) ⋅ c = a ⋅ ( b × c ) (\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot \\boldsymbol{c}=\\boldsymbol{a} \\cdot(\\boldsymbol{b} \\times \\boldsymbol{c}) (a×b)⋅c=a⋅(b×c)
(4) 当 a , b , c \\boldsymbol{a}, \\boldsymbol{b}, \\boldsymbol{c} a,b,c 中有两个向量相同时,它们的混合积为 0. 0 . 0.
例
1
\\Large\\color{violet}{例1}
例1 证明拉格朗日恒等式:
(
a
×
b
)
⋅
(
c
×
d
)
=
∣
a
⋅
c
a
⋅
d
b
⋅
c
b
⋅
d
∣
.
\\quad(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot(\\boldsymbol{c} \\times \\boldsymbol{d})=\\left|\\begin{array}{ll}\\boldsymbol{a} \\cdot \\boldsymbol{c} & \\boldsymbol{a} \\cdot \\boldsymbol{d} \\\\ \\boldsymbol{b} \\cdot \\boldsymbol{c} & \\boldsymbol{b} \\cdot \\boldsymbol{d}\\end{array}\\right| .
(a×b)⋅(c×d)=∣∣∣∣a⋅cb⋅ca⋅db⋅d∣∣∣∣.
【证】 记
h
=
c
×
d
\\boldsymbol{h}=\\boldsymbol{c} \\times \\boldsymbol{d}
h=c×d, 则
(
a
×
b
)
⋅
(
c
×
d
)
=
(
a
×
b
)
⋅
h
=
a
⋅
(
b
×
h
)
(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot(\\boldsymbol{c} \\times \\boldsymbol{d})=(\\boldsymbol{a} \\times \\boldsymbol{b}) \\cdot \\boldsymbol{h}=\\boldsymbol{a} \\cdot(\\boldsymbol{b} \\times \\boldsymbol{h})
(a×b)⋅(c×d)=