线性映射06——线性变换
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性映射06——线性变换相关的知识,希望对你有一定的参考价值。
- 线性映射01——映射的概念和性质
- 线性映射02—— 线性映射概念与运算
- 线性映射03——线性空间的同构
- 线性映射04——像与核
- 线性映射05——代数与代数同构
- 线性映射06——线性变换
- 线性映射07——线性变换的矩阵表示
- 线性映射08——不变子空间
- 线性映射9——对偶空间
线性变换
定 义 1 \\large\\color{magenta}{\\boxed{\\color{brown}{定义1 } }} 定义1 线性空间 V \\boldsymbol{V} V ,数域 F , T \\boldsymbol{F}, \\boldsymbol{T} F,T 是 V \\boldsymbol{V} V 中的变换. 若对 ∀ x , y ∈ V , ∀ k , l ∈ K \\forall \\boldsymbol{x}, \\boldsymbol{y} \\in \\boldsymbol{V}, \\forall \\boldsymbol{k}, \\boldsymbol{l} \\in \\boldsymbol{K} ∀x,y∈V,∀k,l∈K ,有加法不变性和数乘不变性,即
都有 T ( k x + l y ) = k ( T x ) + l ( T y ) , \\boldsymbol{T}(\\boldsymbol{k} \\boldsymbol{x}+\\boldsymbol{l} \\boldsymbol{y})=\\boldsymbol{k}(\\boldsymbol{T} \\boldsymbol{x})+\\boldsymbol{l}(\\boldsymbol{T} \\boldsymbol{y}), \\quad T(kx+ly)=k(Tx)+l(Ty), 称 T \\boldsymbol{T} T 是 V \\boldsymbol{V} V 中的线性变换.
线性变换:同一个 F \\boldsymbol{F} F - 空间上的线性映射 A : V → V \\mathcal{A}: \\boldsymbol{V} \\rightarrow \\boldsymbol{V} A:V→V
注 : \\Large{\\color{violet}{注:}} 注: 线性变换是同构映射吗?二者有什么区别?前者是后者的特殊情况?还是 后者是前者的特殊情况?
几何变换:
(1) 坐标面上的投影: A x y : R 3 → R 3 , ( x , y , z ) ↦ ( x , y , 0 ) \\mathcal{A}_{x y}: \\mathbb{R}^{3} \\rightarrow \\mathbb{R}^{3},(x, y, z) \\mapsto(x, y, 0) Axy:R3→R3,(x,y,z)↦(x,y,0)
(2) 坐标轴上的投影: A z : ( x , y , z ) ↦ ( 0 , 0 , z ) \\mathcal{A}_{z}:(x, y, z) \\mapsto(\\mathbf{0}, \\mathbf{0}, z) Az:(x,y,z)↦(0,0,z)
(3) 关于坐标面的镜面反射: B x y : ( x , y , z ) ↦ ( x , y , − z ) \\mathcal{B}_{x y}:(x, y, z) \\mapsto(x, y,-z) Bxy:(x,y,z)↦(x,y,−z)
(4) 绕 z 轴旋转: C θ : ( x , y , z ) ↦ ( x , y , z ) ( cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ) \\begin{array}{ll}\\text { 绕 } z \\text { 轴旋转: } & \\mathcal{C}_{\\theta}:(\\boldsymbol{x}, \\boldsymbol{y}, z) \\mapsto(\\boldsymbol{x}, \\boldsymbol{y}, \\boldsymbol{z})\\left(\\begin{array}{ccc}\\cos \\theta & -\\sin \\theta & 0 \\\\ \\sin \\theta & \\cos \\theta & 0 \\\\ \\mathbf{0} & \\mathbf{0} & \\mathbf{1}\\end{array}\\right)\\end{array} 绕 z 轴旋转: Cθ:(x,y,z)↦(x,y,z)⎝⎛cosθsinθ0−sinθcosθ0001⎠⎞
线性变换举例
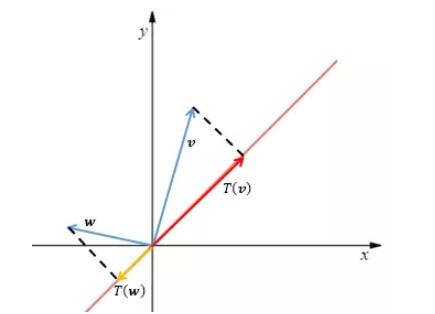
投影变换:通过 T T T变换,使平面内的一个向量投影到一条直线上。
T T T就像一个函数:给定一个输入向量,经过 T T T的变换,输出成直线上的投影,下图中 v v v和 w w w是 R 2 R^{2} R2 空 间 内 的 向 量 , 通 过 T 变 换 变 成 了 直 线 上 的投影, 即 T ( v ) T(v) T(v)和 T ( w ) T( \\mathbf{w}) T(w) :
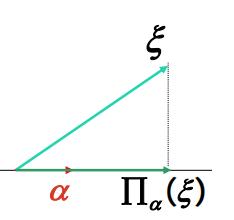
投影变换是线性变换:
设
V
=
R
3
V=R^{3}
V=R3, 变换
Π
α
\\Pi_{\\alpha}
Πα 为向量在
α
\\alpha
α 上的内射影, 即:
Π
α
:
R
3
→
R
3
,
ξ
↦
(
α
,
ξ
)
(
α
,
α
)
α
,
∀
ξ
∈
R
3
\\Pi_{\\alpha}: R^{3} \\rightarrow R^{3}, \\xi \\mapsto \\frac{(\\alpha, \\xi)}{(\\alpha, \\alpha)} \\alpha, \\forall \\xi \\in R^{3}
Πα:R3→R3,ξ↦(α,α)(α,ξ)α,∀ξ∈R3
易验证:
∀
ξ
,
η
∈
R
3
,
∀
k
∈
R
\\forall \\xi, \\eta \\in R^{3}, \\forall k \\in R
∀ξ,η∈R3,∀k∈R
Π
α
(
ξ
+
η
)
=
Π
α
(
ξ
)
+
Π
α
(
η
)
Π
α
(
k
ξ
)
=
k
∏
α
(
ξ
)
\\Pi_{\\alpha}(\\xi+\\eta)=\\Pi_{\\alpha}(\\xi)+\\Pi_{\\alpha}(\\eta)\\\\ \\Pi_{\\alpha}(k \\xi)=k \\prod_{\\alpha}(\\xi)
Πα(ξ+η)=Πα(ξ)+Πα(η)Πα(kξ)=kα∏(ξ)
V
=
P
[
x
]
\\boldsymbol{V}=P[x]
V=P[x] 或
P
[
x
]
n
P[x]_{n}
P[x]n 上的求微商是一个 线性变换,用
D
D
D表示,即
D
:
V
→
V
,
D
(
f
(
x
)
)
=
f
′
(
x
)
,
∀
f
(
x
)
∈
V
D: V \\rightarrow V, \\quad D(f(x))=f^{\\prime}(x), \\forall f(x) \\in V
D:V→V,D(f(x))=f′(x),∀以上是关于线性映射06——线性变换的主要内容,如果未能解决你的问题,请参考以下文章