空间直线及其方程
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了空间直线及其方程相关的知识,希望对你有一定的参考价值。
直线是随处可见的空间形状

问题:如何从几何上确定一个空间直线?
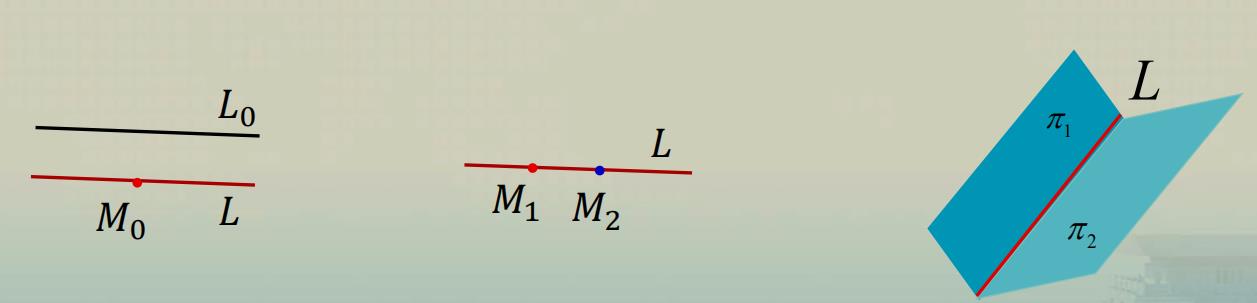
- 过一定点可以作唯一直线平行于一定直线.
- 两点可以确定一条直线.
- 任意一条直线可以视为两相交平面的交线.
空间直线的参数方程
过一定点可以作唯一直线平行于一定直线.
任何平行于直线的非零向量 v v v 称为直线的方向向量.
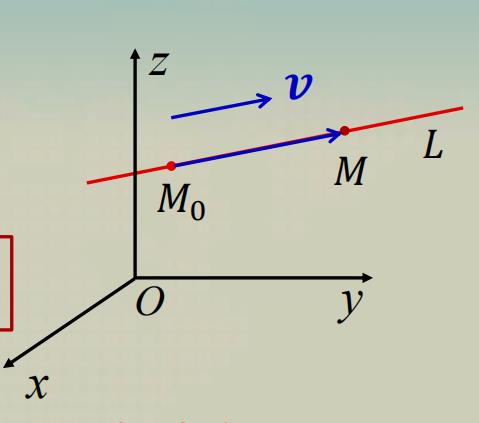
要素:点 M 0 ( x 0 , y 0 , z 0 ) , M_{0}\\left(x_{0}, y_{0}, z_{0}\\right), M0(x0,y0,z0), 方向向量 v = ( m , n , p ) v=(m, n, p) v=(m,n,p).
与 v v v 平行的所有非零向量均可作为此直线的方向向量. 直线上的所有向量都与该直线的方向向量平行.
任务:求直线 𝐿 𝐿 L 的方程即动点 𝑀 ( 𝑥 , 𝑦 , 𝑧 ) 𝑀(𝑥, 𝑦, 𝑧) M(x,y,z)的轨迹方程.
依据: M 0 M → \\overrightarrow{M_{0} M} M0M 与方向向量 v v v 平行 .
关系: M 0 M → = t v \\large{\\color{red}{\\overrightarrow{M_{0} M}=t \\boldsymbol{v}}} M0M=tv
要 素 \\Large\\color{violet}{要素} 要素 点 M 0 ( x 0 , y 0 , z 0 ) , M_{0}\\left(x_{0}, y_{0}, z_{0}\\right), M0(x0,y0,z0), 方向向量 v = ( m , n , p ) v=(m, n, p) v=(m,n,p).
关系:
M
0
M
→
=
t
v
\\large{\\color{red}{\\overrightarrow{M_{0} M}=t \\boldsymbol{v}}}
M0M=tv ,得到
直
线
𝑳
的
参
数
方
程
\\large\\color{#70f3ff}{\\boxed{\\color{green}{直线 𝑳 的参数方程}}}
直线L的参数方程
L
:
{
x
=
x
0
+
m
t
y
=
y
0
+
n
t
,
−
∞
<
t
<
+
∞
.
z
=
z
0
+
p
t
L:\\left\\{\\begin{array}{l}x=x_{0}+m t \\\\ y=y_{0}+n t,\\quad-\\infty<t<+\\infty . \\quad \\\\ z=z_{0}+p t\\end{array}\\right.
L:⎩⎨⎧x=x0+mty=y0+nt,−∞<t<+∞.z=z0+pt
【注1】 直线方程只含一个自由参数,通常说直线是一维的 .
【注2】 直线可以看作匀速运动的质点的轨迹,其中 𝒗 是速度,𝑡是时间.
空间直线的向量式方程
关系: M 0 M → = t v \\large{\\color{red}{\\overrightarrow{M_{0} M}=t \\boldsymbol{v}}} M0M=tv
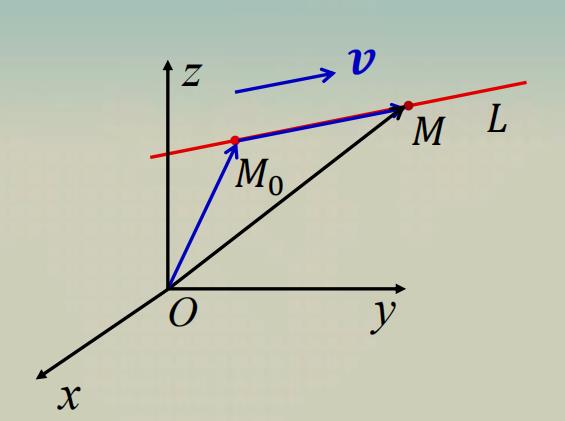
由 r = O M → = ( x , y , z ) r=\\overrightarrow{O M}=(x, y, z) r=OM=(x,y,z) , r 0 = O M 0 → = ( x 0 , y 0 , z 0 ) r_0=\\overrightarrow{O M_0}=(x_0, y_0, z_0) r0=OM0=(x0,y0,z0) 可以得到
L = r 0 + t v ⟶ {L} =r_{0}+t v\\longrightarrow L=r0+tv⟶ 直 线 𝑳 的 向 量 式 方 程 \\large\\color{#70f3ff}{\\boxed{\\color{green}{直线 𝑳 的向量式方程}}} 直线L的向量式方程
直线的点向式方程
要素:点 M 0 ( x 0 , y 0 , z 0 ) , M_{0}\\left(x_{0}, y_{0}, z_{0}\\right), M0(x0,y0,z0), 方向向量 v = ( m , n , p ) v=(m, n, p) v=(m,n,p).
依据: M 0 M → \\overrightarrow{M_{0} M} M0M 与方向向量 v v v 平行 . . .
关系:
M
0
M
→
×
v
=
0
或
M
0
M
→
=
t
v
\\large{\\color{red}{ \\overrightarrow{M_{0} M} \\times \\boldsymbol{v}=\\mathbf{0} \\text { 或 } \\overrightarrow{M_{0} M}=t \\boldsymbol{v}}}
M0M×v=0 或