剑指offer_二维数组中的查找

Posted 2021-06-07 红颜莫知己

题目描述

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7，返回 true。

给定 target = 3，返回 false。

示例1
输入：7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值：true
说明存在7，返回true

示例2
输入：3,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值：false
说明不存在3，返回false

方法一：二维数组的二分查找

• 由于数组是有序的，对二维数组的每一行进行二分查找即可

java代码：

public class Solution {
    public boolean Find(int target, int [][] array) {
        for (int i = 0 ; i < array.length ; i++) {
        	//定义左指针
            int left = 0;
            //定义右指针
            int right = array[i].length - 1;
            while(left <= right) {
                int mid = (right + left) / 2;
                if (array[i][mid] < target) {
                    left = mid + 1;
                }else if(array[i][mid] > target) {
                    right = mid - 1;
                }else {
                    return true;
                }
            }
        }
        return false;
    }     
}

复杂度分析

时间复杂度

O(mlogn):数组的列长度为m，每行二分查找需要logn

空间复杂度

O(1)

方法二

由于这个数组是有序的，我们可以从左下角或右上角进行检查

• 若目标值小于右上角值，则说明目标值只可能在右上角值所在列的左边，重新定义右上角值
  
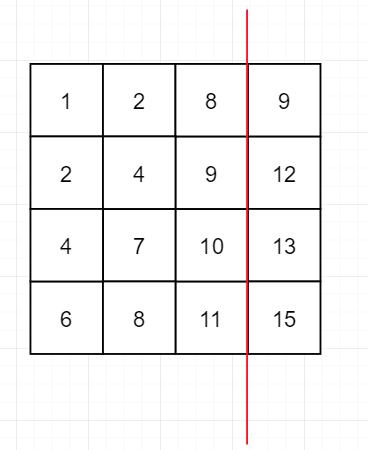
  若目标值大于新的右上角值，则目标值一定在右上角值所在行的下面
  
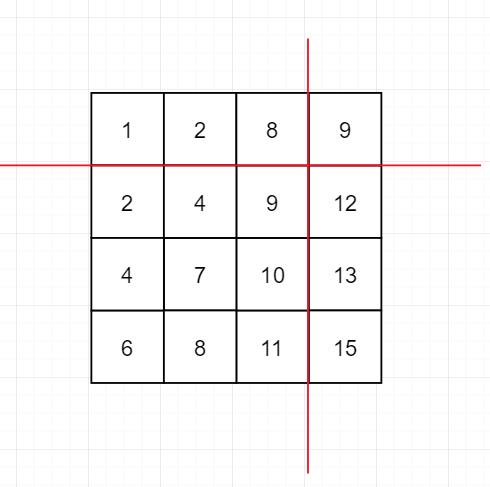
• 一直这样下去，若存在目标值，就一定能找到

java代码：

public class Solution {
    public boolean Find(int target, int [][] array) {
        int row = 0;
        int col = array[0].length - 1;
        while (row <= array.length - 1 && col >= 0) {
            if (target == array[row][col]) {
                return true;
            }else if (target > array[row][col]) {
                row++;
            }else {
                col--;
            }
        }
        return false;
    }    
}

复杂度分析

时间复杂度

O(m+n)：m行n列，这是最坏情况下，只有当m比n小的多的时候，第一种才比第二种好

空间复杂度

O(1)

若有误，请指教！！！