VLSI数字信号处理系统——第十章流水线结构的并行自适应递归滤波器
Posted 夏风喃喃
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了VLSI数字信号处理系统——第十章流水线结构的并行自适应递归滤波器相关的知识,希望对你有一定的参考价值。
VLSI数字信号处理系统——第十章流水线结构的并行自适应递归滤波器
作者:夏风喃喃
参考:
(1) VLSI数字信号处理系统:设计与实现 (美)Keshab K.Parhi/著
(2) socvista https://wenku.baidu.com/u/socvista?from=wenku
文章目录
一. 引言
经典的滤波器分两类:FIR和IIR。FIR是有限长冲击响应滤波器,硬件电路是非递归的;而IIR是无限长冲击响应滤波器,硬件电路存在递归环路,值得注意的是,IIR可以看成是一个FIR和递归环路的级联。
非递归运算通常采用流水线或者并行处理架构,而自适应递归滤波器由于本身的反馈回路,无法简单的套用这类架构。本章重点在如何采用超前计算(look-ahead computation)、增量块处理(incremental block processing)技术、基于最小均方误差(Least-Mean-Square,LMS)流水计算的弛豫超前(relaxed look-ahead)变换以及格型自适应滤波的方法,在自适应递归数字滤波器中实现流水线和并行处理。
二. 数字滤波器中的流水线交织操作
本节以一阶递归数字滤波器为例,回顾流水线交织操作的概念。
对于数字滤波器的流水线结构本节提供M倍降速设计方法,下节提供超前计算设计方法。将M倍降速和超前计算结合起来将更加高效,先用超前计算构造“自交织”的流水IIR节,然后再用M倍降速构造“独立交织”的IIR节。
2.1 低效率的单通道/多通道交织
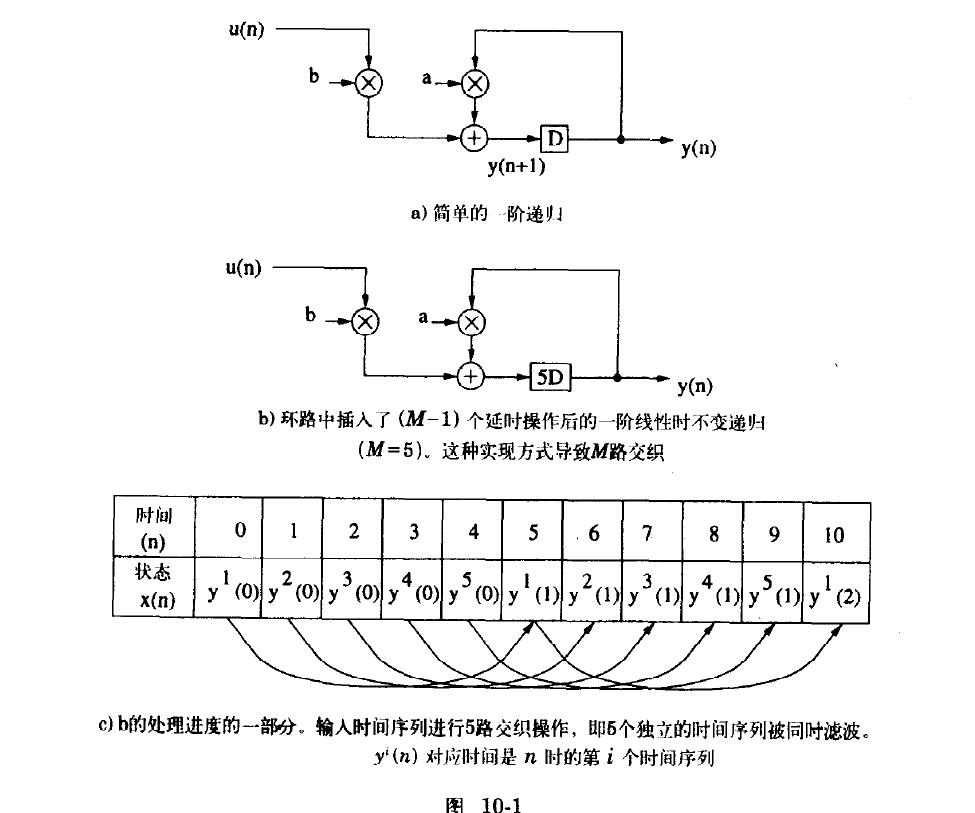
考虑一阶线性时不变递归表达式
y
(
n
+
1
)
=
a
y
(
n
)
+
b
u
(
n
)
y(n+1)=ay(n)+bu(n)
y(n+1)=ay(n)+bu(n)
其实现结构如图10-1 a),如果只有一个延时单元的递归环路,通过插入(M-1)个额外的延时单元实现了M级流水线(图10-1 b),虽然迭代边界减小为1/M,时钟周期可缩短为1/M,但每个数据需要M个时钟周期去处理,并没有对吞吐率带来提高(即M倍降速)。那么输入数据可以进行M路交织操作,即M个独立的时间序列滤波,尽管在低速下滤波,但硬件结构得到了充分利用,如图10-1 c)。
2.2 高效的单通道交织
超前变换,通过递归关系的变换可以把
y
(
n
+
2
)
y(n+2)
y(n+2)表示成
y
(
n
)
y(n)
y(n)的函数产生并行性。
y
(
n
+
2
)
=
a
[
a
y
(
n
)
+
b
u
(
n
)
]
+
b
u
(
n
+
1
)
=
a
2
y
(
n
)
+
a
b
u
(
n
)
+
b
u
(
n
+
1
)
y(n+2)=a[ay(n)+bu(n)]+bu(n+1) =a^2y(n)+abu(n)+bu(n+1)
y(n+2)=a[ay(n)+bu(n)]+bu(n+1)=a2y(n)+abu(n)+bu(n+1)
M-1步超前计算可以表示为
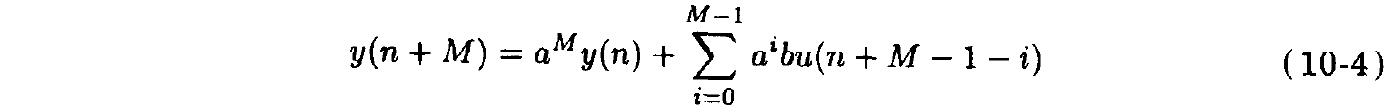
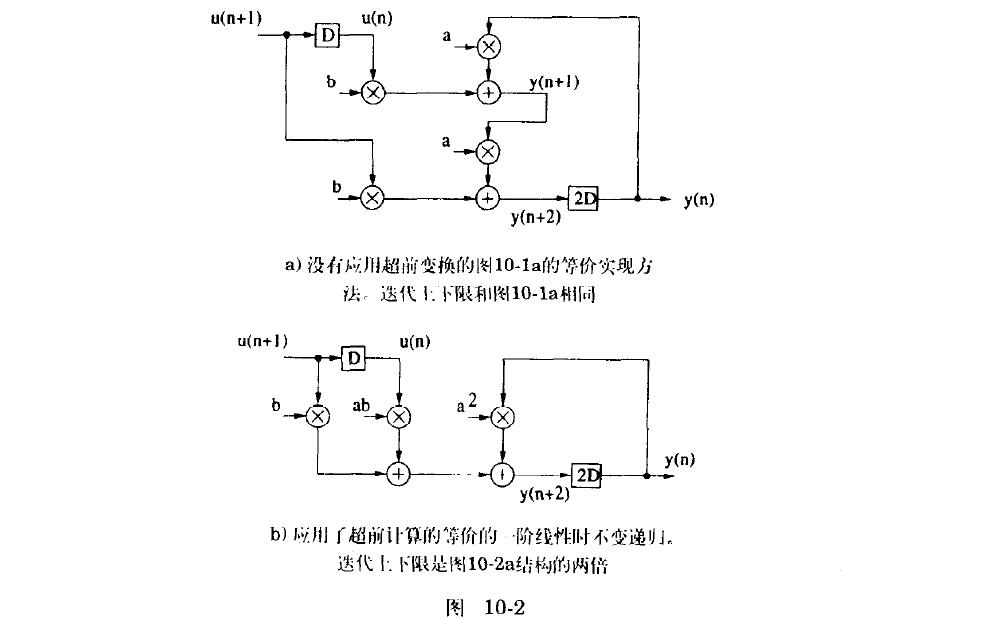
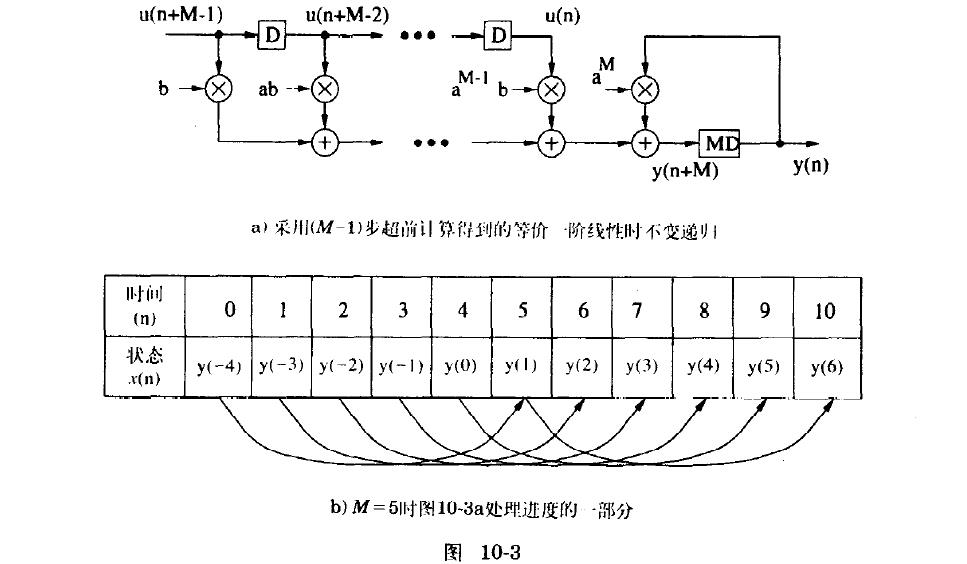
超前计算允许把单一串行的计算变换成M个独立的并行计算,并且把反馈回路用流水线实现,在保持对硬件有充分利用率的同时达到了对单一时间序列的高速滤波。(即不需要多路独立的序列交织,只需要一路序列的初始值初始化寄存器,如y(-4)……y(0),就可以将一路序列相邻5元素分为周期的多路交织)
2.3 高效率的多通道交织
超前计算多路通道相同滤波时,如2通道(时间序列)与递归环路中有6级流水线情况。无超前计算时,只利用了三分之一硬件。迭代两次递归公式,两个时间序列会交织在一起并充分利用了硬件。一般的,若有P个独立时间序列,环路流水线是M级(假设M=PQ),那么递归需要被迭代Q-1次。
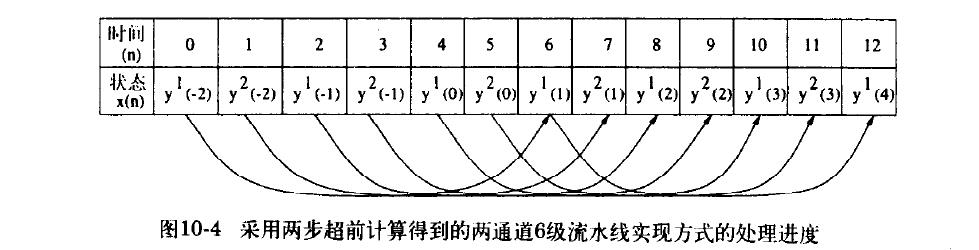
三. 一阶IIR数字滤波器中的流水线实现
本节介绍了使用超前计算技术在一阶递归数字滤波器中实现流水线的方法。
流水线的实现要求环路流水线级数的复杂度线性增长,这里用分解技术实现由于超前处理而产生的非递归部分,以此获得对于环路流水线级数而言硬件只是呈对数增长的实现方式。分解技术是得到面积优化的实现方式的关键,并使得流水线对于高速VLSI IIR滤波器的实现颇具吸引力。
3.1 一阶IIR滤波器的超前流水线结构
超前流水线的基本思想是给传输函数添加可以相消的极点和零点以使传输函数的分母中
z
−
1
,
…
,
z
−
(
M
−
1
)
z^{-1},…,z^{-(M-1)}
z−1,…,z−(M−1)的系数非零。
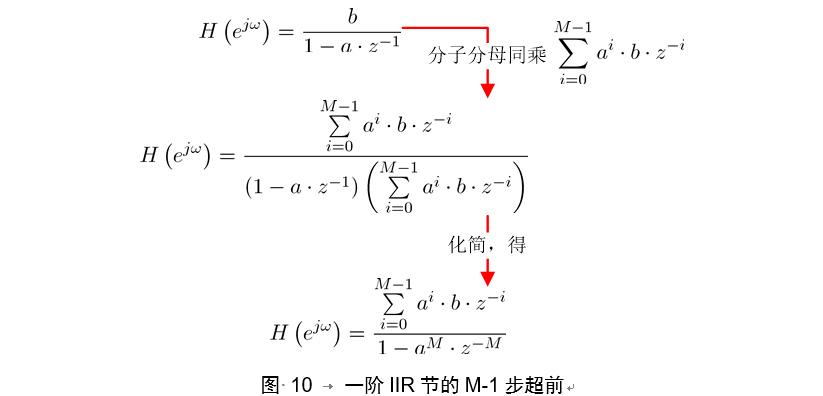
输出采样y(n)可以利用输入和输出采样y(n-M)来计算,这样关键环路就会有M级延迟单元,之后就可以对关键环路进行流水线操作,滤波器的采样频率就会增加M倍。

3.2 在2的幂次分解中实现超前流水线
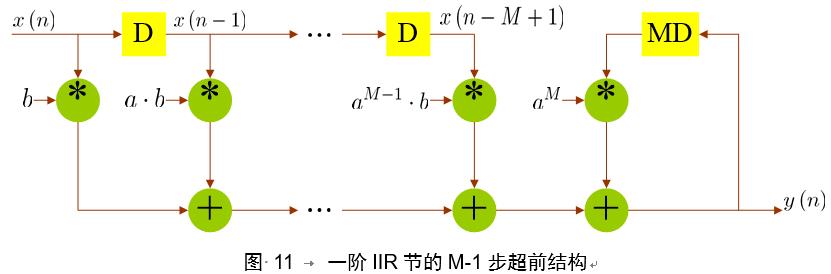
使用超前流水线结构后,传输函数的分子变复杂了,原始迭代方程分子为b,消耗一个乘法器,现在为了抵消分母新增的极点,分子变为
∑
i
=
0
M
−
1
a
i
b
z
−
i
\\sum_{i=0}^{M-1}a^ibz^{-i}
∑i=0M−1aibz−i,消耗M个乘法器和M-1个加法器、延时器。下图为加入超前流水线后的IIR。
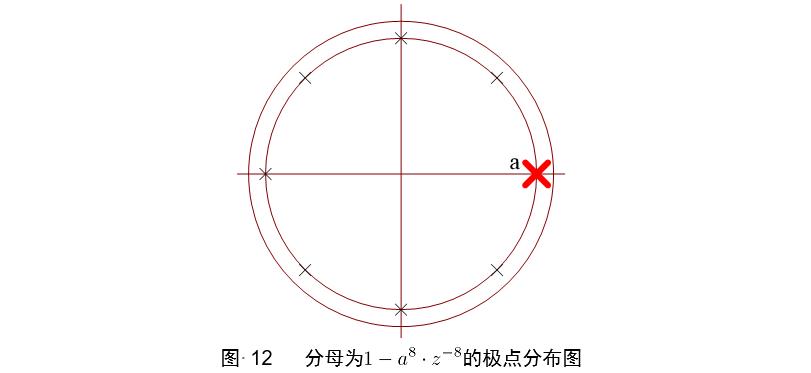
从z域分析可更清楚超前流水线的原理:
对于一阶IIR,分母从
1
−
a
z
−
1
1-az^{-1}
1−az−1变为
1
−
a
M
z
−
M
1-a^Mz^{-M}
1−aMz−M ,表示为圆r=a上等间隔的M个极点,红色为原始极点,黑色为使用超前流水线后增加的极点。
对应于新增的极点,产生相应的零点(用于抵消新增极点的影响),直接实现为
∑
i
=
0
M
−
1
a
i
z
−
i
\\sum_{i=0}^{M-1}a^iz^{-i}
∑i=0M−1aiz−i,蓝色为使用超前流水线后新增的零点。
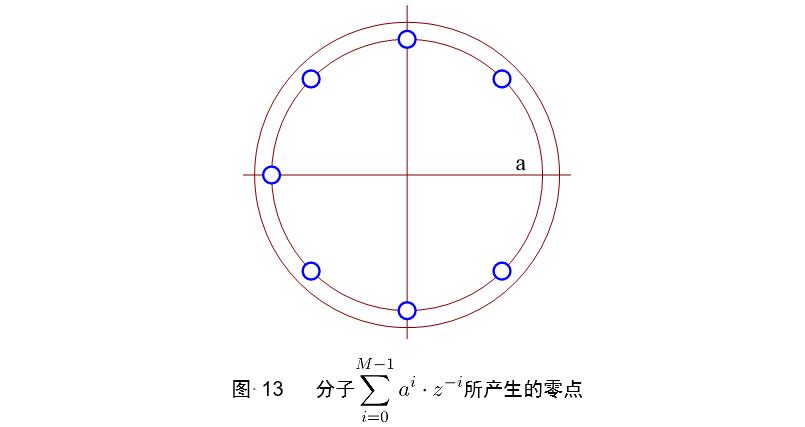
零点分解节约非递归资源:
使用超前流水线产生的分子需要M个乘法器,M-1个加法器和延时单元。直接实现噪声敏感度高,一般采用级联实现,将以上零点恰当的组合就能获得节约面积的结构,一般选择正多边形分解法,如下图所示。
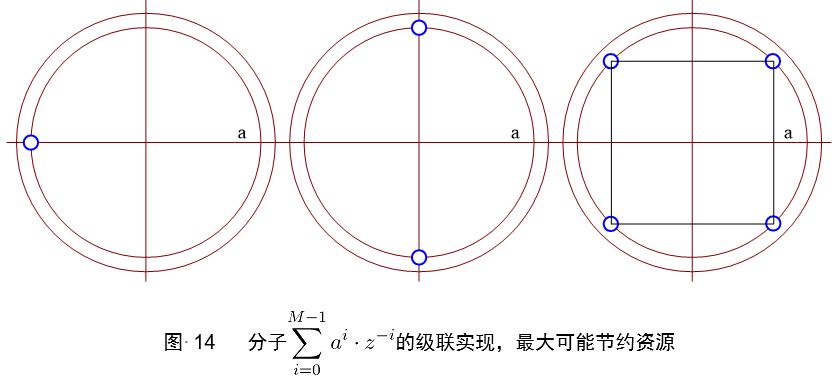
分解后使用超前流水线结构的IIR滤波器传输函数框图如下:

3.3 在通用分解中实现超前流水线
分解的思想可以扩展到任意环路流水线技术,只需要把为了抵消分母的新增分子因式分解即可实现通用分解。

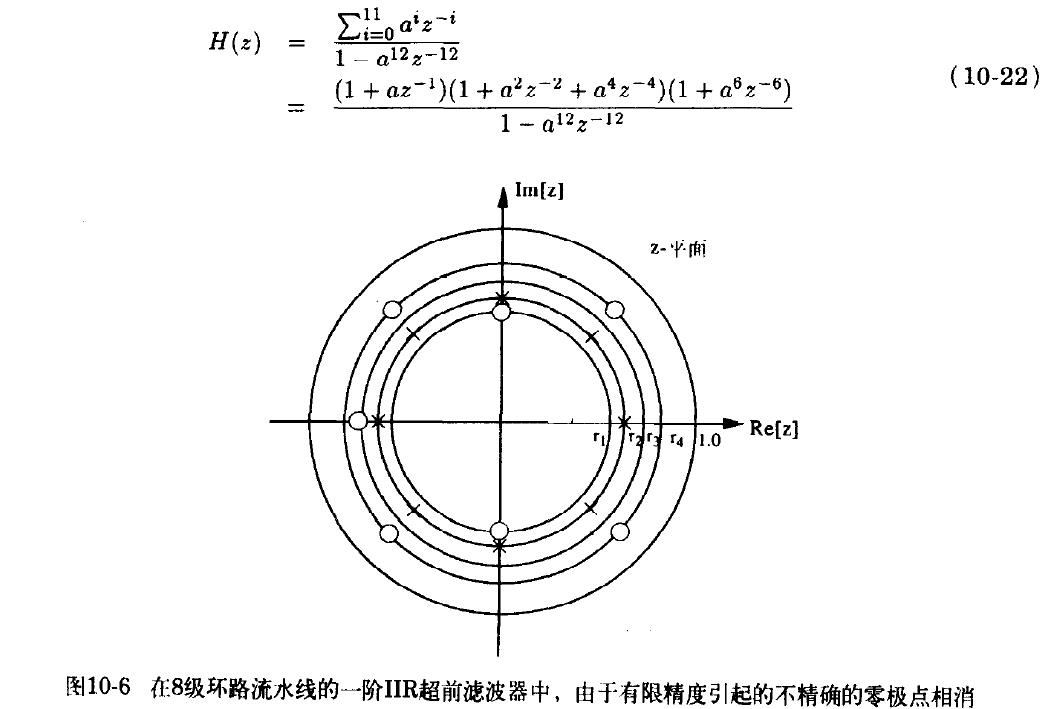

四. 高阶IIR数字滤波器中的流水线实现
这一节介绍使用聚类和离散超前技术在高阶递归数字滤波器中实现流水线的方法(对于一阶IIR滤波器,这两种方法变为同一种形式)。聚类超前流水线要求环路流水线级数线性增长,且不能保证总是稳定。离散超前流水线可获得稳定的流水线滤波器。高阶IIR滤波器也使用分解技术来得到面积优化的高阶滤波器。

4.1 聚类超前流水线
聚类超前流水线基本思想是给滤波器的传输函数添加可以相消的极点和零点,以便使传输函数分母中
z
−
1
,
…
,
z
−
(
M
−
1
)
z^{-1},…,z^{-(M-1)}
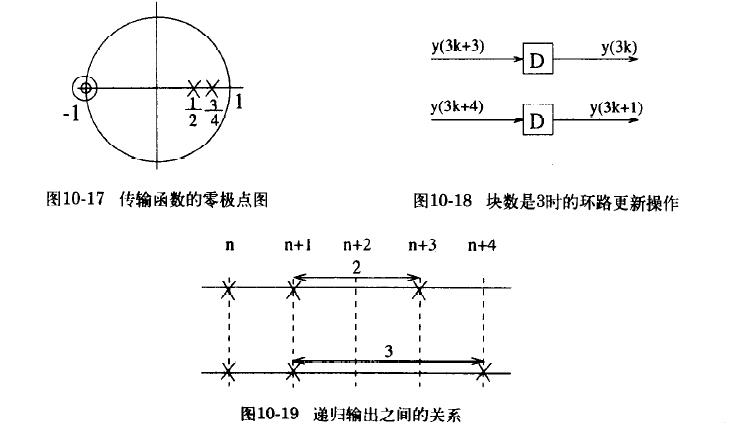
z−1,…,z−(M−1)的系数是0。关键环路中包含了M个延时单元和一个乘法操作,(即环路中连续M个延时串在一起,中间无引出,形成了M级流水线,环路的总延时数可能比M多,多出的是多环路中不属于关键环路的延时,下题可以如此理解)采样率可以提高M倍。这种实现方式叫做M级聚类超前流水线。

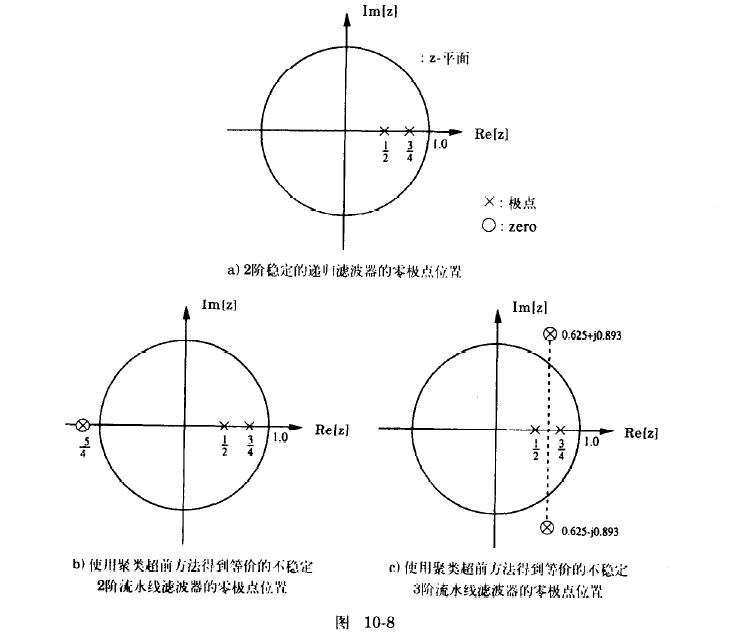
注意,聚类超前引入的相消零极点可能是不稳定的。
N阶M级流水线滤波器的分子或非递归部分可以用(N+M)个乘法运算实现,分母或递归部分可以用N个乘法运算实现,总复杂度是(N+N+M)个乘法运算,和流水线级数、提高的速度或采样率的提高都是线性关系。
4.2 稳定的聚类超前滤波器设计
如果流水线延时级数M不能产生一个稳定的滤波器,那么应该增大M的值,直到滤波器稳定为止。为了得到最佳M值,使用了数值搜索方法,在此不赘述。
4.3 离散超前流水线
离散就是在高阶IIR滤波器传输函数添加可以相消的极点和零点,以便使传输函数分母的项从原来的 z − 1 , z − 2 , … , z − N z^{-1},z^{-2},…,z^{-N} z−1,z−2,…,z−N变换为 z − M , z − 2 M , … , z − N M z^{-M},z^{-2M},…,z^{-NM} z−M,z−2M,…,z−NM的项。分母各项之间阶数间隔为M。
区别于聚类超前流水线,离散超前流水线设计总是稳定(前提是原滤波器是稳定的),但是离散超前可能会耗费更多的资源(包括乘法器,加法器和延时)。

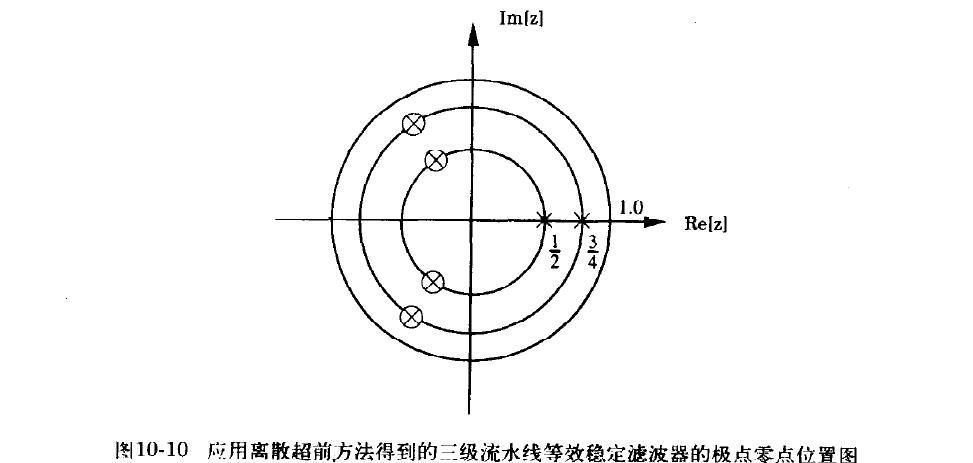
对于原滤波器每一个极点,引入(M-1)个相消的极点和零点,这些极点和零点有相同的角度,到原点的距离和原极点相同,所以滤波器总是稳定的。
使用离散超前流水线,非递归部分的乘法复杂度是(NM+1),递归部分乘法复杂度是N,总的复杂度是(NM+N+1)个流水线乘法,和流水线级数M成线性关系。
4.4 基于2的幂次分解的离散超前流水线

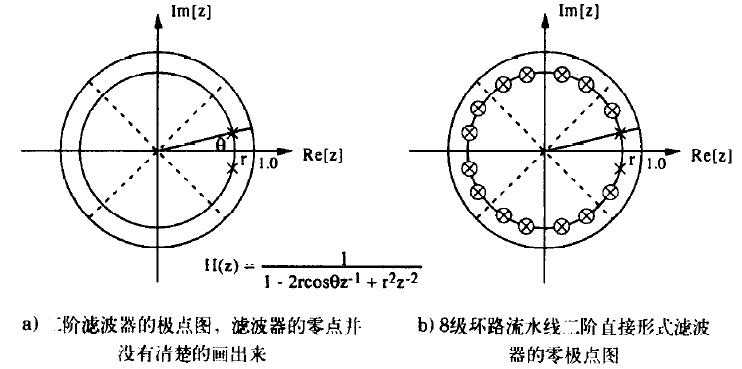
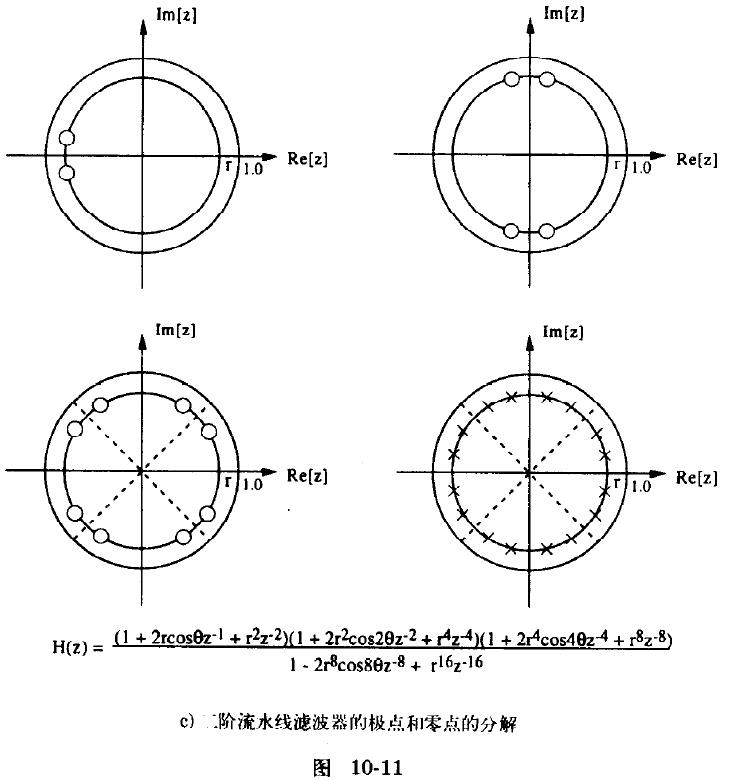
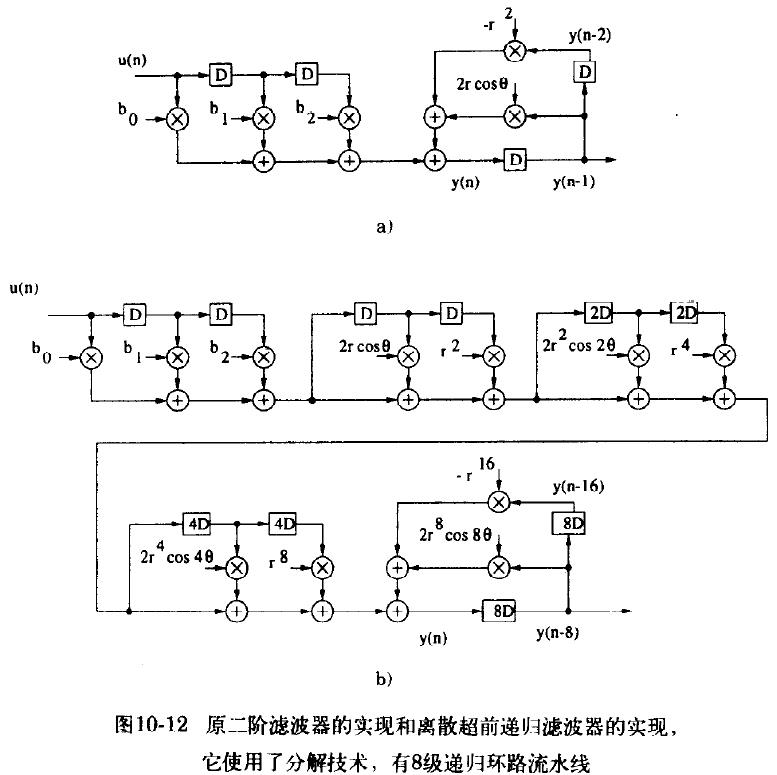
4.5 在通用分解中实现离散超前流水线

4.6 受限的滤波器设计技术(略)
五. IIR滤波器的并行处理
回顾第三章的并行处理设计方法,L路并行,就是将n=kL+i,其中i=0,…,L-1, 代入原始迭代公式,以一阶IIR为例,迭代公式为:
y
(
n
)
=
a
y
(
n
−
1
)
+
b
x
(
n
)
y(n)=ay(n-1)+bx(n)
y(n)=ay(n−1)+bx(n)
设计三并行结构,L=3,如下:
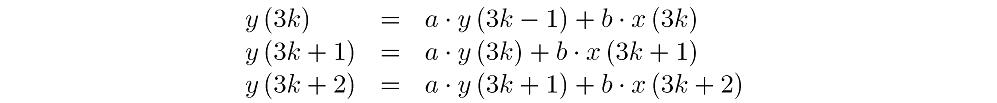
电路架构如下所示:
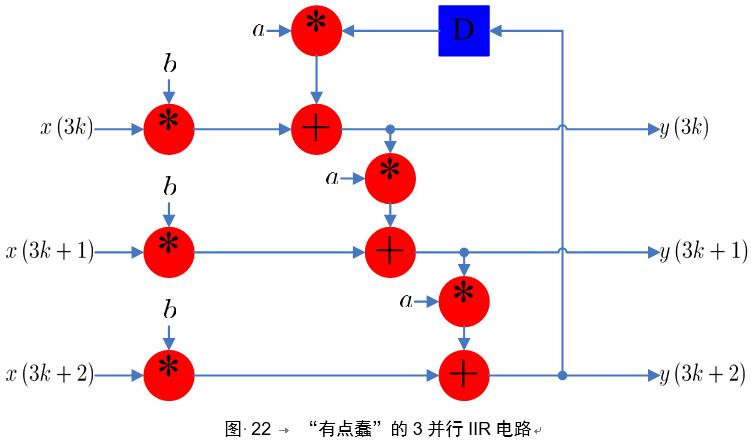
每一个输出点都依赖于其前一个输出点,也就是在输出点之间形成了一个串行的“进位链”,从这一点上说该电路不能算是并行处理。
超前计算可以实现完全的并行处理,对原始公式进行2步超前迭代得:
y
(
n
)
=
a
3
y
(
n
−
3
)
+
b
x
(
n
)
+
a
b
x
(
n
−
1
)
+
a
2
b
x
(
n
−
2
)
y(n)=a^3y(n-3)+bx(n)+abx(n-1)+a^2bx(n-2)
y(n)=a3y(n−3)+bx(n)+abx(n−1)+a2bx(n−2)
表示成并行迭代式,如下:
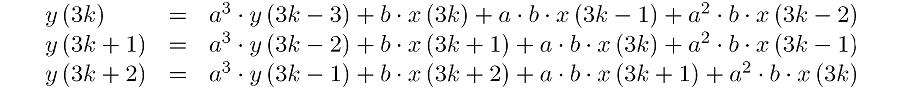
电路架构如下图:
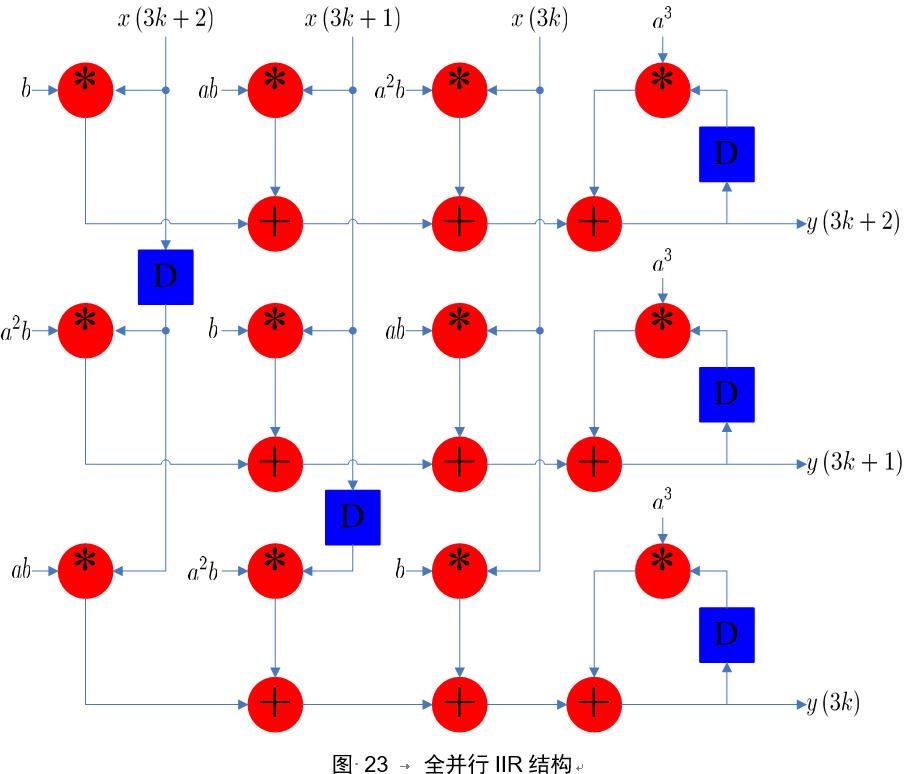
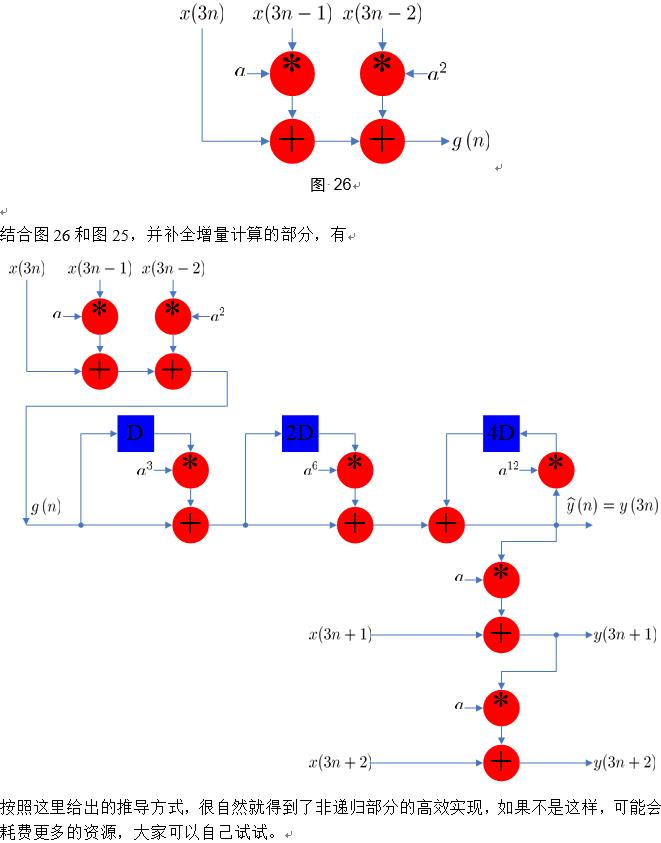
全并行IIR结构消耗的资源非常多,将图22与图23结合起来,可以得到一个折中的结构,其中存在增量技术,即每一个输出点都依赖于其前一个输出点,称为增量块滤波器结构,如下图所示:
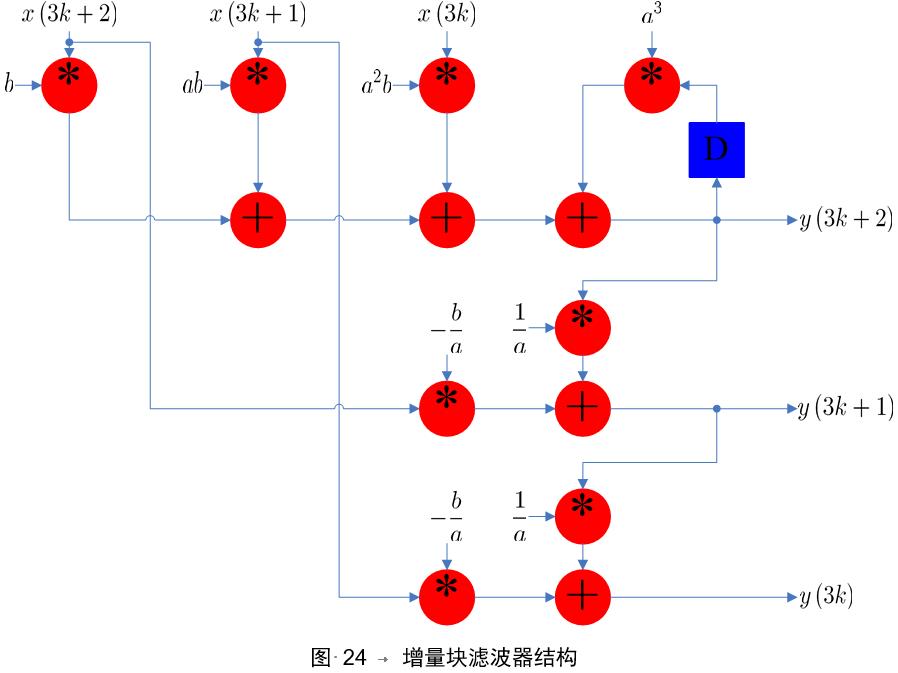
例:


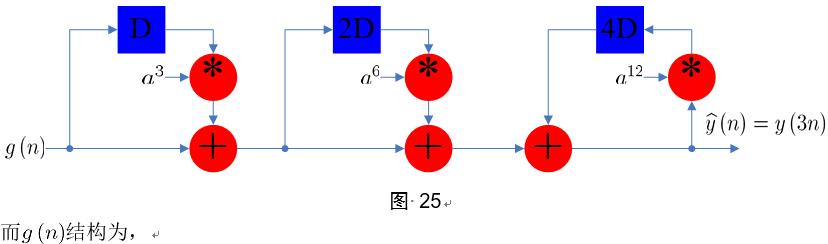
一般地,对N阶IIR滤波器来说,它的L级增量并行处理结构可以分两步得到:
- 先使用由聚类超前技术得到的环路更新方程独立地计算前N个输出采样y(Lk),y(Lk+1),…,y(Lk+N-1);
- 利用得到的前N个输出采样,增量计算剩下的L-N个采样y(Lk+N),…,y(Lk+L-1)。注意当L<N时,增量计算技术就不适用了。
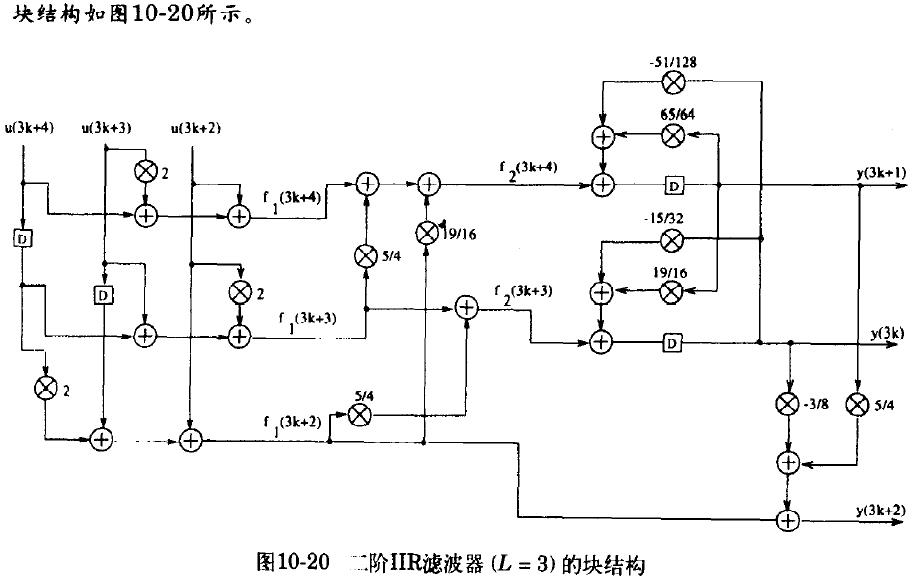
六. 组合了流水线和并行处理的IIR滤波器
IIR滤波器中,把流水线和并行处理组合起来,可以使采样率提高L×M倍或者在同样的采样率下降低功耗,其中L是块处理的个数,M是流水线的级数。总原则是“先并行,后流水”。
例:

七. 利用流水线和并行处理的低功耗IIR滤波器设计(略)
八. 流水线自适应数字滤波器(略)
8.1 弛豫超前变换
8.2 流水线LMS自适应滤波器
8.3 用流水线实现随机梯度格型结构
九. 结论
本章中,首先,应用聚类超前和离散超前流水线的方法在一阶和高阶IIR数字滤波器中实现了流水线。其次,还用增量块处理技术来设计具有小面积开销的并行IIR滤波器。最后,结合超前流水线技术和增量块处理技术实现了递归IIR滤波器的流水线与并行处理。
附:离散超前流水线IIR滤波器的传输函数推导(matlab)
%设置原始IIR滤波器阶数N和流水线级数M
M = 6;
N = 2;
K = M*N;
%输入原始IIR滤波器传输函数分母Dz(其中p=z^(-1))
syms p
Dz = 1-0.6*p+0.25*p^2;
%输入IIR滤波器需要的新增分子分母同乘多项式Pz,Pz最高次为K-N,未知系数为ai,目的是求解此系数
syms a1 a2 a3 a4 a5 a6 a7 a8 a9 a10
Pz = 1+a1*p+a2*p^2+a3*p^3+a4*p^4+a5*p^5+a6*p^6+a7*p^7+a8*p^8+a9*p^9+a10*p^10;
%Dz与Pz相乘且合并同类项得到离散超前流水线传输函数的分母DP
DP = collect(Dz*Pz,p);
%取出DP由低次到高次的系数向量为coe
coe = coeffs(DP,p);
%建立方程组eqns,DP的k*M次项(k=1…N)系数不为零,其余系数均为零
eqns = [coe(2)==0,coe(3)==0,coe(4)==0,coe(5)==0,coe(6)==0,coe(8)==0,coe(9)==0,coe(10)==0,coe(11)==0,coe(12)==0];
%求解方程组得到解为S,将解带回DP与Pz,得到离散超前流水线IIR滤波器的分母DP与分子Pz
S = solve(eqns,[a1 a2 a3 a4 a5 a6 a7 a8 a9 a10]);
DP = subs(DP,[a1,a2,a3,a4,a5,a6,a7,a8,a9,a10],[S.a1,S.a2,S.a3,S.a4,S.a5,S.a6,S.a7,S.a8,S.a9,S.a10]);
Pz = subs(Pz,[a1,a2,a3,a4,a5,a6,a7,a8,a9,a10],[S.a1,S.a2,S.a3,S.a4,S.a5,S.a6,S.a7,S.a8,S.a9,S.a10]);
%将分子Pz因式分解用于离散超前流水线的后续分解
Nz = factor(Pz);
以上是关于VLSI数字信号处理系统——第十章流水线结构的并行自适应递归滤波器的主要内容,如果未能解决你的问题,请参考以下文章