VLSI数字信号处理系统——第六章折叠

Posted 2021-06-06 夏风喃喃

VLSI数字信号处理系统——第六章折叠

作者：夏风喃喃
参考：
(1) VLSI数字信号处理系统:设计与实现 （美）Keshab K.Parhi／著
(2) socvista https://wenku.baidu.com/u/socvista?from=wenku

文章目录

• VLSI数字信号处理系统——第六章折叠
• • 一.引言
  • 二.折叠变换
  • 三.寄存器最小化技术
  • • 3.1寿命分析
    • 3.2采用前向-后向寄存器分配的数据分配技术
  • 四.折叠架构的寄存器最小化
  • • 4.1双2次节滤波器例子
    • 4.2IIR滤波器例子（略）
  • 五.多速率系统的折叠（略）
  • 六.结论

一.引言

当对吞吐率要求不高而且系统中存在大量功能相同的节点时，可以考虑使用分时复用的折叠技术，把功能相同节点折叠成一个节点或几个节点来达到缩减资源占用的目的。折叠之后的系统结构要想保持原有功能不变，必然要加入一定量的寄存器资源用于存放中间计算结果，以及控制逻辑（包括状态机和选路器等）。本章给大家介绍的是一种极为通用的折叠技术，能把系统中功能相同的节点折叠成一个节点，不仅给出如何来构造控制逻辑的方法，还进一步优化寄存器资源的使用。

二.折叠变换

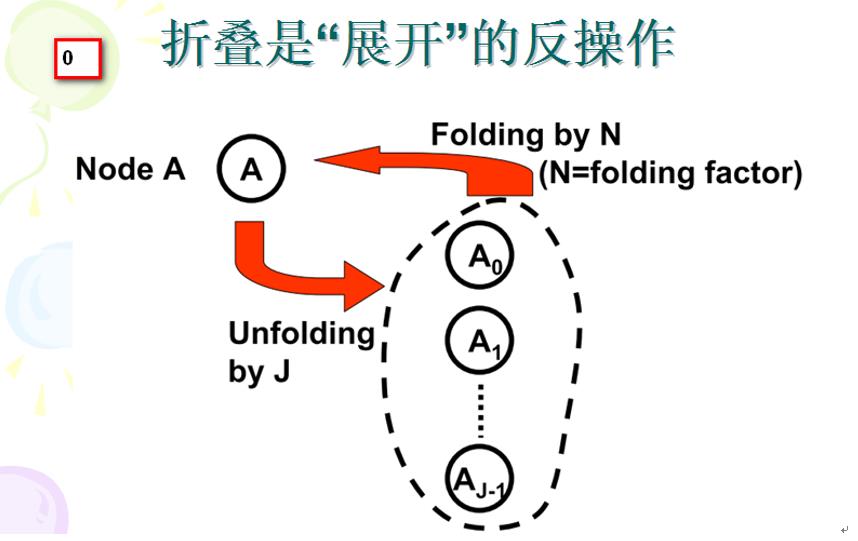
假设原始DFG有J个A运算节点，也就是说在一次迭代中需要同时（并行地）进行J个A运算。现在为了节约资源，在硬件电路上只设立一个A节点，但要求这个被折叠之后的DFG保持原始DFG功能不变。

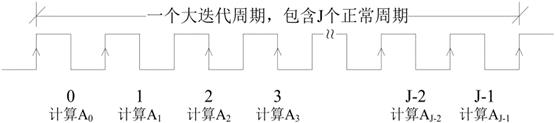
对于原始 DFG ，一次迭代要进行J个A运算，折叠后的DFG需要迭代J次才能完成原始DFG迭代1次的计算。折叠后的DFG以J个正常的周期作为一个大迭代周期。折叠后的DFG需要J次迭代才能完成原始DFG一次迭代的计算，吞吐率降低很多，但是要注意不一定是降低J倍，因为折叠后DFG 关键路径往往会更短，可以运行在更高的时钟频率上。

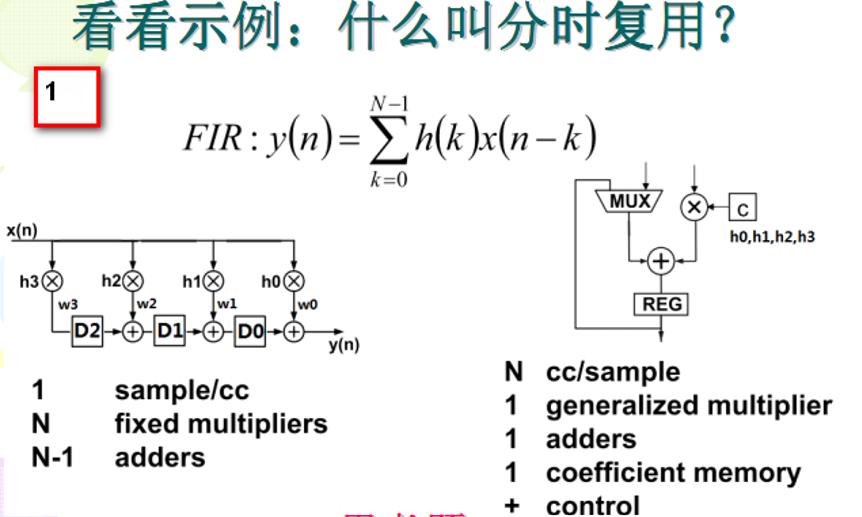
在幻灯片1中，左侧4个乘法节点折叠为1个乘法节点，3个加法节点折叠为1个加法节点。
折叠集：
幻灯片1的原始DFG存在两个折叠集， 4个乘法器构成一个折叠集， 3个加法器构成另一个折叠集。必须往加法折叠集中添加一个空节点（不起实际作用的节点），以使得加法折叠集与乘法折叠集具有相同数目的节点。乘法折叠集为{M0,M1,M2,M3}，加法折叠集为{A0,A1,A2,O}，
折叠因子：
折叠集元素个数，表征折叠的强度。
折叠序数：
每个折叠集中的节点都有唯一不同的序号，这些序号也称为折叠序数，表示该节点在大迭代周期的第几个子周期被计算。比如乘法折叠集{M0,M1,M2,M3}和加法折叠集 {A0,A1,A2,O} ，意味着在大迭代周期的第0 个子周期将执行M0和A0的计算，第1个子周期执行M1和A1的计算，第2个子周期执行M2和A2的计算，第3个子周期执行M4和O的计算。折叠集中节点的次序由设计人员安排，不同的次序可能会得出不同性能的电路。

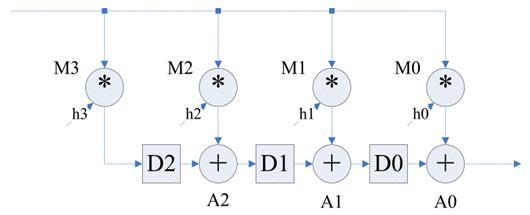
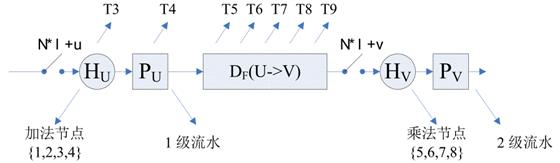
选定了折叠集和规定折叠集节点的次序之后，就可以动手构造折叠之后的DFG了。如下图所示，假设要对原始 DFG 进行N阶折叠，并且已经规定将原始DFG中的U节点折叠到新DFG的$H_u$节点的第N*l+u周期执行；V节点被折叠到新DFG的$H_v$节点的N*l+v周期执行。原始 DFG 中包含多个乘法节点和加法节点（见上图），四个乘法节点{M0,M1,M2,M3}被折叠到$H_u$的不同子周期执行，“四个”加法节点{A0,A1,A2,O}被折叠到$H_v$的不同子周期执行。

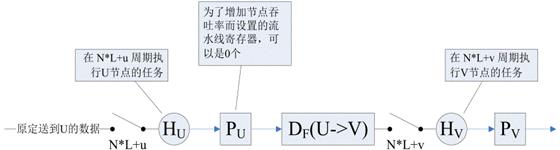
因为原始 DFG 中的乘法节点和加法节点之间可能存在通路（带延时或不带延时），对于原始DFG中每一条边，必须在折叠后的DFG中构造相应的带有选通开关的边，才能保证折叠前后的两个DFG功能一致。

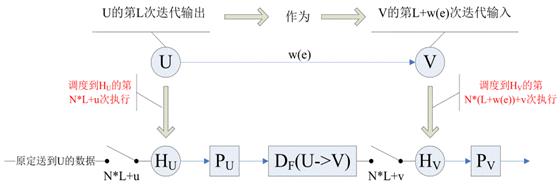
上图详细给出了原始 DFG 中 U->V 延时 w(e) 的边与折叠后 DFG 需要构造的新边的对应关系，下一步只需求出 $P_U$ 和 $D_F(U->V)$ 的数值，新边构造就完成了。列出 $P_U$ 和 $D_F(U->V)$ 的计算公式，如下：

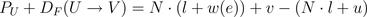
化简后有

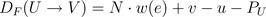
注意，折叠后 DFG 是可以在计算节点上引入流水线寄存器$P_U$的，当然也可以不引入 ，但是如果计算节点可以设计成流水线结构，显然可以进一步提高时钟频率，从而增加系统吞吐率，这就是折叠变换优势的地方（ N阶折叠后的DFG完成任务所需的迭代次数为原始DFG的N倍，但是从绝对时间上看，不一定是N倍，往往少于N倍，因为可以利用流水线技术了使运行频率可以更高 ）。

例：
下面以幻灯片10的双2次节滤波器为例，左图为原始结构图，右图为重定时之后的结构图。 重定时可以在很多情况下消除折叠违例的情况，即消除折叠变换后路径延时出现负数的情况。（重定时的方法后面描述）

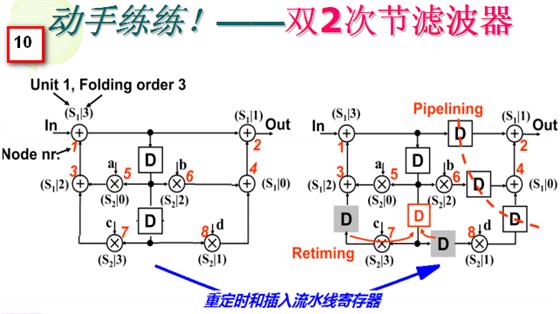
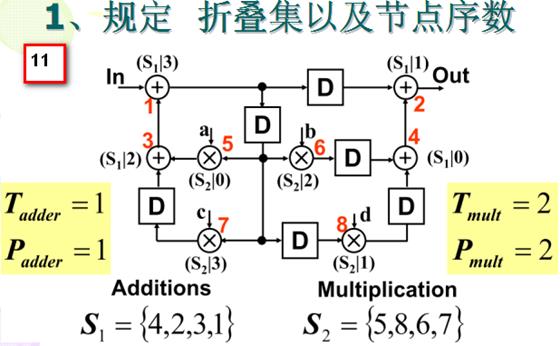
1. 定义折叠集以及其元素的次序。
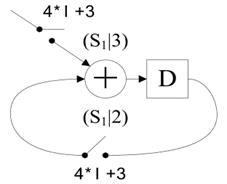
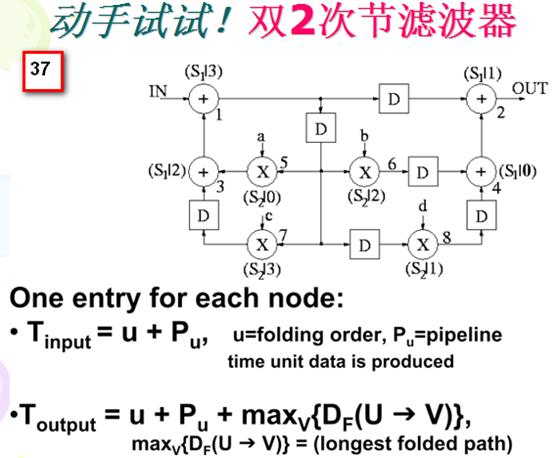
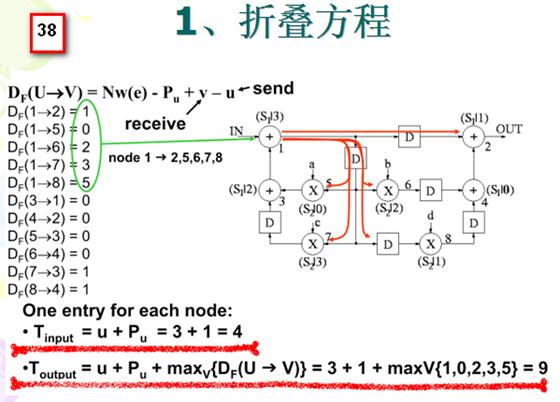
对于幻灯片10右图的DFG乘法节点和加法节点各4个，乘法节点运算时间为2u.t.，加法节点运算时间为1u.t.。4 个加法节点形成一个折叠集S1，4个乘法节点形成一个折叠集S2，然后在加法节点上安插1个流水线寄存器，成为1级流水加法，在乘法节点上安插2个流水线寄存器，使得乘法节点成为2级流水乘法器。折叠集中节点次序如右图所标注，比如节点 1 （红色数字）是加法节点，它属于折叠集S1，且序号为3，所以记为(S1|3) ，再如节点8是乘法节点，它属于折叠集S2，且序号为1，所以记为(S2|1) 。

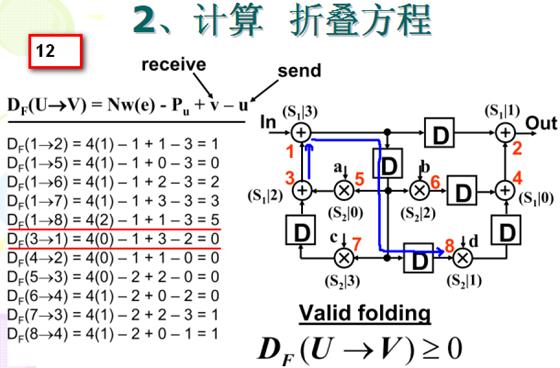
2. 计算折叠方程：
对于原始 DFG 中的每一条边，都要计算其折叠方程，注意这里有乘法节点流水线寄存器 $P_m=2$ ，加法节点流水线寄存器 $P_a=1$ ，采用 4 阶折叠 N=4 。若乘法节点为起始节点，折叠方程为 $N\ast w(e)+v-u-P_m$ ；若加法节点为起始节点，折叠方程为 $N\ast w(e)+v-u-P_a$ 。

3. 验证$D_F(U->V)$非负：
负延时是不可实现的，也就是说只要所有折叠方程的结果非负，那么这个折叠变换就是可以进行的。

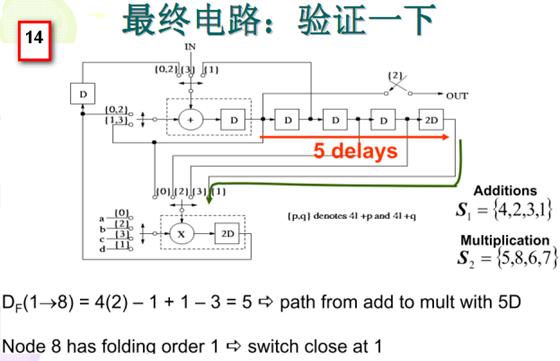
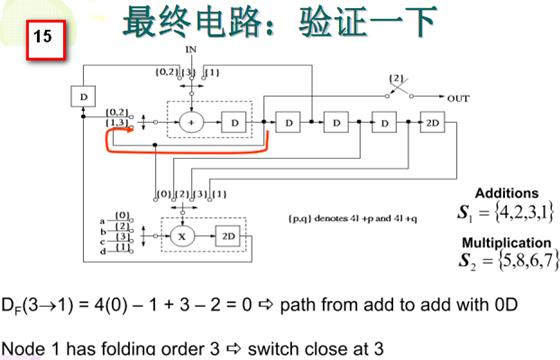
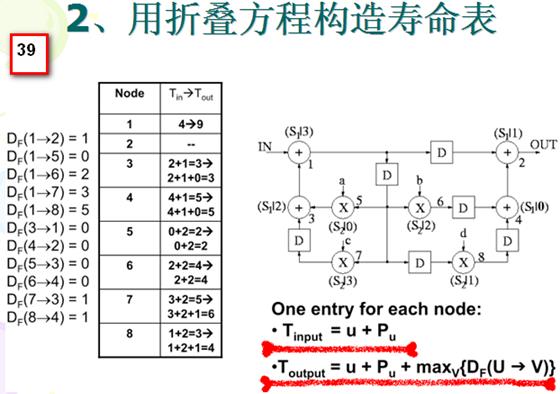
4. 画出折叠后的电路：
根据折叠方程画出最终的电路图也并非易事，需要仔细思考。




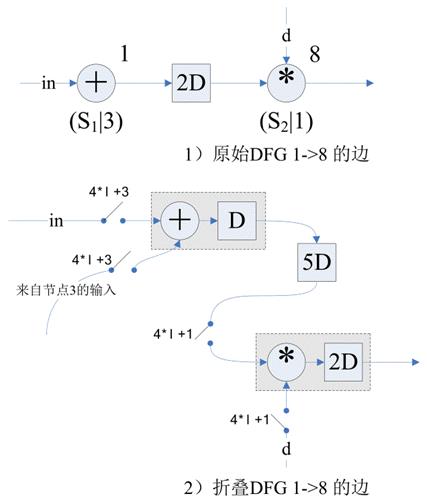
5. 折叠前的重定时：
重定时可以在很多情况下消除折叠违例的情况，那么最理想的折叠变换应该与重定时结合在一起。根据重定时方程的定义：

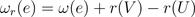
只需将折叠方程中的 $w(e)$ 替换为重定时之后的 $w_r(e)$ 即可得到重定时版本的折叠方程，如下：

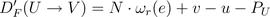
为了保证没有负延时边出现，必须满足以下不等式条件：

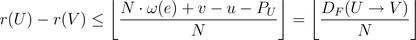
只需保证由所有折叠方程导出的线性重定时不等式组有解，就可以求出具体的 $w_r(e)$ ，从而算出 $D{’}_F(U->V)$ ，然后即可画出最终的折叠电路。

三.寄存器最小化技术

折叠之后的新电路多出很多延时。延时在硬件电路中对应寄存器，是一种比较昂贵的资源。直接画出的折叠电路的寄存器资源往往是冗余的，只使用其中一部分就能保证中间数据的正确存储而不影响电路功能，但是寄存器资源的减少所需付出的代价是需要额外的控制电路和选路器等。

3.1寿命分析

在介绍寄存器寿命分析之前，首先来看看中间数据产生后是如何存储到寄存器中去的。以上升沿触发的 DSP 系统为例：

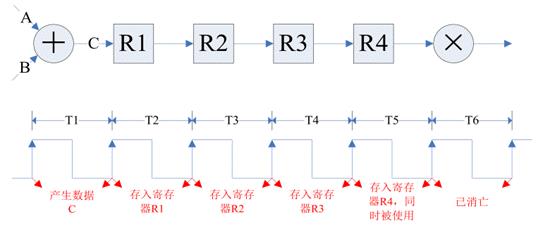
上图清楚的说明了，中间数据（比如C），在产生之时（T1）不占用寄存器，从产生后的一个周期（T2）到被使用的周期（T5）占用寄存器。

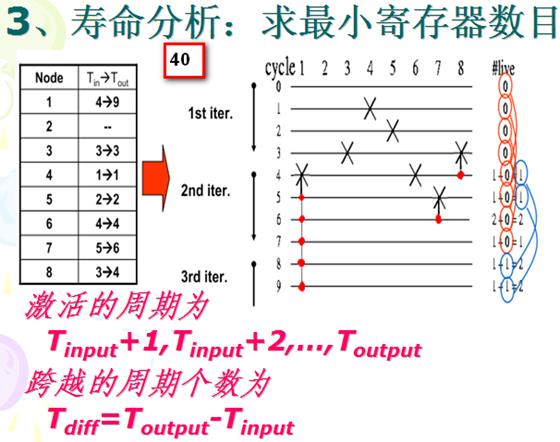
激活：一个样值（也称为变量）从产生之后的第一个周期到被应用的周期是激活的，样值被应用后就消亡了。样值在它激活的每一个周期都要占据一个寄存器。

寿命分析：分析每一个中间变量的激活周期，以确定 DSP 系统中最大的激活变量数目，最大的激活变量数目也就是系统正常工作所需的理论最小寄存器数目。寿命分析有两种图形技术：线性寿命图和循环寿命图。两者是等价的。

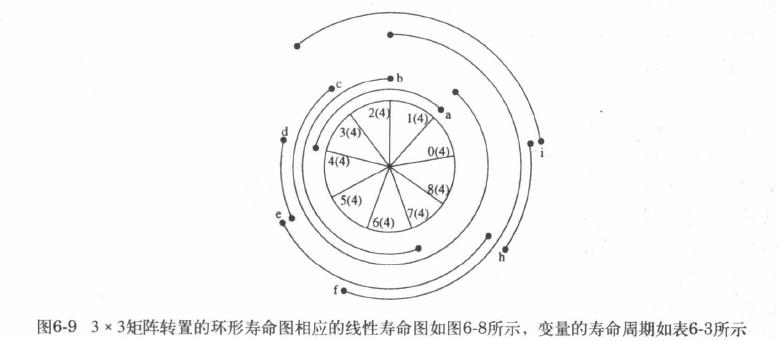
3.2采用前向-后向寄存器分配的数据分配技术

步骤：

1. 通过寿命分析确定最小寄存器数目
2. 以 3x3 矩阵转置为例，在寿命期开始所对应的时间步输入每个变量，如下表 input 列；如果在给定周期里有多个输入变量，这些变量就分配到多个不同的寄存器，原则是寿命越长的变量所分配的寄存器越靠前，寿命越短的变量所分配的寄存器越靠后（靠近出口）。
3. 每个变量都以这种前向的方式分配，直至变量消亡或者达到末尾寄存器。前向分配的是指，如果变量 a 当前存储在寄存器 i 中，那么下一个周期变量 a 将移动到寄存器 i+1 ，如果寄存器 i+1 不可用，那么变量 a 分配给第一个可用的前向寄存器。
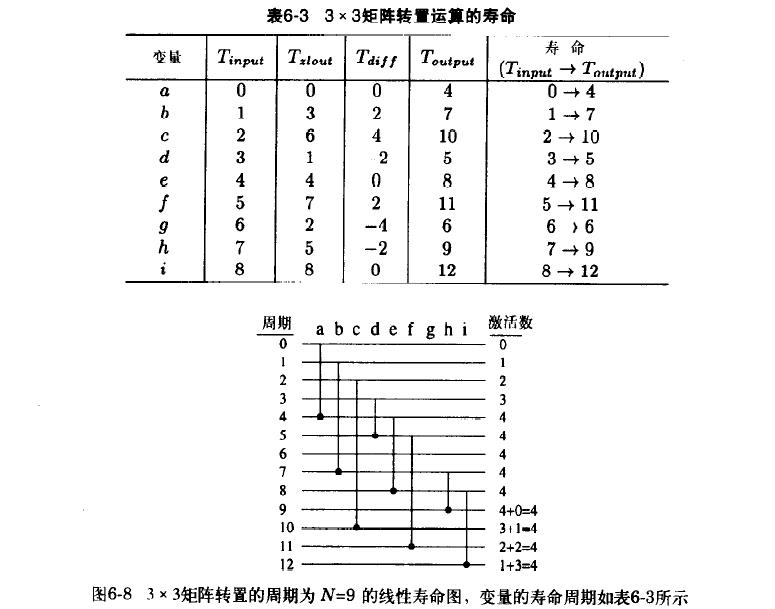
4. 因为分配是周期的，当前迭代 $l$ 的分配在接下来的 $k\ast N+l$ 迭代中会重复，因此，如果 $R_j$ 在迭代 $l$ 被某个变量占据，则 $R_j$ 在所有 $k\ast N+l$ 迭代都被该变量的新版本所占据。如下表 ， N=9 ， R1 在周期 1 被 a 占用，那么 R1 在周期 1*9+1=10 也同样被新版本的 a 所占据，其他的寄存器情况类似。
5. 对于到达末尾寄存器但仍未消亡的变量，可以计算它的剩余寿命，然后基于先到先得的原则，将这些变量以后向的方式分配给寄存器。如果后向分配中有多个寄存器可用，首先尝试选择在末尾寄存器和该寄存器之间已进行过后向分配的寄存器。如果有不止一个寄存器符合后向分配，在候选寄存器中，选择有最少但足够多的前向寄存器来完成变量分配的那个寄存器。一个变量经过后向分配后，再进行前向分配，直至消亡或再次到达末尾寄存器。
6. 按要求重复步骤 4 和 5 直至所有变量分配完成。
   
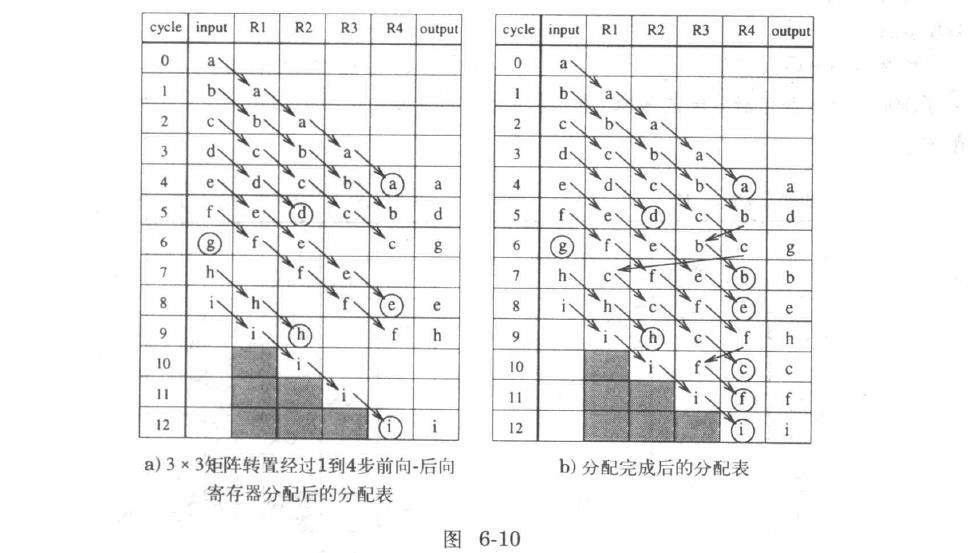
   以 3x3 矩阵转置为例，见上图，先进行所有 9 个变量的前向分配操作。注意，变量 a/d/e/h/i 在前向分配的过程中就消亡了，不需要对其进行后向分配；变量 g 在产生的周期内立即消亡，不需要进行前向后向寄存器分配；在前向分配中未消亡的变量 b/c/f ，需要进行后向分配。
   

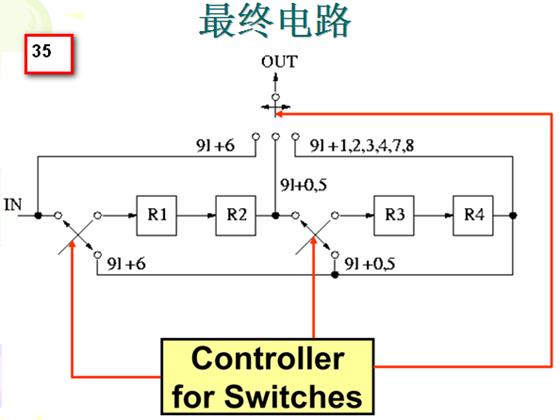
四.折叠架构的寄存器最小化

4.1双2次节滤波器例子

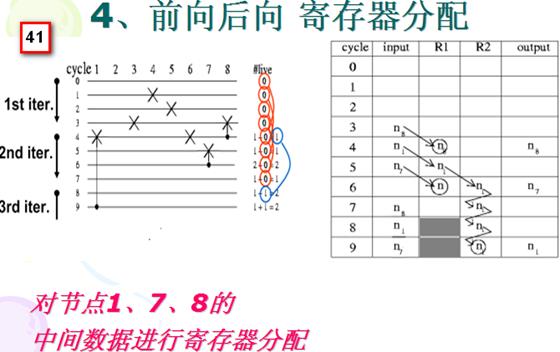
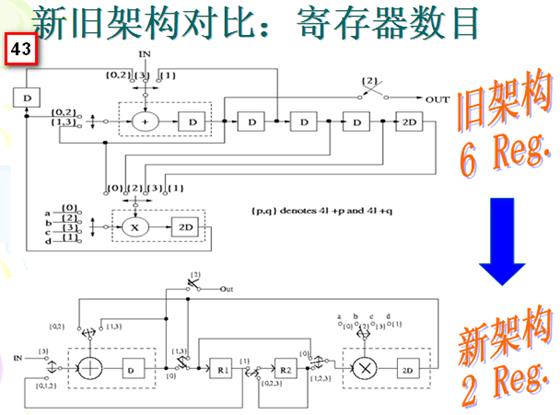
4.2IIR滤波器例子（略）

五.多速率系统的折叠（略）

六.结论

折叠是设计时分复用架构的系统变换技术，虽然折叠电路只需较少的硅面积，但可通过运用功能单元的细粒度流水线以较高的速度运行。折叠集通过任何调度和分配技术设计，可以用来减少折叠电路的存储单元数目。