2021华中杯数学建模赛题思路(更新)

Posted 2021-06-06 微信公众号：您好啊数模君

A 题 马赛克瓷砖选色问题

 

选近似颜色的瓷砖，可以直接用距离公式搞定，matlab中用距离pdist2函数解决，edit pdist2后可以看到有很多种距离公式算法

 

 ​

 

很多小朋友到这里就完事了，其实不然，举个例子，三个颜色矩阵[0.6,0.6,0.6]、[0.5,0.5,0.5]、[0.5,0.6732,0.5]，其中1和3和2欧式距离都相差0.1732距离，依次可视化颜色矩阵后

 

 

可以看出我们还应考虑的是 RGB 差值的方差，例如[0.6,0.6,0.6]与[0.5,0.5,0.5]做差后差 值一样，其方差为 0；[0.5,0.5,0.5]与[0.5,0.6732,0.5]做差后得到[0,1.732,0]，其方差为 1；两 个公式后者作为优先排序条件，前者距离公式作为次要排序条件为宜。（方差为0说明为同种颜色，再次前提下欧式距离越大明暗差别越大），本段描述下面绘制程序。

 

figure % 0-1对应的为0-255

p=plot(1,1,'o','LineWidth',100);%方差为0

set(p,'color',[0.6 0.6 0.6]);

hold on

p=plot(2,1,'o','LineWidth',100);%标准点用于对比

set(p,'color',[0.5 0.5 0.5]);

p=plot(3,1,'o','LineWidth',100);

set(p,'color',[0.5 0.6732 0.5]);%方差不为0，欧氏距离与第一个点一致

axis([0,4,0,2])

 

然而在第一问中，附件2和附件3中如果按上述排序方式选择近似颜色，就会发现，欧式距离过大，但是方差很小，颜色深浅差距很大，因此我们可以设置权重以平衡这两个公式。同样的我们可视化看下。

 

 

figure% 0-1 对应的为0-255

p=plot(1,1,'o','LineWidth',100);%方差为0

set(p,'color',[0.6 0.6 0.6]);

hold on

p=plot(2,1,'o','LineWidth',100);%标准点用于对比

set(p,'color',[0.5 0.5 0.5]);

p=plot(3,1,'o','LineWidth',100);

set(p,'color',[0.5 0.54 0.5]);%方差不为0，欧氏距离与第一个点一致

axis([0,4,0,2])

 

从效果来看还可以接受，两个结果的欧式距离分别是0.1732和0.05，因此我们可以将差的方差和欧式距离公式权重比例设为0.776:0.224，我们新构建的距离公式应当为

 

 

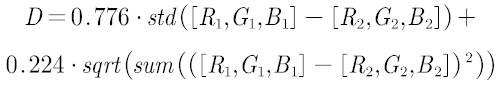
权重可以根据各自认为的颜色近似自行设置，这里只是给了一个案例

 

对于第二问，这个表现力就是说能够近似体现多种颜色，优先增加与多个颜色差别较小，不管增加几种颜色，但本质上还是选近似颜色，只不过同时多增加几种颜色就要考虑新聚类中心的分布问题，FCM思想比较适合解决该问题，目标函数可以就以FCM的来

 

 

 

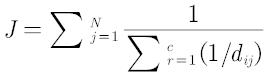
其中i表示聚类中心，j表示其他点，c为聚类中心总数，N为其他点总数，（别去管什么隶属度矩阵，你们直接用上面函数就行，除了FCM也可以借助其他聚类算法的思想来做）

 

该算法思想就是其他点到聚类中心的距离的倒数之和最小，但是别直接套用该算法程序，其中的距离公式需要更改。第二问说是从技术革新的角度，那么本问被聚类的点应当为256*256*256个点了，并不是附件2和附件3的点来做聚类分析，当然在选出新聚类中心颜色后，可以再去算一附件2和附件3的J函数值，对于题目提到的表现力，颜色越近似就说明表现力越好，表现力函数公式可以直接是J函数的倒数。

 

本文的程序设计思路可以做个参考：

1.两个自变量，除了固定的22个颜色外额外增加的颜色数、聚类范围(切记不是半径为R的圆形)

2.(优化算法)随机产生n个个体，每个个体拥有m个新聚类中心(m个RGB值，看做是三维坐标)和1个聚类范围，被聚类的点就是256*256*256个点，按第一问距离公式计算各聚类中心距离。

3.设立目标函数J，如果想将表现力设为目标函数，这里目标函数就设为1/J。（第一问两个公式加权聚合为一个公式，权重自行设立，效果不好就调试下)，求J函数最小化或者1/J函数最大化。

4.迭代多次后，输出新增最佳m个颜色RGB。

 

第三问，在上一问基础上考虑成本，成本函数就按新增了多少个颜色来算，相当于说本问寻优的自变量个数m是变化的，可以在上述步骤增加一个目标函数M，即新增m个颜色。本问即是多目标寻优问题。可以去看下之前我发的推文(推文路径：算法-优化算法-智能优化算法函数寻优补充篇)，专门举了自变量个数变化的寻优案例程序，以及多目标常用排序方法(推文路径：算法-优化算法-非支配排序-Ⅱ)，就自己去微信公众号找推文了。

 

 

B 题 技术问答社区重复问题识别

 

之前发的词云图推文可以参考下字符串处理(推文路径：算法-Matlab版-词云图)，本题的基本步骤为：字符串处理(建议以翻译列的问题来做，这些问题数据是爬虫下来的，会有很多干扰字符串，将换行符、网址、表情、图片字符删掉，在是对一些标点符号、数字进行清理，这里暂时不用清理英文字母)，词汇分割(常用中文词汇库，例如jieba，英文词库可以自己组建一个以软件名称为主的词库，中文词库和英文词库分别进行分词)将每个问题提取成若干个词汇、判断是否为同类问题(这里需要根据附件2训练下模型参数，在训练前需要挖掘一些指标，label列为1的样本例如共同词汇在第1个问题中的占比、共同词汇在第二个问题中的占比，label列为0的，这里要注意看下是否在找出与其共同词汇占比最大的一个问题同样的提取出共同词汇占比数据[这里是为了尽可能将同类和不同类区分开来]，构建好训练集，将训练数据带入到逻辑回归、神经网络、svm等模型中训练参数)。

 

 

 

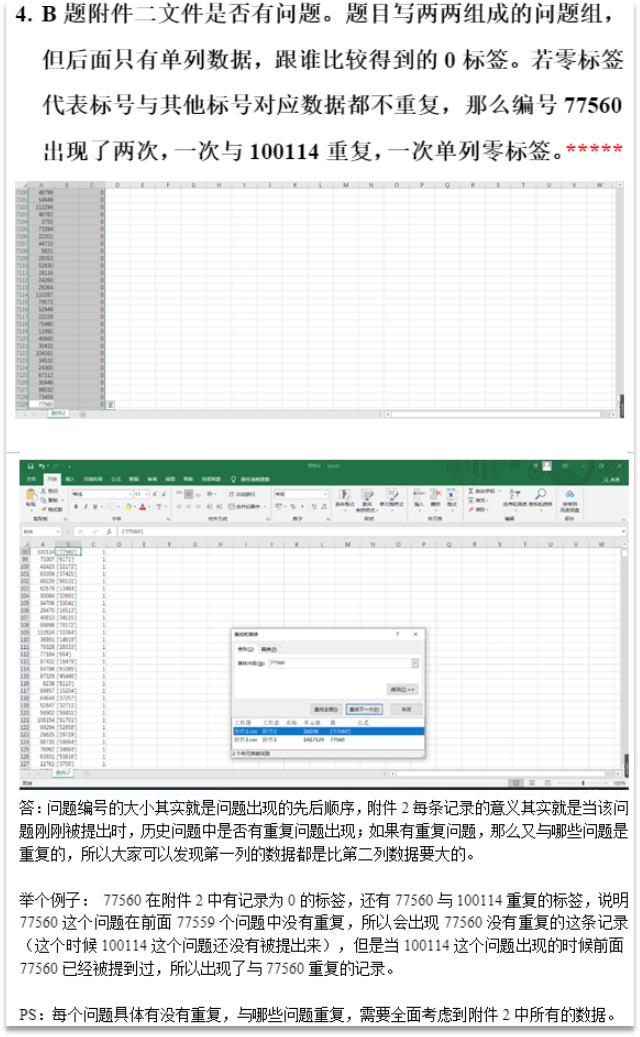
上述为举办方答疑

 

第一问的样本问题组是指附件1中的所有数据，即需要计算出每个问题与其他问题的重复概率。第二问的目标问题是指在第一问的基础上，找到每个问题重复概率排名前十的问题，找出来后通过评估公式进行评估。

 

本题做的效果取决于词库和分词方法，附件中主要是一些软件操作的问题，可以从搜狗万能词库里下载一些软件类的专业词汇包括英文词汇。本题的结果主要依赖词库，如果结果不是很好，就重新组合下词库，也可以从附件问题中挖掘出一些专业词汇添加到词库中。

 

这个问题思路很简单，但是做起来繁琐，一般的都是针对专门的领域构建专门的词库，会花费很大的时间和精力，因此本题结果能看过得去就行。