2021华东杯数学建模赛题思路

Posted 2021-06-06 微信公众号：您好啊数模君

​A机器人扔瓶子

 

机器人扔瓶子大赛 由瓶子引发的科技狂欢TsinghuaJoking-CSDN博客

https://blog.csdn.net/zhuoqingjoking97298/article/details/112610921?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161982743916780274163045%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=161982743916780274163045&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-112610921.first_rank_v2_pc_rank_v29&utm_term=%E6%9C%BA%E5%99%A8%E4%BA%BA%E6%89%94%E7%93%B6%E5%AD%90&spm=1018.2226.3001.4187

 

其实不管怎么去设计机器人，设计的结果就是出手后的重心速度运动方向、主轴竖直方向的夹角、加速度和向心加速度，向心加速度这里又要分出手时旋转中心是瓶口还是瓶底，一般是瓶口，瓶子不是圆球，质量分布不一样。让它以精准的姿态落在平台上，需要考虑流体动力学、抛射物体运动、向心力、重力等因素。平台与机器人出手高度差自行设置，如果是考虑空瓶，就不用考虑流体力学，就是简单的一个抛物线和是否在触碰平台时瓶身的主轴是否近似平台的垂线，这里的近似有一个容差范围，一般不会超过最高点到落地点直线与竖直方向上的夹角。如果是要考虑瓶内装了多少质量的水。在抛物过程中，向心加速度会动态改变，重心也会实时发生变化，在液体在瓶内下落过程也伴随着总质量的相对减少。本题程序设计可以写一个启发式算法，自变量为出手时的重心速度方向竖直方向上的夹角和加速度、主轴竖直方向的夹角、向心加速度四个指标，目标函数就是最后落地主轴竖直方向上的夹角，求最小，约束条件有各自变量范围和落地后主轴竖直方向上的夹角容差。平台高度，机器人到平台中心距离等自行设置。本题思路是优化，但是主体还是抛物仿真，相关角动量守恒、流体力学请参阅专业文献。求解过程就按每单位时间点的状态去推演瓶子的状态参数（例如向心加速度、重心位置、重心速度大小和方向以及加速度等）就可以了，时间间隔可以设为0.01-0.05s。

 

B建立新冠病毒群体免疫屏障

 

先说说全球实时数据，给两个网址

https://ourworldindata.org/coronavirus-data?country=

红圈部分可以选择国家，然后点击下载，google浏览器亲测可下载

  

 

 

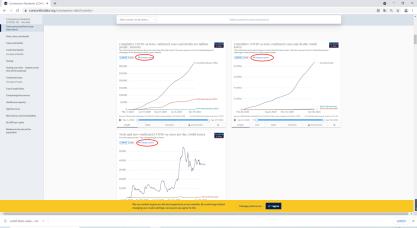
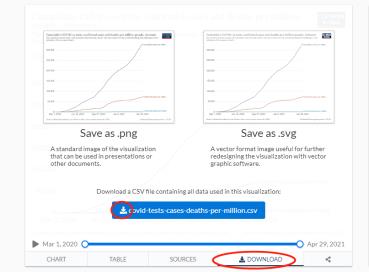
如果上个网址不行，可以尝试下面这个网址，虽然不支持数据下载，但是可以直接通过matlab或者python直接读取静态网页数据，然后通过正则表达式处理下。打开右边网页代码方式，右键-检查/审查元素，点击右上方小箭头指向数据，后边会直接找到对应的代码段，看下对应的字符串，用正则表达读取出数据就行

 

 

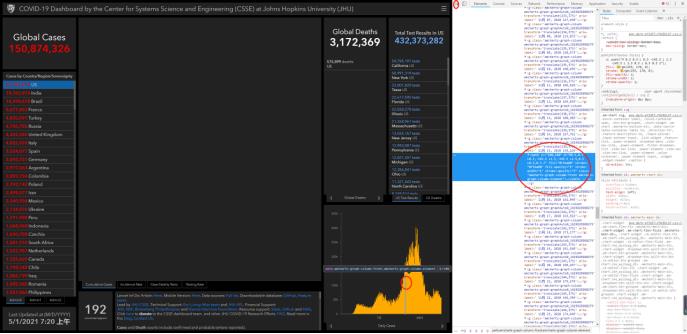
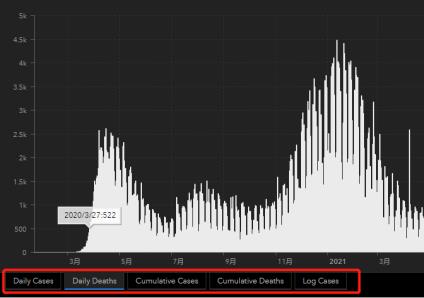
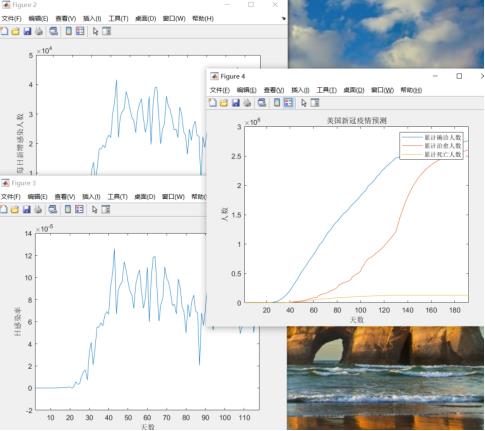
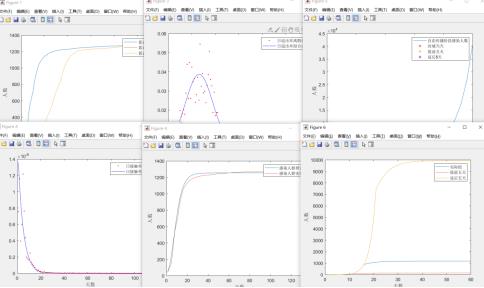
这道题用SIR就行，考不考虑隔离已经对于美国来说不存在了，用SEIR模型也可以，但是意义不是很大。下面是我做过的新冠疫情一些案例，案例程序请私信微信公众号后台或者加q群322273643

 

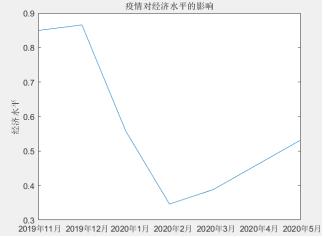
这道题中说到的免疫屏障疫苗最终呈现就是降低感染率，病毒变异则是增加感染率，降低治愈率，这些通过设置过程参数在模型中体现就可以，疫苗接种率的作用，可以通过设置不同接种率，体现出对感染率的影响，做个灵敏度分析；在此基础上考虑病毒变异，前者是降低感染率，后者则是直接影响到疫苗的作用效果，疫苗作用效果就是降低感染率，病毒的变异一方面折损疫苗对降低感染率和提高治愈率的影响，一方面直接增加病毒的感染率。免疫屏障和物理隔离对于整个社会的代价及收益的异同，这里对社会的影响主要还是经济的影响，可以到金十数据网上下载实时的经济数据，量化经济水平，然后利用目前疫情状况（选出疫情比较重要的指标）求与经济水平的关系式，然后在与采取免疫屏障和物理隔离后预估的疫情情况去计算出改善后的经济水平，前后对比下，说一下免疫屏障和物理隔离措施是有用的就可以了。第一问的话就用全球疫情来做分析，第三问在单独做美国疫情的分析。

 

第二问免疫屏障主要看的是接种率，去查一下看有没有城市一直在公布接种率的就选哪个城市，这里的免疫屏障，以目前中国疫情状况，本地感染的基本没有，主要是外来输入病例，外来病例可能会带有变异病毒，这道题没有具体的思路可以说，可以这么来做，当（1-接种率）<感染率*（1+变异率），构建类似的公式即可，最后给出一个时间结果就行

 

第三问就用第一问的模型，模型中的参数就通过美国疫情数据去求，然后随时间推演美国疫情的发展，特别注意疫苗是在某个时刻加入进去的，疫苗接种对感染率和治愈率的影响也是从此刻开始的。

 

 

C布线问题

 

先说下问题背景，一个电子零部件可以有很多层电路板叠加一起的，只要能连通相应接口即可，一二问主要有一下三种连接方式：直接连接、一次转弯连接、多次转弯连接

 

 

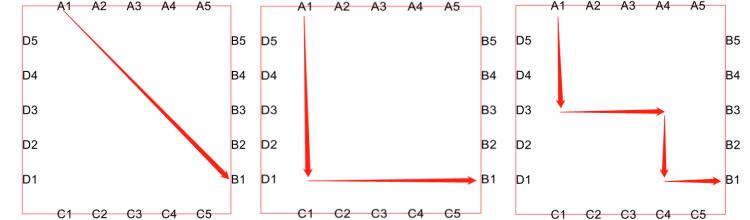
C题就说说程序设计思路吧，每个问都是约束条件不一样而已，C题是优化设计问题，但是用优化算法做的意义也不是很大，但可以凑字数

 

 

1.一块电路板上会有数条连线，切记这里可不是对各连线分组哈，自变量通过randperm产生上述连线的依次排布。这里的序列和遗传算法的染色体比较相似，可以直接嵌套遗传算法，只不过要更改下交叉变异函数，这是自定义函数案例，参考下。用randperm函数产生M个个体。

 

function x=jiaocha(x,a)

if nargin < 2

    a=0.3;%未设置交叉率则默认为0.3

end

y=x(end:-1:1);

b=randperm(length(x));

if rand<a   %随机1/3个位置进行交叉互换

    x(b(1:fix(length(x)/3)))=y(b(1:fix(length(x)/3)));

end

 

function selchrom=bianyi(selchrom,n,a)

if nargin < 3

    a=0.5;%未设置变异率则默认为0.5

end

for i=1:length(selchrom)

    if rand<a

        b=randi(n);

        c=find(selchrom==b);

        d=selchrom(i);

        selchrom(i)=b;

        selchrom(c)=d;

    end

end

 

2.对每个个体的线路进行排布

构造有向矩阵，初始矩阵都是1，图1可以看作是7*7矩阵

While 直到所有线路都已安排，否则：

for循环(执行k次模拟排布，直到下一组初始和终止端口无法安排则终止，保留当前结果，初始化矩阵[更换一张新的电路板])

按照序列依次选出需要连接的初始和终止端口

每个个体会从随机从三种连接方式选出一种，通过的整列位置改为1(第一问是不允许交叉点，如果是允许一个交叉点，那么就把初始矩阵赋值为2)

无法安排下一端口组合则终止循环

记录当前电路板排布

end并选出排布端口组合最多的排布结果

end并记录使用电路板数

保存每个个体结果

 

3.按正常遗传交叉变异过程

 

后面的问题就是在上述设计思路上添加约束条件，程序不难，外循环为遗传算法，内循环则是进行k次蒙特卡洛实验。